7.3　频率特性的表示方法

频域法作为一种图解分析方法，采用图形化的工具来对系统进行分析。频率特性曲线包括三种常用形式：极坐标图（又称乃奎斯特图、乃氏图或Nyquist图）、对数坐标图（又称对数频率特性曲线或Bode图）、对数幅相图（又称对数幅相频率特性曲线或Nichols图）。

7.3.1　极坐标图（Nyquist图）

系统频率特性可表示为：

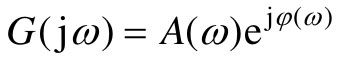
用向量表示某一频率ωi下的G(jωi)向量的长度A(ωi)，向量极坐标角为φ(ωi)，φ(ωi)的正方向取为逆时针方向，选极坐标与直角坐标重合，极坐标的顶点在坐标原点，如图7.2所示。

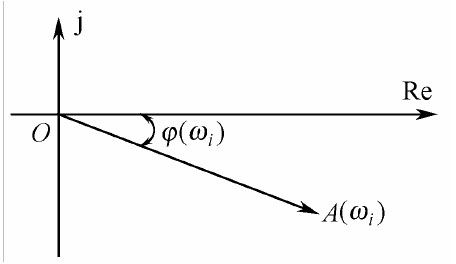
图7.2　极坐标图

频率特性G(jω)是输入频率ω的复变函数，是一种变换。当频率ω由0→∞时，G(jω)变化的曲线，即向量端点轨迹，就称为极坐标图。

极坐标图中，当ω=ωi时，在实轴上的投影即为实频特性p(ωi)，在虚轴上的投影即为虚频特性。

7.3.2　对数坐标图（Bode图）

Bode图由对应对数幅频特性和对应对数相频特性的两张图组成，如图7.3所示。

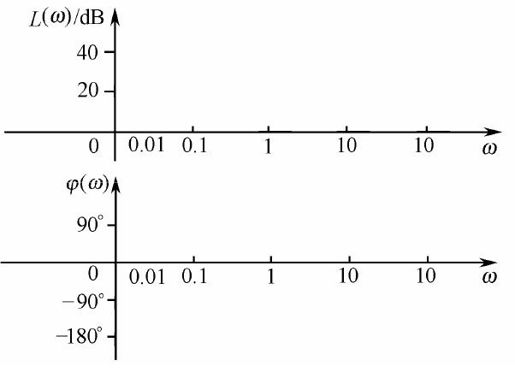
图7.3　对数坐标图

对数幅频特性是频率特性的对数值L(ω)=20lgA(ω)与频率ω的关系曲线；对数相频特性是频率特性的相角φ(ω)与频率ω的关系曲线。

对数幅频特性的纵轴为L(ω)=20lgA(ω),单位为dB（分贝），采用线性分度，A(ω)每增加10倍，L(ω)增加20 dB；横坐标采用对数分度，即横轴上的ω取对数后为等分点。

对数相频特性横轴采用对数分度，纵轴为线性分度，单位为°（度）。

Bode图的优点可概括如下：

（1）将幅值相乘化为对数相加运算，大大简化了系统频率特性的绘制工作。

（2）由于横轴采用了对数分度，缩小了比例尺，从而扩大了频率视野，可以在较大的频段范围内表示系统频率特性。在一张Bode图上，既画出了频率特性的中、高频段，又能清楚地画出其低频段，在分析和设计系统时，低频段特性也是非常重要的。

（3）可以绘制渐近的对数幅频特性；也可以制作标准样板，画出精确的对数频率特性。

7.3.3　对数幅相图（Nichols图）

对数幅相图也称Nichols图，它是将对数幅频特性和相频特性两张图在角频率为参变量的情况下合成为一张图，如图7.4所示。其特点是纵轴为L(ω)=20lgA(ω)，单位为dB（分贝），采用线性分度；横坐标采用对数分度，单位为°（度），频率ω为参变量。

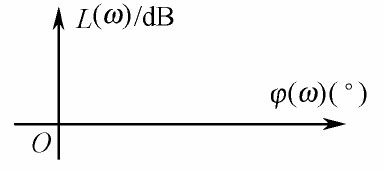
图7.4对数幅相坐标系

7.3.4　典型环节的频率特性

控制系统由若干典型环节组成，常见的典型环节有比例环节、惯性环节、积分环节、微分环节、比例微分环节、振荡环节和滞后环节等。下面分别讨论典型环节的频率特性。

1. 比例环节

比例环节的传递函数为G(s)=K。

比例环节的幅相频率特性为：

比例环节的幅频特性、相频特性均与频率ω无关，因此，当ω由0→∞时，幅频特性A(ω)是实轴上的一点，相频特性φ(ω)=0°表示输出与输入同相位。

比例环节的对数频率特性为：

比例环节的对数幅频特性L(ω)表现为平行于横轴的一条直线，相频率特φ(ω)=0°相当于相频特性的横轴。

1. 惯性环节

惯性环节的传递函数为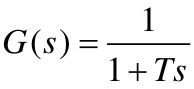，其中T为环节的时间常数。

惯性环节的幅相频率特性为：

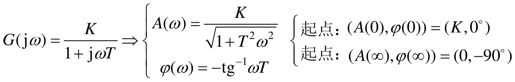
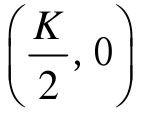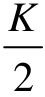可以证明，惯性环节的幅相特性是个圆心在，半径为的下半圆。

惯性环节的对数频率特性为：

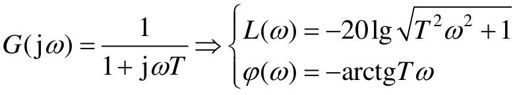
惯性环节的对数幅频特性L(ω)曲线近似为两段直线，在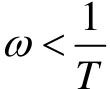时是零分贝线，在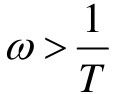时是一条斜率为-20 dB/dec的直线。两直线相交，交点处频率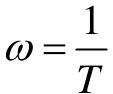，称为转折频率。两直线实际上是对数幅频特性曲线的渐近线，故又称为对数幅频特性渐近线。

1. 积分环节

积分环节的传递函数为。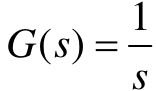

积分环节的幅相频率特性为：

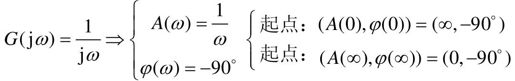
积分环节的幅频特性为负虚轴。

积分环节的对数频率特性为：

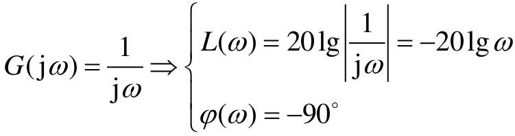
积分环节的对数幅频特性L(ω)曲线是一条斜率为-20 dB/dec的直线，在ω=1这一点穿过零分贝线。相频率特-(ω)=-90°，与频率无关，是一条平行于横轴的直线。

1. 微分环节

微分环节的传递函数为G(s)=s。

微分环节的幅相频率特性为：

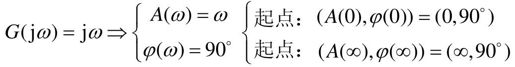
微分环节的幅频特性为正虚轴。

微分环节的对数频率特性为：

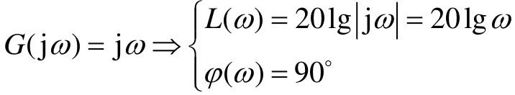
微分环节的对数幅频特性L(ω)曲线是一条斜率为+20 dB/dec的直线，在ω=1这一点穿过零分贝线。相频率特φ(ω)=90°，与频率无关，是一条平行于横轴的直线。

1. 二阶振荡环节

二阶振荡环节的传递函数为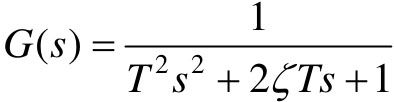，其中T为时间常数，ζ为阻尼比。

二阶振荡环节的幅相频率特性为：

二阶振荡环节的对数频率特性为：

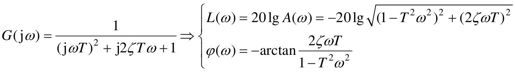
二阶振荡环节的对数相频率特在低频段近似为L(ω)=0的一条直线，这条直线与横坐标重合；在高频段近似为一条斜率为-40 dB/dec的直线。

在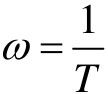附近，对数幅频特性将出现谐振峰值Mp，其大小与阻尼比有关。

1. 滞后环节

滞后环节的传递函数为G(s)=e-τs，其中τ为滞后时间。

滞后环节的幅相频率特性为

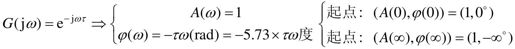
滞后环节的幅相特性是一个以原点为圆心，半径为1的圆。

滞后环节的对数频率特性为：

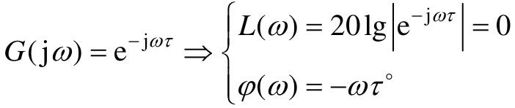
滞后环节的对数幅频特性L(ω)曲线是一条与0dB重合的直线。相频率特φ(ω)曲线随着ω的增大而减小。