7.2　频率特性基本概念

采用频率特性作为数学模型来分析和设计系统的方法称为频率特性法，又称为频率响应法。频率响应法的基本思想是把控制系统中的各个变量看成一些信号，而这些信号又是由许多不同频率的正弦信号合成的；各个变量的运动就是系统对各个不同频率的信号的响应的总和。

这种观察问题和处理问题的方法起源于通信中的音频信号传播，各种音频信号（电话、电报）信号都被看做由不同频率的正弦信号成分合成的，并按此观点进行处理和传递。20世纪30年代，这种观点被引进控制科学，对控制理论的发展起了强大的推动作用。它克服了直接用微分方程研究系统的种种困难，解决了许多理论问题和工程问题，迅速形成了分析和综合控制系统的一整套方法。

频率分析法是根据频率特性曲线的形状及其特征量来分析研究系统的特性，而不是对系统模型求解，它是以传递函数为基础的又一种图解法，它同根轨迹法一样卓有成效地用于线性定常系统的分析和设计。

频率分析法有着重要的工程价值和理论价值，应用十分广泛，频域方法和时域方法同为控制理论中两个重要方法，彼此互相补充，互相渗透。

7.2.1　频率特性定义

频率特性是指系统在正弦信号作用下，稳态输出与输入之比相对频率的关系特性。频率特性函数与传递函数有直接的关系，记为：

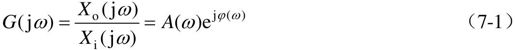
式中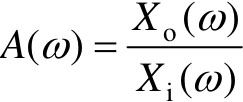，称为幅频特性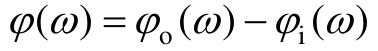，称为相频特性。

频率特性还可表示为：

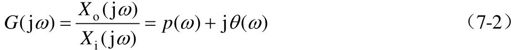
式中，p(ω)为G(jω)的实部，称为实频特性；θ(ω)为G(jω)的虚部，称为虚频特性。

显然

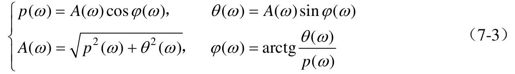
需要注意的是，当输入为非正弦的周期信号时，其输入可利用傅里叶级数展开成正弦波的叠加，则其输出为相应的正弦波的叠加。此时系统频率特性定义为系统输出量的傅氏变换与输入量的傅氏变换之比。

7.2.2　频域分析法的特点

从前面章节可知，微分方程可以比较准确地反应控制系统的运动本质。时域分析法是直接对微分方程求解，具有物理概念强、系统动态特性曲线直观的优点。但对于高阶系统，求解特征方程的根比较困难，计算工作量因系统阶次升高而加大，而且不易分析出各部分对系统总体动态性能的影响，难以找出主要因素；在设计系统校正环节时更为不便；尤其是在工程中，需要比较简单而直观的作图法来反应系统性能的主要特征。这正是时域法的不足，而根轨迹法和频率分析法则正是满足这些要求的工程方法，至今仍是控制理论中极为重要的基本方法。

频域法的主要特点可归纳如下：

（1）适用于各环节、开环和闭环系统的性能分析。运用奈奎斯特稳定判据，通过作图方法，可以根据系统开环频率特性分析闭环系统的稳定性及性能，而不必求解出系统的特征根，从而避免了直接求解微分方程的困难。

（2）频率特性有明确的物理意义。很多元部件频率特性都可用实验方法确定，特别是对于机理复杂或机理不明而难以列写微分方程的元部件或系统，在实验室中采用信号发生器和一些精密测量仪器，可以测出其频率特性，因此在工程上有着广泛的应用。

（3）频域性能指标和时域性能指标有确定的对应关系。对于二阶系统，频率特性与时域过渡过程性能指标有确定的对应关系；对于高阶系统，通过把系统参数和结构的变化与时域过渡过程指标联系起来，两者间也存在着近似的对应关系。

（4）频域设计可兼顾动态响应和噪声抑制两方面的要求。当系统在某些频率范围内存在严重的噪声时，应用频域分析法可以设计出能满意地抑制这些噪声的系统。

（5）在校正方法中，频域分析法校正最为方便。当系统的性能指标以幅值裕度、相位裕度和误差系数等形式给出时，采用频域分析法来分析和设计系统很方便。

（6）频域法不能全面分析非线性系统。频域法主要应用于单输入单输出的线性定常系统的分析研究中，在多输入多输出的线性定常系统中也有应用。但在非线性系统中只有某些局部而典型的应用，它不能对非线性系统进行全面的分析。从根本上说它不可能成为研究和设计非线性控制系统的得力工具，这正是它主要的局限性。

7.2.3　频域性能指标

与时域响应中衡量系统性能采用时域性能指标类似，频率特性在数值上和曲线形状上的特点通常可用频域性能指标来衡量，它们在很大程度上能够间接地表明系统动静态特性。系统频率特性曲线如图7.1所示。

图7.1　频率特性曲线

常见的频域性能指标主要有：

（1）谐振频率ωr，表示幅频特性A(ω)出现最大值时所对应的频率。

（2）谐振峰值Mr，表示幅频特性的最大值，Mr值大表明系统对频率的正弦信号反应强烈，即系统的平稳性差，阶跃响应的超调量大。

（3）频带ωb，表示幅频特性A(ω)的幅值衰减到起始值的0.707倍时所对应的频率。ωb大表明系统复现快速变化信号的能力强，失真小，即系统快速性好，阶跃响应上升时间短，调节时间短。

（4）零频A(0)，表示频率ω=0时的幅值。A(0)表示系统阶跃响应的终值，A(0)与1之间的差反映了系统的稳态精度，A(0)越接近1，系统的精度越高。