10.2　状态反馈与极点配置

与经典控制理论一样，现代控制系统中仍然主要采用反馈控制结构，但不同的是，经典控制理论中主要采用输出反馈，而现代控制系统中主要采用内部状态反馈。状态反馈可以为系统控制提供更多的信息反馈，从而实现更优的控制。

闭环系统极点的分布情况取决于系统的稳定性和动态品质，因此，可以根据对系统动态品质的要求，规定闭环系统的极点所应具备的分布情况，把极点的布置作为系统的动态品质指标。这种把极点布置在希望的位置的过程称为极点配置。在空间状态法中，一般采用反馈系统状态变量或输出变量的方法来实现系统的极点配置。

10.2.1　状态反馈

状态反馈是将系统的内部状态变量乘以一定的反馈系数（矢量），然后反馈到系统输入端与系统的参考输入综合，综合而成的信号作为系统的输入对系统实施控制。

控制系统结构如图10.1所示，实线部分表示原来系统∑(A,B,C,D)的结构图，其动态方程为

P_286-1

当加上图10.1中虚线所示的状态反馈环节后，其中的线性状态反馈控制律为

P_286-2

式中，R是参考输入，K称为状态反馈增益矩阵，为p×n矩阵。

系统动态方程变为

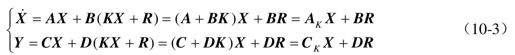
P_287-1

式中，AK=A+BK，CK=C+DK，当D=0时，状态反馈系统闭环传递函数WK(s)为

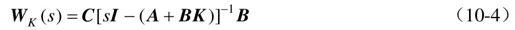
P_287-2

式中，A+BK为闭环系统的系统矩阵。

从式（10-1）和式（10-3）可以看出，状态反馈前后的系统矩阵分别为A和A+BK，特征方程分别为det[λI-A]和det[λI-(A+BK)]，可看出状态反馈后的系统特征根（即系统的极点）不仅与系统本身的结构参数有关，而且与状态反馈K有关。应该指出完全能控的系统经过状态反馈后，仍是完全能控的，但状态反馈可能改变系统的能观性，即原来可观的系统在某些状态反馈下，闭环可以是不可观的。同样，原来不可观的系统在某些状态反馈下，闭环可以是可观的。状态反馈是否改变系统的可观测性，要做具体分析。

状态反馈后的控制系统∑K(AK，B，CK，D)其系统维数不变，但系统矩阵AK及系统输出矩阵CK随反馈环节K而改变。通过调整K可以改善系统的稳定性、快速性、稳定误差，以及系统可观性与可控性，这也是后面利用状态反馈对极点进行配置的依据。

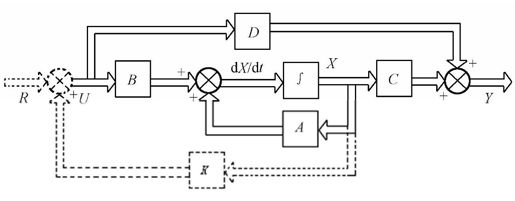
P_287-3

图10.1　状态反馈控制结构图

10.2.2　输出反馈

把系统的输出变量按照一定的比例关系反馈到系统的输入端或H_287-1端称为输出反馈，如图10.2所示。由于状态变量不一定具有物理意义，所以状态反馈往往不易实现；而输出变量则具有明显的物理意义，因此输出反馈比较容易实现。

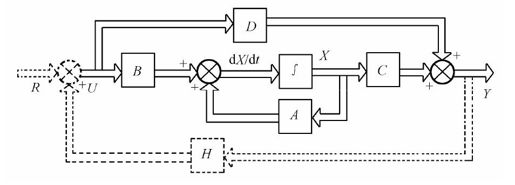
P_287-4

图10.2　输出反馈控制结构图

输出反馈是采用输出矢量Y构成反馈信号综合到系统的控制输入端，以改善系统的各项性能。实线部分表示原来系统∑(A,B,C,D)，虚线部分表示加上输出反馈环节H后形成的输出反馈。输出反馈的控制信号为：

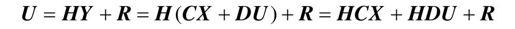
P_288-1

化简可得

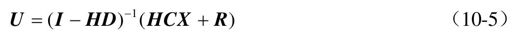
P_288-2

将式（10-5）代入式（10-1）所代表的原系统动态方程，可得

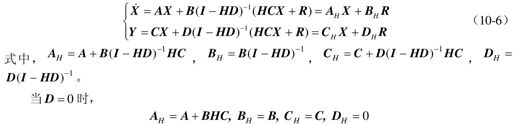
P_288-3

输出反馈系统闭环传递函数WH(s)为

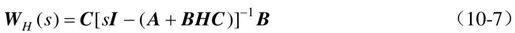
P_288-5

式中，(A+BHC)为闭环系统的系统矩阵。

从式（10-1）和式（10-6）可以看出，输出反馈前后的系统矩阵分别为A和A+BHC，特征方程分别为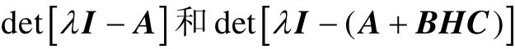H_288-1，可看出状态反馈后的系统特征根（即系统的极点）不仅与系统本身的结构参数有关，而且与输出反馈矩阵H有关。也就是说，输出反馈H改变了原系统的系统矩阵A，从而改变了系统稳定性（改变了系统的特征根）、系统可控性（改变了可控判别阵M）和系统可观性（改变了可观判别矩阵N）。

比较式（10-4）和式（10-7）可知，输出反馈系统中的HC相当于状态反馈中的K。但由于H是r×m阶矩阵，而K是r×n阶矩阵（其中r是系统输入维数，m是输出维数，n是状态维数），且通常情况下n>m，因此状态反馈一般能提供更多的系统反馈信息，从而带来更优的控制效果。

从上面的分析中可以归纳出状态反馈与输出反馈的如下基本特点：

（1）两种形式反馈的重要特点是反馈的引入并不增加新的状态变量，即闭环系统和开环系统具有相同的阶数。

（2）两种反馈闭环系统均能保持反馈引入前的能控性，而对于反馈闭环系统的能观性则不然。对状态反馈，闭环后不一定能保持系统的能观性；而对输出反馈，闭环后必定能保持系统的能观性。

（3）在工程实现方面，两种反馈形式都会遇到一定的困难。

（4）输出反馈的一个突出优点是工程上构成方便，但事实证明，状态反馈比输出反馈具有更好的特性。对具体系统而言，要从实际出发进行具体分析与选择。

10.2.3　极点配置

动力学的各种特性或各种品质指标，在很大程度上是由系统的极点决定的，因此系统设计的一个重要目标是在S平面上设计一组系统所希望的极点。

所谓极点配置问题，就是通过反馈矩阵的选择，使闭环系统的极点，即闭环特征方程的特征值恰好处于所希望的一组极点位置上。由于希望的极点具有一定的任意性，因此极点的配置也具有一定的任意性。

状态反馈和输出反馈（主要指输出反馈至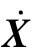H_289-1的情况）都能够对系统进行极点配置，且一般认为用简单的比例反馈就能使问题得到解决。

极点配置是通过选择一个状态反馈矩阵，使闭环系统的极点处于期望的位置上。在状态空间中，极点任意配置的充分必要条件是系统必须是完全状态可控的。

极点配置方法如下所述：如果系统是完全状态可控的，那么可选择期望设置的极点，然后以这些极点作为闭环极点来设计系统，利用状态观测器反馈全部或部分状态变量，使所有的闭环极点均落在各期望位置上，以满足系统的性能要求。这种设置期望闭环极点的方法就称为极点配置方法。

在极点配置方法中，为使全部的闭环极点位于期望的位置上，需要反馈全部的状态变量。但在实际系统中，不可能测量到全部的状态变量，为了实现状态反馈，利用状态观测器对未知的状态变量进行估计是十分必要的。

设给定的线性定常系统为

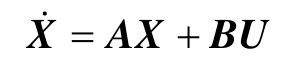
P_289-1

式中，X为n维状态向量；U为p维状态向量；A和B为相应维数的常数阵。若给定n个反馈性能的期望闭环极点为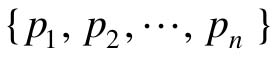：H_289-2，则极点配置的设计问题就是确定一个p×n状态反馈增益矩阵K，使状态反馈闭环系统的极点为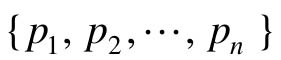H_289-3，即

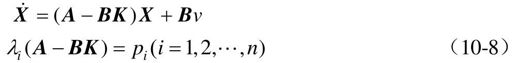
P_289-2

式中，λi(•)表示(•)的特征值。

10.2.3.1　单输入单输出系统的极点配置

对于单输入单输出的n阶系统，其反馈增益矩阵K是一行向量，仅包含n个元素，可由n个极点唯一确定。反馈增益矩阵K由期望的闭环极点确定，而期望的闭环极点根据闭环系统的设计要求决定，如对响应速度、阻尼比、带宽等的要求。

设已知系统为∑(A,b)，期望的闭环极点为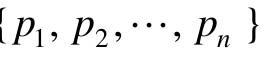H_289-4，要确定1×n的反馈增益矩阵K，使得K满足式（10-8）。

单输入、单输出系统极点配置方法设计步骤如下：

（1）确定受控系统∑(A,b)完全可控，如果系统不是完全可控，则不能进行极点配置，并确定系统开环特征多项式det(sI-A)。

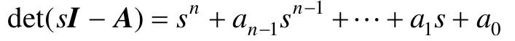
P_289-3

（2）由希望的闭环极点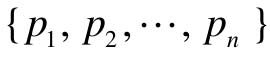H_289-5计算闭环期望的特征多项式。

P_289-4

（3）计算

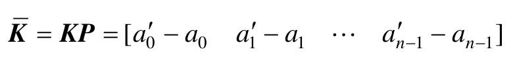
P_289-5

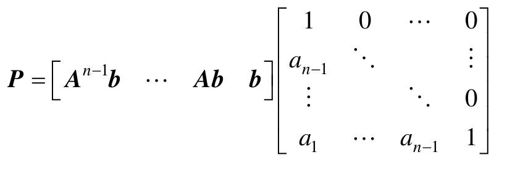
（4）计算变换矩阵P及其逆P-1。

P_289-6

（5）将所求出的状态反馈增益阵转换成实际实施的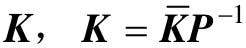H_290-1。

10.2.3.2　多输入、多输出系统的极点配置

对于多输入多输出系统的极点配置，有多种算法可以确定状态反馈增益矩阵，但与单输入、单输出系统相比，则要复杂得多。在多变量系统中，状态反馈增益矩阵K不是唯一的，如果要确定唯一的极点，则必须附加其他条件，但从工程应用角度来说，希望K的各个元素尽可能小。

多输入、多输出系统∑(A,B)极点配置方法设计步骤如下所述：

（1）将能控矩阵对{A,B}转化成某种规范型（如龙博格规范型）；

（2）将给定的期望闭环极点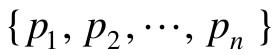H_290-2按规范型H_290-3计算它们的特征多项式；

（3）求取规范型的状态反馈增益阵K。

10.2.3.3　极点配置的注意问题

使用极点配置方法时，要注意以下问题：

（1）系统完全状态可控是求解的充分必要条件；

（2）应把闭环系统的期望特性转化为极点位置；

（3）理论上，选择反馈增益可使系统有任意快的时间响应。加大反馈增益可提高系统的频带、加快系统的响应。但过大的反馈增益，在有一定误差信号时，将会导致控制信号无限增大，这在工程上是无法实现的，因此必须考虑到反馈增益物理实现的可能性。

（4）当系统的阶次较高时，可用Ackerman公式，通过计算机求解。

10.2.4　MATLAB/Simulink在极点配置中的应用

利用MATLAB控制系统工具箱中的place()或acker()函数，可以容易求出全状态反馈闭环系统的反馈矩阵，使系统极点配置在所希望的位置上。下面分别对这两个函数进行介绍。

（1）place( )函数。place( )函数是基于鲁棒极点配置的算法编写的，用来求取状态反馈阵K，使得多输入系统具有指定的闭环极点p，即p=eig(A-B·K)。

place( )函数常用的调用格式为

  1. K=place(A,B,p)
  2. [K,prec,message]=place(A,B,p)

其中，（A,B）为系统状态方程模型，p为包含期望闭环极点位置的列向量，返回变量K为状态反馈行向量。prec为闭环系统的实际极点与期望极点p的接近程度，prec中的每个量的值为匹配的位数。如果闭环系统的实际极点偏离期望极点10%以上，那么message将给出警告信息。

需要注意的是：函数place( )不适用于含有多重期望极点的配置问题。

（2）acker( )函数。acker( )函数是根据Ackerman公式编写的，Ackerman公式如下所述。

若单输入系统是可控的，那么反馈矩阵K可由式（10-9）求得。

采用的状态反馈规律为u=r+Kx，则反馈矩阵K为

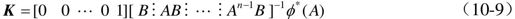
P_290-1

φ(s)是状态观测器的期望特征多项式，即

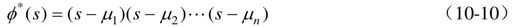
P_290-2

式中，μ1, μ2, …, μn是期望的特征值，φ*(A)为

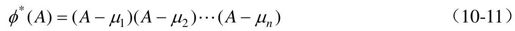
P_291-1

acker( )函数常用的调用格式为

  1. K=acker(A,B,P)

其中，(A,B)为系统状态方程模型，p为包含期望闭环极点位置的列向量，返回变量K为状态反馈行向量。

需要注意的是：acker()只适用于单输入系统，希望的极点可以包括多重极点（位于同一位置的多个极点）。

下面通过实例讲述采用MATLAB/Simulink进行极点配置。

【例10-1】　已知系统的方程为X=AX+BU，其中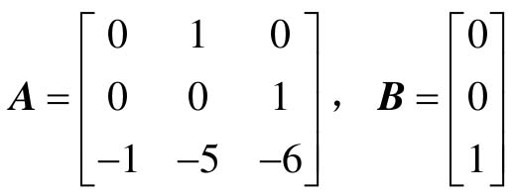H_291-1，试采用状态反馈U=-KX，希望的闭环极点为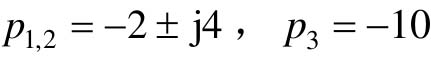H_291-2，试用MATLAB确定状态反馈增益矩阵，并计算当系统初始条件为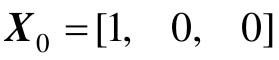H_291-3时的响应。

解：MATLAB程序代码如下。

  1. A=[0, 1, 0; 0, 0, 1; -1, -5, -6];  B=[0; 0; 1]    %状态矩阵A和输入矩阵B
  2. P=[-2+j*4, -2-4*j, -10]          %希望配置的极点
  3. K=acker(A, B, P)              %采用Ackerman公式法进行极点配置
  4. sys_new=ss(A-B*K, eye(3), eye(3), eye(3))    %极点配置后的新系统
  5. t=0:0.1:4         %仿真时间
  6. X=initial(sys_new, [1; 0; 0], t)      %初始条件为X0=[1,0,0]时的零输入响应
  7. x1=[1, 0, 0]*X' ;  x2=[0, 1, 0]*X';  x3=[0, 0, 1]*X'; %状态x1、x2、x3
  8. subplot(3, 1, 1)         %将状态x1、x2和x3的零输入响应绘制在同一个图形窗口中
  9. plot(t, x1);   grid         %绘制状态x1的零输入响应并添加栅格
  10. title('零输入响应')        %添加图标题
  11. ylabel('状态变量x1')      %标注纵坐标轴
  12. subplot(3, 1, 2)           %将状态x1、x2和x3的零输入响应绘制在同一个图形窗口中
  13. plot(t, x2) ;   grid         %绘制状态x2的零输入响应并添加栅格
  14. ylabel('状态变量x2')       %标注纵坐标轴
  15. subplot(3, 1, 3)        %将状态x1、x2和x3的零输入响应绘制在同一个图形窗口中
  16. plot(t, x3) ;   grid         %绘制状态x31的零输入响应并添加栅格
  17. xlabel('时间/秒') ;  ylabel('状态变量x3')         %标注横纵坐标轴

运行结果如下：

  1. K=   199    55     8           %状态反馈增益矩阵

由输出结果可知，所求状态反馈增益矩阵K=[199, 55,8]。

零输入响应曲线如图10.3所示。

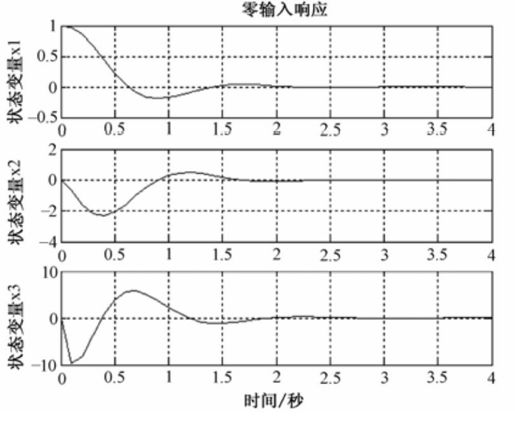
P_292-1

图10.3　3个系统状态的零输入响应曲线

【例10-2】　已知数字控制系统的状态方程为

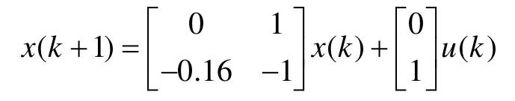
P_292-2

设系统期望的闭环极点为z=0.5±j0.5，现用全状态反馈控制系统，求反馈增益矩阵K。

解：MATLAB程序代码如下。

  1. A=[0, 1; -0.16, -1];  B=[0; 1]            %状态矩阵A和输入矩阵B
  2. P=[0.5+j*0.5, 0.5-0.5*j]     %希望配置的闭环极点
  3. K=acker(A, B, P)             %采用Ackerman公式法进行极点配置

运行结果如下：

  1. K= 0.3400   -2.0000         %状态反馈增益矩阵

由输出结果可知，所求状态反馈增益矩阵K=[0.34,-2]。

【例10-3】　已知如图10.4所示的受控系统，其中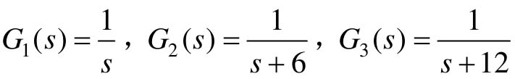H_292-1，状态变量x1, x2, x3如图10.4所示，试对系统进行极点配置，以达到系统期望的指标：输出超调量σp≤5%；超调时间tp≤0.5s；系统频宽ωb≤10；跟踪误差ep=0（对于阶跃输入）、ev≤0.2（对于速度输入），并求极点配置后系统的阶跃响应。

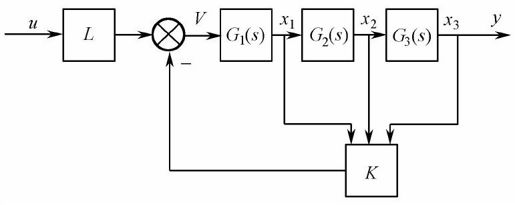
P_292-3

图10.4　例10-3的系统结构图

解：本题通过以下几个步骤进行求解。

【步骤1】　确定受控系统的状态空间模型。

由图可知：H_292-2，把题中的条件代入，得系统的状态方程为

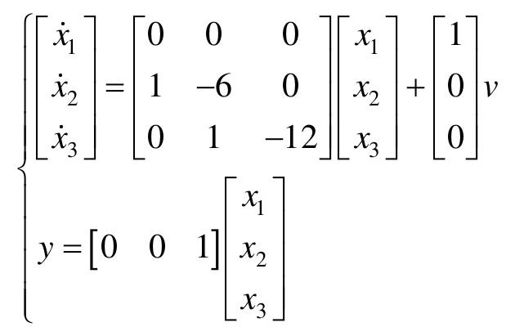
P_293-1

【步骤2】　确定希望的极点。

由于系统是三阶系统，系统有3个极点，可选定其中一对为主导极点，另一个为远极点，系统的性能主要由主导极点决定，远极点对系统的影响不大。

根据二阶系统的关系，先求出主导极点：

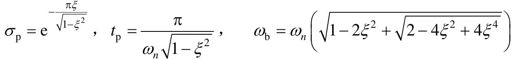
P_293-2

式中，ξ和ωn为此二阶系统的阻尼比和自然频率。

P_293-3

远极点选择使得它和原点的距离大于5|p1|，现取p3=|p1|，因此确定的希望极点为：

P_293-4

【步骤3】　确定状态反馈矩阵K。

MATLAB程序如下：

  1. A=[0, 0, 0; 1, -6, 0; 0, 1, -12] ;   B=[1; 0; 0]      %系统状态矩阵和输入矩阵
  2. P=[-sqrt(2)*5+j*5*sqrt(2), -sqrt(2)*5-j*5*sqrt(2), -100] %希望的极点
  3. K=place(A, B, P)             %采用鲁棒极点配置法进行极点配置

运行结果如下：

  1. K=96.14, -288.3, 6538.          %状态反馈增益矩阵

由输出结果可知，所求状态反馈增益矩阵K为：

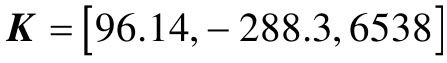
P_293-5

【步骤4】　确定输入放大系数L。

对应的闭环传递函数为H_293-3。

由于系统要求的跟踪阶跃信号误差为0，则

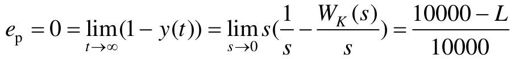
P_293-6

得到放大系数L为：L=10000。

【步骤5】　求极点配置后系统的阶跃响应。

MATLAB的程序如下：

  1. A=[0, 0, 0; 1, -6, 0; 0, 1, -12];    B=[1; 0; 0];    C=[0, 0, 1];    D=0;
  2. P=[-sqrt(2)*5+j*5*sqrt(2), -sqrt(2)*5-j*5*sqrt(2), -100]   %期望配置的极点
  3. K=place(A, B, P)            %采用鲁棒极点配置法进行极点配置
  4. L=10000           %输入放大系数
  5. sys_new=ss(A-B*K, B, C, D)      %极点配置后新系统模型
  6. t=0:0.01:5         %仿真时间
  7. y_new=L*step(sys_new, t)        %求取阶跃响应
  8. plot(, y_new); grid        %绘制阶跃响应曲线并添加栅格
  9. title('极点配置后系统的阶跃响应曲线')       %添加图标题
  10. xlabel('时间/秒');   ylabel('y(t)')         %标注横纵坐标轴

程序运行后，输出结果如图10.5所示。

P_294-1

图10.5　极点配置后系统的阶跃响应曲线