8.4　控制系统校正的根轨迹法

根轨迹法是一种图解法，它描述了系统某一参数（通常是增益）从零变化到无穷大时其闭环极点位置的变化。但在实际中，只调整增益通常是不能获得所希望的性能的，因此，必须改造根轨迹，通过引入适当的校正装置来改变原来的根轨迹。引入校正装置就是在系统中增加零点和（或）极点，通过零/极点的变化改变根轨迹的形状。

用根轨迹法进行校正的基础，是通过在系统开环传递函数中增加零点和极点以改变根轨迹的形状，从而使系统根轨迹在S平面上通过希望的闭环极点。根轨迹法校正的特征是基于闭环系统具有一对主导闭环极点，当然，零点和附加的极点会影响响应特性。

应用根轨迹进行校正，实质上是通过采用校正装置改变根轨迹的，从而将一对主导闭环极点配置到期望的位置上。

在开环传递函数中增加极点，可以使根轨迹向右方移动，从而降低系统的相对稳定性，增大系统调节时间。前面讲的积分控制，相当于给系统增加了位于原点的极点，因此降低了系统的稳定性。

在开环传递函数中增加零点，可以使根轨迹向左方移动，从而提高系统的相对稳定性，减小系统调节时间。前面讲的微分控制，相当于给系统前向通道中增加了零点，因此增加了系统的超调量，并且加快了瞬态响应。

当系统的性能指标是以最大超调量、上升时间、调整时间、阻尼比以及希望的闭环阻尼比、闭环极点无阻尼振频率等表示时，采用根轨迹法进行校正比较方便，在设计系统时，如果需要对增益以外的参数进行调整，则必须通过引入适当的校正装置来改变原来的零极点。

采用根轨迹法确定串联校正参数的条件是：

  • 已确定采用串联校正方案；
  • 给定时域指标σp，ts，ess(∞)。

设已知系统不可变部分的传递函数为：

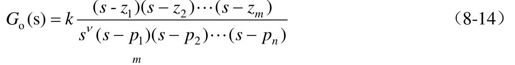
P_222-1

式中，K为开环增益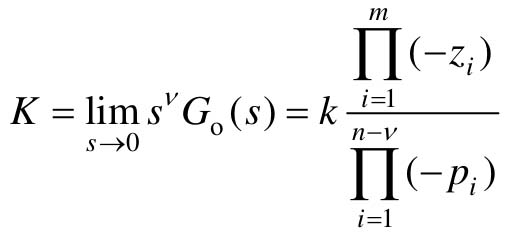，H_0012，开环极点pi(i=1,2,3,…,n-v)和零点zi(i=1,2,3,…,m)为已知数据。

8.4.1　基于根轨迹法的超前校正

用根轨迹法设计超前校正装置的步骤为：

（1）先假定系统的控制性能由靠虚轴最近的一对闭环共轭极点sd来主导。

（2）应用二阶系统参量ζ和ωn与时域指标间的关系，按给定的σp与ts确定闭环主导极点的位置。

（3）绘制原系统根轨迹，如果根轨迹不能通过希望的闭环主导极点，则表明仅调整增益不能满足给定要求，需加校正装置。如果原系统根轨迹位于期望极点的右侧，则应加入超前校正装置。

（4）计算超前校正装置应提供的超前相角。

（5）按式（8-15）求校正装置零点、极点位置。

P_222-2

（6）由幅值条件确定校正后系统增益。

（7）校验系统的性能指标，如果系统不能满足要求指标，适当调整零点、极点的位置。如果需要大的静态误差系数，则应采用其他方案。

8.4.2　基于根轨迹法的滞后校正

用根轨迹法设计串联滞后校正的设计步骤为：

（1）绘制出未校正系统的根轨迹。

（2）根据要求的瞬态响应指标，确定希望的闭环主导极点，根据根轨迹的幅值条件，计算与主导极点对应的开环增益。

（3）按给定的性能指标中关于稳态误差的要求，计算应增大的误差系数值。

（4）由应增大的误差系数值确定校正装置β值，通常β取值不超过10。

（5）确定滞后校正装置的零点、极点。原则是使零点、极点靠近坐标原点，且两者相距β倍。

（6）绘出校正后系统的根轨迹，并求出希望的主导极点。

（7）由希望的闭环极点，根据幅值条件，适当调整放大器的增益。

（8）校验校正后系统各项性能指标，如不满足要求，则适当调整校正装置零点、极点。

8.4.3　基于根轨迹法的超前滞后校正

用根轨迹法设计串联超前滞后校正的设计步骤为：

（1）根据要求的性能指标，确定希望的主导极点sd的位置。

（2）为使闭环极点位于希望的位置，计算超前滞后校正中超前部分应产生的超前相角。

P_223-1

（3）超前滞后校正装置的传递函数为：

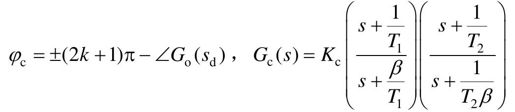
P_223-2

（4）对超前滞后校正中滞后部分的T2选择要足够大，即

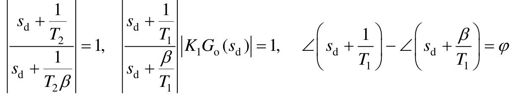
P_223-3

（5）利用求得的β值，选择T2，使

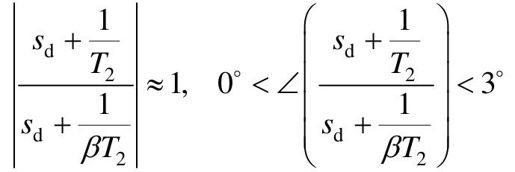
P_223-4

（6）检验性能指标。

8.4.4　MATLAB/Simulink在根轨迹法校正中的应用

根据前面所讲的根轨迹校正设计原则，可以采用MATLAB编写校正函数，调用函数便可设计出所需的校正器，为线性控制系统的设计提供了一种简单有效的途径。下面通过实例介绍用MATLAB实现校正器的根轨迹法设计的详细过程。

【例8-8】　已知系统开环传递函数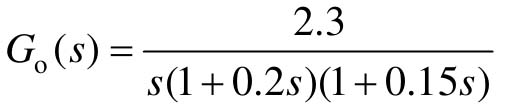H_0013，试设计超前校正环节，使其校正后系统的静态速度误差系数Kv≤4.6，闭环主导极点满足阻尼比ζ=0.2，自然振荡角频率ωn=12.0 rad/s，并绘制校正前后系统的单位阶跃响应曲线、单位脉冲响应曲线和根轨迹。

解：计算串联超前校正环节参数的子函数MATLAB程序代码如下。

  1. %采用根轨迹法设计的串联超前校正的子函数
  2. %G为校正前系统的开环传递函数；Gc为校正环节的传递函数
  3. function Gc=cqjz_root(G, s1, kc)
  4. numG=G.num{1}; denG=G.den{1}
  5. ngv=polyval(numG, s1); dgv=polyval(denG, s1)
  6. g=ngv/dgv
  7. theta_G=angle(g); theta_s=angle(s1)
  8. MG=abs(g); Ms=abs(s1)
  9. Tz=( sin(theta_s)-kc*MG*sin(theta_G-theta_s) )/( kc*MG*Ms*sin(theta_G)
  10. Tp=-( kc*MG*sin(theta_s)+sin(theta_G+theta_s))/(Ms*sin(theta_G))
  11. Gc=tf([Tz, 1], [Tp, 1])

主函数MATLAB代码如下：

  1. num=2.3; den=conv([1, 0], conv([0.2, 1], [0.15, 1]) ); G=tf(num, den)
  2.            %建立校正前系统开环传递函数
  3. zeta=0.2; wn=12.0       %校正后系统的要求性能参数
  4. [num, den]=ord2(wn, zeta)
  5. s=roots(den)
  6. s1=s(1);  kc=2
  7. Gc=cqjz_root(G, s1, kc)
  8. GGc=G*Gc*kc                   %校正后的系统开环传递函数
  9. Gy_close=feedback(G, 1)         %校正前系统的闭环传递函数
  10. Gx_close=feedback(GGc, 1)      %校正后系统的闭环传递函数
  11. figure(1);  step(Gx_close, 'b', 3.5);  hold on
  12.            %绘制校正后系统的单位阶跃响应图
  13. step(Gy_close, 'r', 3.5) ;  grid      %校正前系统的单位阶跃响应
  14. gtext('校正前的');  gtext('校正后的')    %放置曲线的文字注释
  15. figure(2);  impulse(Gx_close, 'b', 3.5);  hold on
  16.            %绘制校正后系统的单位冲激响应图
  17. impulse(Gy_close, 'r', 3.5) ;  grid   %校正前系统的单位冲激响应
  18. gtext('校正前的');  gtext('校正后的')       %放置曲线的文字注释
  19. figure(3);  rlocus(G, GGc);  grid     %绘制校正后系统的根轨迹图
  20. gtext('校正前的');  gtext('校正后的')    %放置曲线的文字注释

运行结果如下：

  1. %超前校正环节传递函数
  2. 1.016 s + 1
  3. ------------
  4. 0.0404 s + 1
  5. %校正后系统闭环传递函数
  6.                      4.672 s + 4.6
  7. -------------------------------------------------------
  8. 0.001212 s^4 + 0.04414 s^3 + 0.3904 s^2 + 5.672 s + 4.

系统校正前后的单位阶跃响应曲线如图8.33所示。

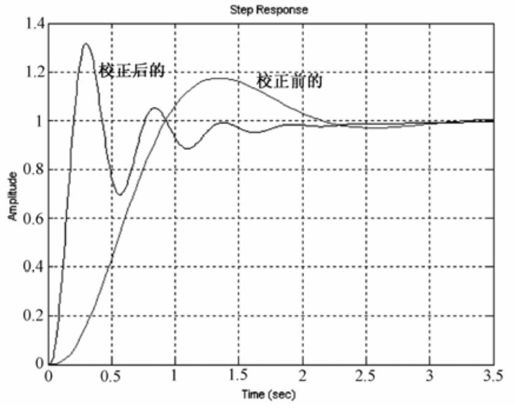
P_225-1

图8.33　例8-8系统校正前后单位阶跃响应曲线

系统校正前后的单位脉冲响应曲线如图8.34所示。

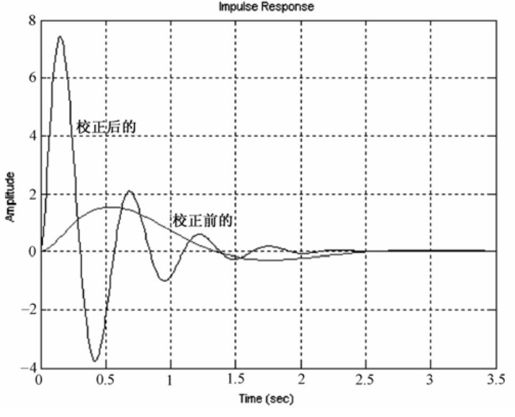
P_225-2

图8.34　例8-8系统校正前后单位脉冲响应曲线

系统校正前后的根轨迹曲线如图8.35所示。

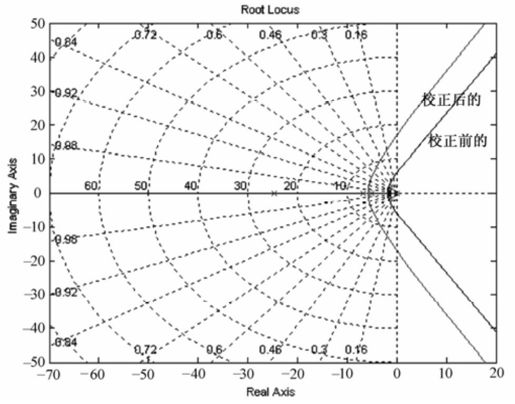
P_225-3

图8.35　例8-8系统校正前后根轨迹图

由运行结果可知，串联超前校正环节的传递函数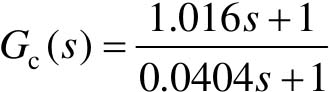H_0014。在阶跃响应图上单击鼠标右键，选择弹出菜单“Charateristics”，分别选择“Peak Response”、“Rise Time”、“Setting Time”便可得到系统的超调、上升时间和调节时间。由运行图可知，校正前的系统超调为σ=17.3%，上升时间tr=0.58 s，调节时间ts=2.92 s；校正后的系统超调为σ=31.7%，上升时间tr=0.123 s，调节时间ts=2.3 s，可知校正后系统的性能提高了。

从根轨迹图可以看出，校正后系统根轨迹左移，从而提高系统的相对稳定性，缩短系统调节时间。

【例8-9】　已知系统开环传递函数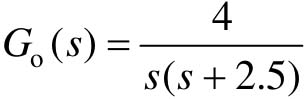H_0015，试设计滞后校正环节，使其校正后系统的静态速度误差系数Kv≤6，闭环主导极点满足阻尼比ζ=0.407，并绘制校正前后系统的单位阶跃响应曲线、单位脉冲响应曲线和根轨迹。

解：计算串联滞后校正环节参数的子函数MATLAB程序代码如下。

  1. %采用根轨迹法设计的串联滞后校正的子函数
  2. %G为校正前系统的开环传递函数；Gc为校正环节的传递函数
  3. function [Gc, kc]=zhjz_root(G, zeta, wc, Tz)
  4. G=tf(G);  [r, k]=rlocus(G)
  5. za=zeta/sqrt(1-zeta^2)
  6. ri=r(1, find(imag(r(1, :))>0))
  7. ra=imag(ri)./real(ri)
  8. kc=spline(ra, k(find(imag(r(1, :))>0)), 1/za)
  9. syms x; syms ng; syms dg
  10. ng=poly2sym(G.num{1}) ; dg=poly2sym(G.den{1})
  11. ess=limit(ng*kc/dg*x)
  12. beta=round(100/sym2poly(ess)/wc);  Tp=Tz/beta
  13. Gc=tf([1, Tz], [1, Tp])

主函数的代码如下：

  1. num=4; den=conv([1, 0], [1, 2.5] ); G=tf(num, den)  %建立校正前系统的传递函数
  2. zeta=0.407; wc=6; Tz=0.1
  3. [Gc, Kc]=zhjz_root(G, zeta, wc, Tz)
  4. GGc=G*Gc*Kc           %校正后系统的开环传递函数
  5. Gy_close=feedback(G, 1)         %校正前系统的闭环传递函数
  6. Gx_close=feedback(GGc, 1)         %校正后系统的闭环传递函数
  7. figure(1);  step(Gx_close, 'b');  hold on     %绘制校正后系统的单位阶跃响应图
  8. step(Gy_close, 'r');  grid        %绘制校正前系统的单位阶跃响应图
  9. gtext('校正前的');  gtext('校正后的')      %放置曲线的文字注释
  10. figure(2);  impulse(Gx_close, 'b');  hold on     %绘制校正后系统的单位冲激响应图
  11. impulse(Gy_close, 'r');  grid        %绘制校正前系统的单位冲激响应图
  12. gtext('校正前的');  gtext('校正后的')      %放置曲线的文字注释
  13. figure(3);  rlocus(G, GGc);  grid       %绘制校正后系统的根轨迹图
  14. gtext('校正前的');  gtext('校正后的')      %放置曲线的文字注释

运行结果如下：

  1. %滞后校正环节传递函数
  2. s + 0.1
  3. ---------
  4. s + 0.025
  5. %系统增益
  6. Kc =    2.3581
  7. %校正后系统闭环传递函数
  8.          9.433 s + 0.9433
  9. ----------------------------------
  10. s^3 + 2.525 s^2 + 9.495 s + 0.9433

系统校正前后的单位阶跃响应曲线如图8.36所示。

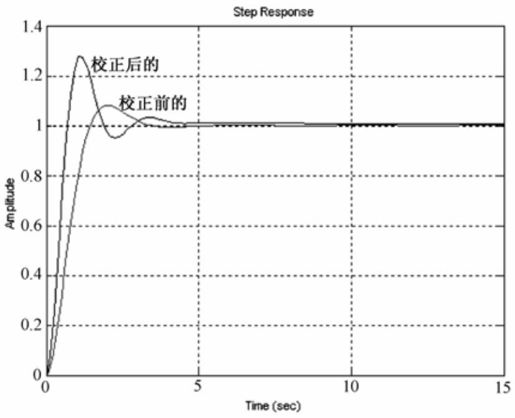
P_227-1

图8.36　例8-9系统校正前后单位阶跃响应曲线

系统校正前后的单位脉冲响应曲线如图8.37所示。

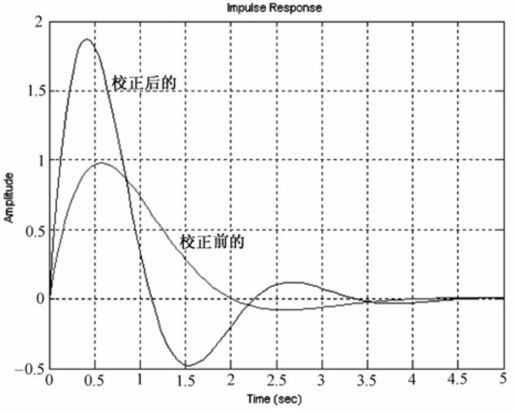
P_227-2

图8.37　例8-9系统校正前后单位脉冲响应曲线

系统校正前后的根轨迹曲线如图8.38所示。

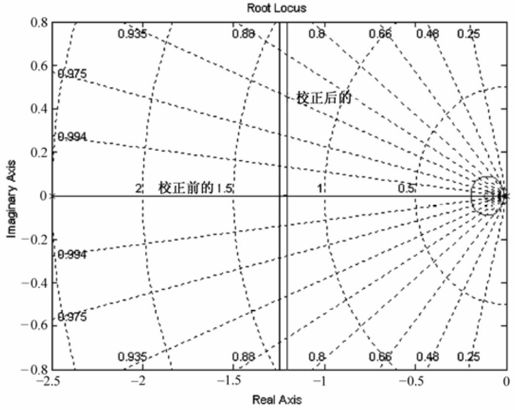
P_228-1

图8.38　例8-9系统校正前后根轨迹

由运行结果可知，串联超前校正环节的传递函数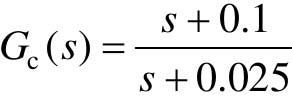H_0016。在阶跃响应图上单击鼠标右键，选择弹出菜单“Charateristics”，分别选择“Peak Response”、“Rise Time”、“Setting Time”，便可得到系统的超调、上升时间和调节时间。由运行图可知，校正前的系统超调为σ=8.08%，上升时间tr=0.961s，调节时间ts=2.99 s；校正后的系统超调为σ=27.4%，上升时间tr=0.478 s，调节时间ts=2.3 s，可知校正后系统的性能提高了。

【例8-10】　已知系统开环传递函数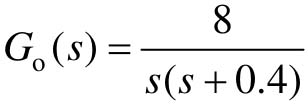H_0017

试设计超前滞后校正环节，使其校正后系统的静态速度误差系数Kv≤5，闭环主导极点满足阻尼比ζ=0.2和自然振荡角频率ωn=5 rad/s，相角裕度为50°，并绘制校正前后系统的单位阶跃响应曲线、单位脉冲响应曲线和根轨迹。

解：函数MATLAB程序代码如下。

  1. z=[];  p=[0, -0.4];  k=8
  2. Gz=zpk(z, p, k);  G=tf(Gz)
  3. zeta=0.2; wn=5
  4. kc=1;  Tz=0.1;  dPm=50+5
  5. ng=G.num{1}; dg=G.den{1}
  6. [num, den]=ord2(wn, zeta)
  7. s=roots(den)
  8. s1=s(1)
  9. Gc1=cqjz_root(G, s1, kc)
  10. G1=G*Gc1*kc
  11. [Gc2, Kc2]=zhjz_root(G, zeta, wn, Tz)
  12. GGc=G1*Gc2*Kc2           %校正后系统的开环传递函数
  13. Gy_close=feedback(G, 1)        %校正前系统的闭环传递函数
  14. Gx_close=feedback(GGc, 1)       %校正后系统的闭环传递函数
  15. figure(1);  step(Gx_close, 'b');  hold on    %绘制校正后系统的单位阶跃响应图
  16. step(Gy_close, 'r');  grid       %绘制校正前系统的单位阶跃响应图
  17. gtext('校正前的'); gtext('校正后的')    %放置曲线的文字注释
  18. figure(2);  impulse(Gx_close, 'b');  hold on  %绘制校正后系统的单位冲激响应图
  19. impulse(Gy_close, 'r');  grid     %绘制校正前系统的单位冲激响应图
  20. gtext('校正前的'); gtext('校正后的')    %放置曲线的文字注释
  21. figure(3);  rlocus(G, GGc);  grid      %绘制校正后系统的根轨迹图
  22. gtext('校正前的'); gtext('校正后的')    %放置曲线的文字注释

运行结果如下：

  1. %超前校正环节传递函数
  2. 1.358 s + 1
  3. -----------
  4. 0.425 s + 1
  5. %滞后校正环节传递函数
  6. s + 0.1
  7. ----------
  8. s + 0.0125
  9. %校正后系统闭环传递函数
  10.      1.358 s^2 + 1.136 s + 0.1
  11. ------------------------------------------------
  12. 0.425 s^4 + 1.175 s^3 + 1.773 s^2 + 1.141 s + 0.

系统校正前后的单位阶跃响应曲线如图8.39所示。

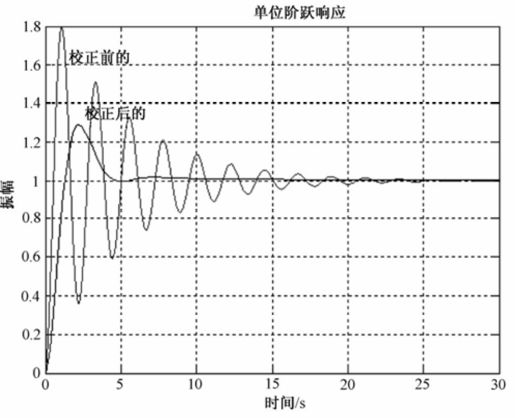
P_229-1

图8.39　例8-10系统校正前后单位阶跃响应曲线

系统校正前后的单位脉冲响应曲线如图8.40所示。

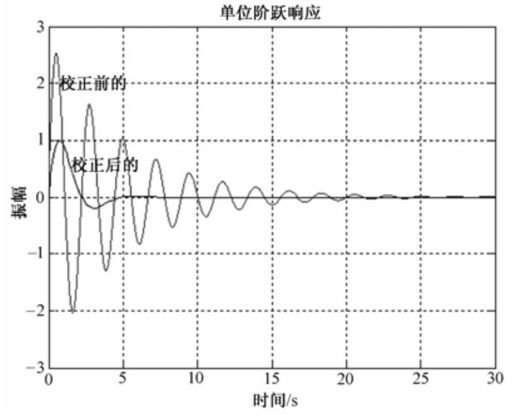
P_230-1

图8.40　例8-10系统校正前后单位脉冲响应曲线

系统校正前后的根轨迹如图8.41所示。

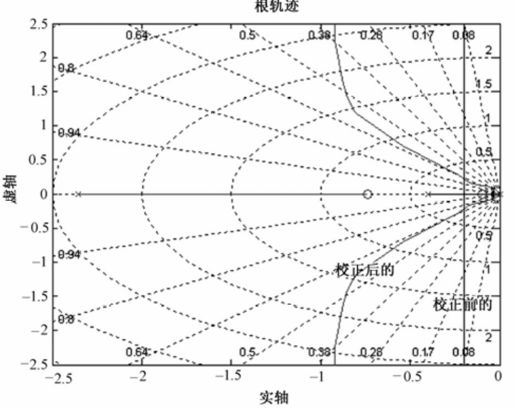
P_230-2

图8.41　例8-10系统校正前后根轨迹

由运行结果可知，串联超前校正环节的传递函数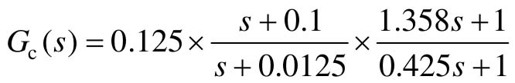H_0018。在阶跃响应图上单击鼠标右键，选择弹出菜单“Charateristics”，分别选择“Peak Response”、“Rise Time”和“Setting Time”，便可得到系统的超调、上升时间和调节时间。由运行图可知，校正前的系统超调为σ=79.9%，上升时间tr=0.384 s，调节时间ts=19.1s；校正后的系统超调为σ=28.9%，上升时间tr=0.907 s，调节时间ts=4.19 s，可知校正后，系统的性能显著提高了。