我的书签
添加书签
移除书签7.5 频率响应分析
时域分析法是分析控制系统的直接方法，时域分析中的性能指标直观地反映了控制系统的动态响应特征；频域分析法是一种工程上广为采用的、间接的系统分析与综合方法，系统频率特性函数的某些特征可用做间接反映系统动态响应的特征。
7.5.1 开环频率特性的性能分析
7.5.1.1 开环对数频率特性与时域响应的关系
根据系统开环对数频率特性对系统性能的不同影响，将系统开环对数频率特性分为3个频段加以分析，即低频段、中频段和高频段。
- 低频段
低频段通常指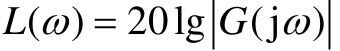
的渐近线在第一个转折频率之前的频段，这一频段的特性完全由积分环节和开环放大倍数决定。
低频段对数幅频特性为：
式中，K为开环放大倍数，v为开环传递函数中积分环节的个数。
若已知低频段的开环对数幅频特性曲线，则很容易得到K值和积分环节数v，故低频段的频率特性决定了系统的稳态性能。
低频段的斜率越小，位置越高，对应系统积分环节的数目越多（系统型号越高），开环放大倍数K越大，则在闭环系统稳定的条件下，其稳态误差越小，动态响应的跟踪精度越高。
- 中频段
中频段指开环对数幅频特性曲线在开环截止频率ωc附近（0 dB附近）的区段，这一频段的特性集中反映了闭环系统动态响应的平稳性和快速性。
时域响应的动态特性主要取决于中频段的形状。
反映中频段形状的三个参数为：开环截止频率ωc、中频段斜率、中频段宽度。ωc的选择，决定于系统暂态、响应速度的要求；中频段越长，相位裕量越大。
开环对数幅频特性中频段斜率最好为-20 dB/dec，而且希望其长度尽可能长些，以确保系统有足够的相角裕量。当中频段的斜率为-40 dB/dec时，中频段占据的频率范围不宜过长，否则相裕量会很小；若中频段斜率更小（如-60 dB/dec），系统就难以稳定。另外，截止频率ωc越高，系统复现信号能力越强，系统快速性也就越好。
- 高频段
高频段指开环对数幅频特性在中频段以后的频段，高频段的形状主要影响时域响应的起始段。
在进行分析时，可以将高频段进行近似处理，即用一个小惯性环节来等效地替代多个小惯性环节，等效的小惯性环节的时间常数等于被替代的多个小惯性环节的时间常数之和。
系统开环对数幅频特性在高频段的幅值，直接反映了系统对高频干扰信号的抑制能力。高频部分的幅值越低，系统的抗干扰能力越强。
总之，为了使系统满足一定的稳态和动态要求，对开环对数幅频特性的形状有如下要求：低频段要有一定的高度和斜率；中频段的斜率最好为-20 dB/dec，且具有足够的宽度；高频段采用迅速衰减的特性，以抑制不必要的高频干扰。
需要注意的是，3个频段的划分并没有严格的确定准则，但是3个频段的概念为直接运用开环频率特性来判别、估算系统性能指出了方向。
7.5.1.2 开环频率特性与时域响应的关系
由开环频率特性来研究系统的时域响应暂态性能，通常有两个：
（1）相角裕量γ，它反映系统的相对稳定性；它是在频域内描述系统稳定程度的指标，而系统的稳定程度直接影响时域指标超调量σ%和调节时间ts，γ与σ%和ts存在内在联系。
（2）截止频率ωc，它反映系统的快速性。ωc是A(ωc)=1所对应的角频率，或对数幅频特性图上L(ω)穿越0分贝线的斜率。
对于典型的二阶系统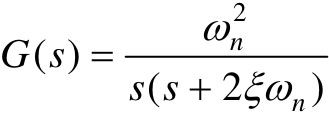
，其结构参量ξ、ωn，在时域分析中已建立了与时域指标间的关系式，即，
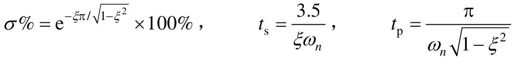
根据A(ωc)=1可以求得ωc、γ与ξ之间的关系如下：
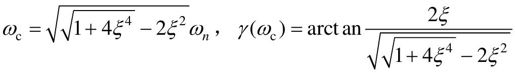
从上面可以看出，时域和频域的指标都可用ωn和ξ来表示，因此，通过时域指标可以推算出频域指标，反之亦然。
根据上式可以绘制γ(ωc)-ξ曲线，从绘制的曲线上可以看出，γ越大，ξ也越大；γ越小，ξ就越小。要想得到满意的动态过程，一般γ取值范围为30°～70°。
由开环对数幅频特性求时域指标的方法：首先从开环对数幅频特性曲线上求得ωn和γ值，然后根据γ值查γ(ωc)-ξ曲线获得ξ值，最后由ξ值可得到σ%；根据ωn、ξ可求得tp和ts。
对于高阶系统，γ毕竟只是比较简单的一项指标，它不能完全概括千变万化的频率特性形状。γ相同的系统，频率特性未必完全相同，因此时域指标也不会一样。因此在高阶系统中，γ与时域指标之间没有确定的函数关系。通过对大量系统的研究可归纳出下面两个近似的计算公式：
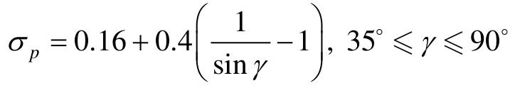
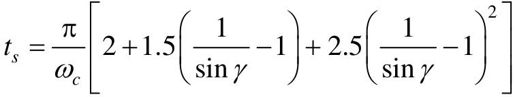
需要指出的是，根据上述公式计算所得结果，当γ较小时，比较接近实际系统，即准确度高；而当γ较大时，近似程度较差，准确度低。
7.5.2 闭环频率特性的性能分析
7.5.2.1 闭环频率特性与时域响应的关系
对于二阶系统，其频域性能指标与时域性能指标之间存在一定的数学关系。
二阶系统的闭环传递函数为：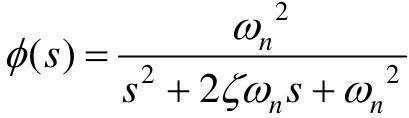
。
系统的闭环频率特性为：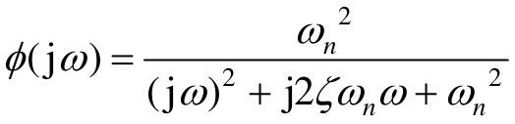
。
系统的闭环幅频特性为：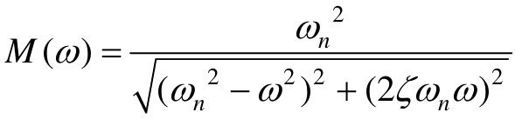
。
系统的闭环相频特性为：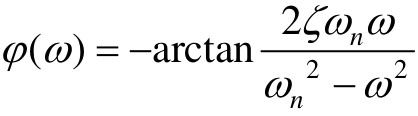
。
二阶系统的谐振峰值Mr与时域超调量Mp之间的关系为：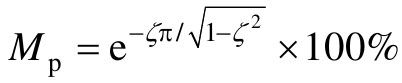
，
。
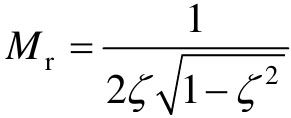从上面的式子可以看出：
（1）谐振峰值Mr仅与阻尼比ζ有关，超调量Mp也仅取决于阻尼比ζ；
（2）ζ越小，Mr增加得越快，此时超调量Mp会很大，超过40%，这样的系统一般不符合瞬态响应指标的要求；
（3）当0.4<ζ<0.707时，Mr与Mp的变化趋势基本一致，此时谐振峰值Mr=1.2～1.5，超调量Mp=20%～30%，系统响应结果比较理想；
（4）当ζ>0.707时，无谐振峰值，Mr与Mp的对应关系不再存在，通常在设计中ζ取值在0.4至0.7之间。
二阶系统的谐振频率ωr与峰值时间tp之间的关系为：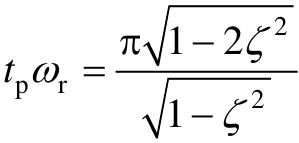
。
从上式可以看出，当ζ为常数时，谐振频率ωr与峰值时间pt成反比，ωr值越大，tp越小，表示系统时间响应越快。
二阶系统的闭环截止频率ωb与过渡过程时间ts之间的关系为：
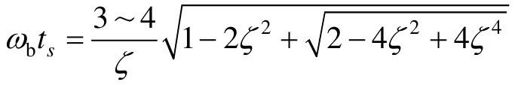
从上式可以看出，当阻尼比ζ给定后，闭环截止频率ωb与过渡过程时间ts成反比。换言之，ωb越大（频带宽度越宽），系统的响应速度越快。
7.5.2.2 闭环系统的等M圆和等N圆
为了便于用闭环频率特性的指标Mp、ωp来分析和设计系统，通常采用直角坐标系的等M圆和对数坐标的等N图。
- 等M圆
设开环频率特性G(jω)为：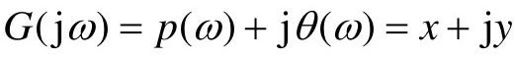
。
则闭环频率特性的幅值为：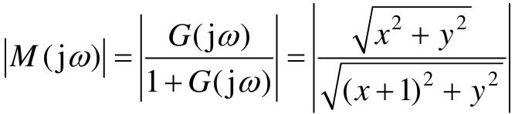
。
令M=|M(jω)|，则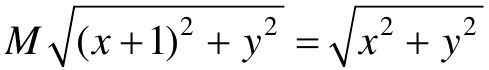
，整理得：
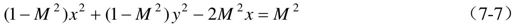
当M=1时，由上式可求得x=-1/2，这是通过点（-1/2, j0）且与虚轴平行的一条直线；
当M≠1时，式（7-7）可化简为：
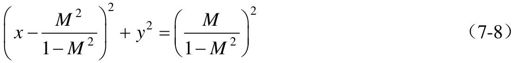
当给定M值（等M值）时，上式是一个圆方程式，圆心在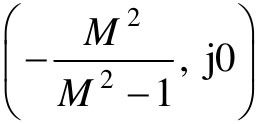
处，半径为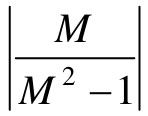
因此在G(jω)平面上，等M圆轨迹是一簇圆，如图7.5所示。
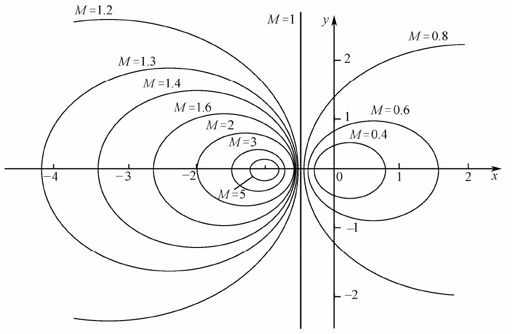
图7.5 等M圆轨迹
从图7.5中可以看出：
- 当M>1时，随着M值的增大，等M圆半径越来越小，最后收敛于（-1, j0）点，且这些圆均在M=1直线的左侧。
- 当M<1时，随着M值的减小，等M圆半径也越来越小，最后收敛于原点，且这些圆都在M=1直线的右侧。
- 当M=1时，它是通过（-1/2, j0）点平行于虚轴的一条直线。等M圆既对称于M=1的直线，又对称于实轴。
如果将开环频率特性的极坐标图G(jω)叠加在等M圆线上，如图7.6所示，则由幅相特性与等M圆的切点可以确定系统的谐振频率ωr和谐振峰值Mr。
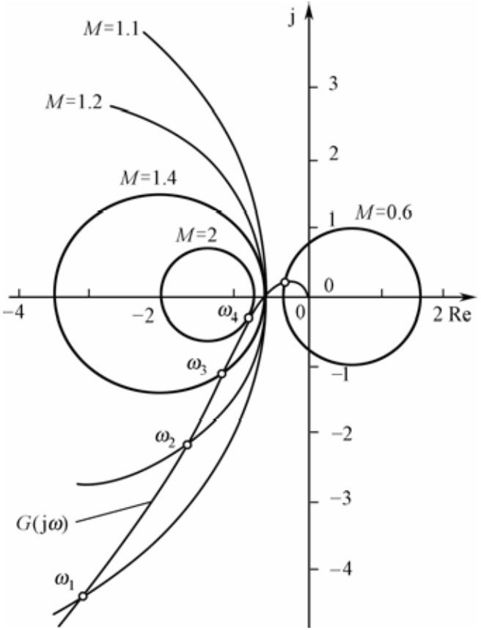
图7.6 等M圆和系统开环幅相频率特性
从图7.6可以分析出，G(jω)曲线与等M圆相交于ω1,ω2,ω3,…。在ω=ω1处，G(jω)曲线与M=1.1的等M圆相交，表明在ω1频率下，闭环系统的幅值为M(ω1)=1.1，以此类推。
从图7.6中还可看出，M=2的等M圆正好与G(jω)曲线相切，切点处的M值最大，即为闭环系统的谐振峰值Mr，而切点处的频率即为谐振频率ωr。
此外，G(jω)曲线与M=0.707的等M圆交点处的频率为闭环系统的截止频率ωb，0<ω<ωb称为闭环系统的频带宽度。
- 等N圆
闭环频率特性的相角φm为：
。
令N=tanφm，整理得：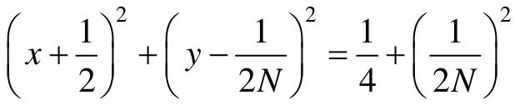
。
当给定N值（等N值）时，上式是一个圆方程式，圆心在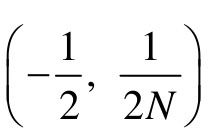
处，半径为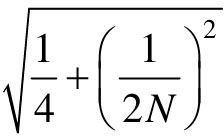
，称为等N圆，如图7.7所示。
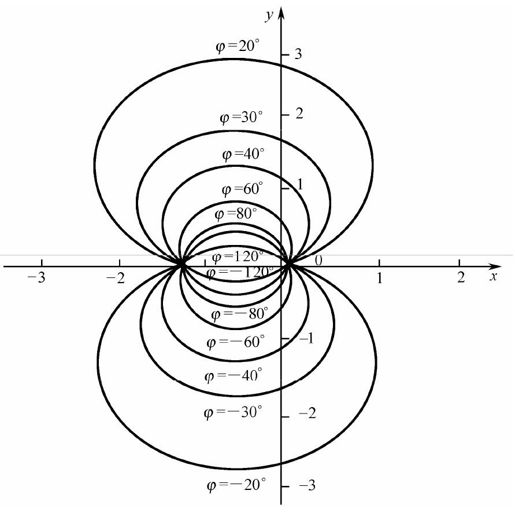
图7.7 等N圆
等N圆实际上是等相角正切的圆，当相角增加±180°时，其正切相同，因而在同一个圆上。
所有等N圆均通过原点和（-1, j0）点，对于等N圆，并不是一个完整的圆，而只是一段圆弧。
如果将开环频率特性的极坐标图G(jω)叠加在等N圆线上，如图7.8所示，则可以利用开环频率特性求出闭环系统的相角和角频率ω之间的关系。
幅相特性与等M圆的切点可以确定系统的谐振频率ωr和谐振峰值Mr。
从图7.8可以分析出，G(jω)曲线与等N圆相交于ω1,ω2,ω3,…。在ω=ω1处，G(jω)曲线与-10°的等N圆相交，表明在ω1频率下，闭环系统的相角为-10°，以此类推可得闭环相频特性。
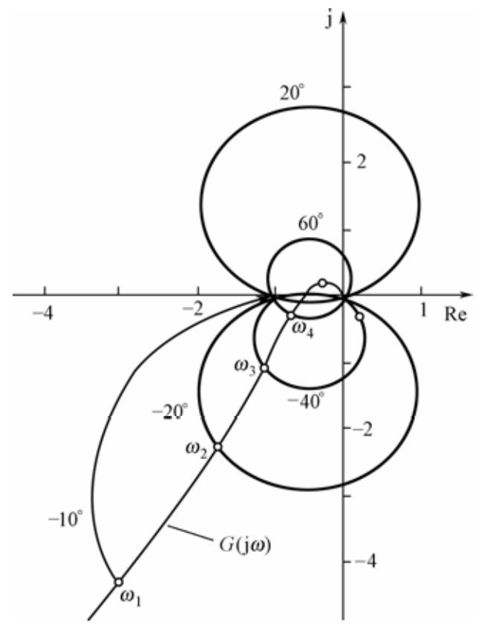
图7.8 等N圆和系统开环幅相频率特性
