2.4　MATLAB数值计算

MATLAB是一门计算语言，它的运算指令和语法基于一系列基本的矩阵运算以及它们的扩展运算，它支持的数值元素是复数，这也是MATLAB区别于其他高级语言的最大特点之一，它给许多领域的计算带来了极大方便。因此，为了更好地利用MATLAB语言的优越性和简捷性，首先需要对MATLAB的数值类型、数组矩阵的基本运算、符号运算、关系运算和逻辑运算进行介绍，并给出应用实例，本部分的内容是后面章节的基础。

2.4.1　MATLAB数值类型

MATLAB包括4种基本数据类型，即双精度数组、字符串数组、元胞数组、构架数组。数值之间可以相互转化，这为其计算功能开拓了广阔的空间。

2.4.1.1　变量与常量

变量是数值计算的基本单元。与C语言等其他高级语言不同，MATLAB语言中的变量无须事先定义，一个变量以其名称在语句命令中第一次合法出现而定义，运算表达式变量中不允许有未定义的变量，也不需要预先定义变量的类型，MATLAB会自动生成变量，并根据变量的操作确定其类型。

  1. MATLAB变量命名规则

MATLAB中的变量命名规则如下：

（1）变量名区分大小写，因此A与a表示的是不同的变量；

（2）变量名以英文字母开始，第一个字母后可以使用字母、数字、下画线，但不能使用空格和标点符号；

（3）变量名长度不得超过31位，超过的部分将被忽略；

（4）某些常量也可以作为变量使用，如i在MATLAB中表示虚数单位，但也可以作为变量使用。

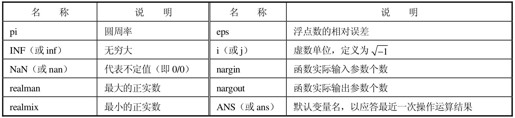
常量是指那些在MATLAB中已预先定义其数值的变量，默认的常量如表2.3所示。

表2.3　MATLAB默认常量

034-2

  1. MATLAB变量的显示

任何MATLAB语句的执行结果都可以在屏幕上显示，同时赋值给指定的变量，没有指定变量时，赋值给一个特殊的变量ans，数据的显示格式由format命令控制。format只影响结果的显示，不影响其计算与存储。MATLAB总是以双字长浮点数（双精度）来执行所有的运算。如果结果为整数，则显示没有小数；如果结果不是整数，则输出形式如表2.4所示的几种形式。

表2.4　MATLAB的数据显示格式

035-1

  1. MATLAB变量的存取

工作空间中的变量可以用save命令存储到磁盘文件中。输入命令“save<文件名>”，将工作空间中全部变量存到“<文件名>.mat”文件中去，若省略“<文件名>”则存入文件“matlab.mat”中；命令“save<文件名><变量名集>”将“<变量名集>”指出的变量存入文件“<文件名>.mat”中。

用命令load可将变量从磁盘文件读入MATLAB的工作空间，其用法为“load<文件名>”，它将“<文件名>”指出的磁盘文件中的数据依次读入名称与“<文件名>”相同的工作空间中的变量中去。若省略“<文件名>”则“matlab.mat”从中读入所有数据。

用clear命令可从工作空间中清除现存的变量。

变量的存取可参考2.2.4节，有更详细的介绍。

2.4.1.2　字符串

字符是MATLAB中符号运算的基本元素，也是文字等表达方式的基本元素，在MATLAB中，字符串作为字符数组用单引号（’）引用到程序中，还可以通过字符串运算组成复杂的字符串。字符串数值和数字数值之间可以进行转换，也可以执行字符串的有关操作。

2.4.1.3　元胞数组

元胞是元胞数组（Cell Array）的基本组成部分。元胞数组与数字数组相似，以下标来区分，单元胞数组由元胞和元胞内容两部分组成。用花括号{ }表示元胞数组的内容，用圆括号( )表示元胞元素。与一般的数字数组不同，元胞可以存放任何类型、任何大小的数组，而且同一个元胞数组中各元胞的内容可以不同。

【例2-1】　元胞数组创建与显示举例。

解：MATLAB程序代码如下。

  1. A(1, 1)={'An example of cell array'}; 
  2. A(1, 2)={[1 2;3 4]}; A{2, 1}=tf (1, [1, 8]); A{2, 2}={A(1, 2);’This is an example’}; 
  3. celldisp(A)  %显示该元胞数组

元胞数组A第1行用元胞数组标志法建立一个字符串和一个矩阵；第2行用元胞内容编址法，建立一个传递函数和一个由两个元素组成的元胞组，该元胞组分别是矩阵和字符串，最后，用celldisp函数显示该元胞数组A。

2.4.1.4　构架数组

与元胞数组相似，构架数组（Structure Array）也能存放各类数据，使用指针方式传递数值。构架数组由结构变量名和属性名组成，用指针操作符“.”连接结构变量名和属性名。例如，可用parameter.temperature表示某一对象的温度参数，用parameter.humidity表示某一对象的湿度参数等，因此，该构架数组parameter由两个属性组成。

2.4.1.5　对象

面向对象的MATLAB语言采用了多种对象，如自动控制中常用的传递函数模型对象（tf object）、状态空间模型对象（ss object）和零极点模型对象（zpk object），一些对象之间可以相互转换，例如可以从传递函数模型对象转化为零极点模型对象，这将在后面具体介绍。

2.4.2　矩阵运算

MATLAB软件的最大特色是强大的矩阵计算功能，在MATLAB软件中，所有的计算都是以矩阵为单元进行的，可见矩阵是MATLAB的核心。下面以表格的形式列出MATLAB提供的每类矩阵运算的函数，并各举一个实例进行说明，同类函数的用法基本类似，详细的用法及函数内容说明可参考联机帮助。

2.3.2.1　矩阵基本概念

由m行n列构成的数组a称为m×n阶矩阵，它总共由m×n个元素组成，矩阵元素记为aij，其中i表示行，j表示列。

当m=n时，矩阵a称为方阵。当i≠j时，所有的aji=0，且m=n，得到的矩阵称为对角阵。

当对角阵的对角线上的元素全为1时，称为单位阵，记为I。

对于m×n阶矩阵w，当wij=aji时，称w是a的转置矩阵，记为w=a′。

对于a为m×1的形式时，称a是m个元素的列向量，对于a为1×n的形式时，称a是n个元素的行向量。

2.3.2.2　矩阵建立与访问

矩阵的表现形式和数组相似，它以左方括号“[”开始，以右方括号“]”结束，每一行元素结束用行结束符号（分号“;”）或回车符分割，每个元素之间用元素分割符号（空格或“，”）分隔。建立矩阵的方法有直接输入矩阵元素、在现有矩阵中添加或删除元素、读取数据文件、采用现有矩阵组合、矩阵转向、矩阵移位及直接建立特殊矩阵等。

【例2-2】　创建矩阵举例。

解：MATLAB程序代码如下。

  1. >> a=[1 2 3;4 5 6]

运行结果是创建了一个2×3的矩阵a，a的第1行由1、2、3这3个元素组成，第2行由4、5、6这3个元素组成，输出结果如下：

  1. a = 1     2     3
  2.      4     5     6

接着输入：

  1. >> b=[a;11,12,13]  %添加一行元素[11,12,13]

运行结果是创建了一个3×3的矩阵b，b矩阵是在a矩阵的基础上添加一行元素11、12、13，组成一个3×3矩阵，输出结果如下：

  1. b = 1     2     3
  2.    4     5     6
  3.    11    12    1

MATLAB中对矩阵元素的访问如下所示：

  • 单个元素的访问：b(3, 2)→12，访问了第3行和第2列交叉的元素；
  • 整列元素的访问：b(:, 3)→[3, 6, 13]’，访问了第3列中的所有元素；
  • 整行元素的访问：b(1,:)→[1, 4, 11]，访问了第1行中的所有元素；
  • 整块元素的访问：b(2:3, 2:3)→[5, 6; 12, 13]，访问了一个（2×2）的子块矩阵。

2.4.2.3　特殊矩阵生成

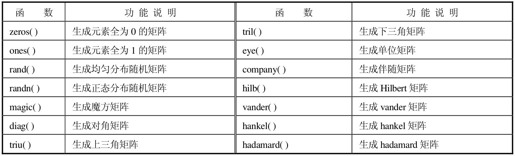
MATLAB提供了很多个特殊矩阵的生成函数，表2.5列出了一些常用的生成函数，关于其他的特殊矩阵生成函数及使用格式，请参见联机帮助。

表2.5　MATLAB常用特殊矩阵生成函数

037

【例2-3】　特殊矩阵生成函数举例。

解：MATLAB程序代码如下。

  1. >> a=[1, 2, 3; 4, 5, 6; 7, 8, 9];  b=tril(a)  %生成下三角矩阵

运行结果是生成了b矩阵，它是调用下三角矩阵生成函数tril( )生成的a矩阵的下三角矩阵，输出结果如下：

  1. b = 1     0     0
  2.    4     5     0
  3.    7     8     9

2.4.2.4　矩阵基本运算

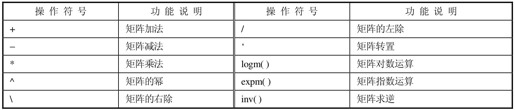
矩阵与矩阵之间可以进行如表2.6所示的基本运算。

注意

在进行左除“/”和右除“\”时，两矩阵的维数必须相等。

表2.6　矩阵基本运算

038-1

【例2-4】　矩阵基本运算举例。

解：MATLAB程序代码如下。

  1. >> a=[1,2;3,4];  b=[3,5;2,9];  div1=a/b;    %矩阵的左除
  2. >>div2=b\a   %矩阵的右除

两矩阵a，b进行了左除和右除运算，输出结果如下：

  1. div1 =                          div2 =
  2.   0.2941    0.0588                -0.3529   -0.1176
  3.    1.1176   -0.1765                0.4118    0.4706

2.4.2.5　矩阵函数运算

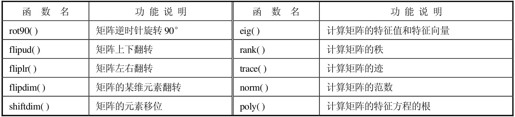
MATLAB提供了多种关于矩阵的函数，表2.7列出了一些常用的矩阵函数运算。

表2.7　常用矩阵函数运算

038-2

【例2-5】　矩阵函数运算举例。

解：MATLAB程序代码如下。

  1. >> a=[1, 3, 5; 2, 4, 6; 7, 9, 13];  [b, c]=eig(a)   %求取矩阵的特征值和特征向量

通过函数eig( )计算矩阵a的特征向量b和特征值c，输出结果如下：

  1. b =-0.3008   -0.7225    0.2284
  2.    -0.3813   -0.3736   -0.8517
  3.    -0.8742    0.5817    0.4717
  4. c =   19.3341         0         0
  5.          0   -1.4744         0
  6.          0         0    0.1403

2.4.2.6　矩阵分解运算

矩阵分解常用于方程求根，表2.8列出了一些常用的矩阵分解运算。

表2.8　常用矩阵分解运算函数

039-1

【例2-6】　矩阵分解运算函数举例。

解：MATLAB程序代码如下。

  1. >> a=[6, 2, 1; 2, 3, 1; 1, 1, 1];  [L, U, P]=lu(a)  %对矩阵进行LU分解

通过函数lu( )对矩阵a进行LU分解，得到上三角阵U、下三角阵L、置换矩阵P，输出结果如下：

  1. L = 1.0000     0           0                U =  6.0000    2.0000    1.0000
  2.      0.3333     1.0000     0                      0          2.3333    0.6667
  3.      0.1667     0.2857     1.0000                0          0          0.6429
  4. P = 1     0    0
  5.      0     1    0
  6.      0     0    1