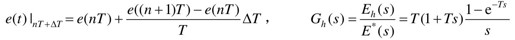12.2　离散控制系统基本概念

12.2.1　离散控制系统概述

数字、离散控制系统与连续控制系统的根本区别在于：

（1）离散控制系统中既可以包含连续信号，又可以包含离散信号，是一个混合信号系统。

（2）连续系统中的控制信号、反馈信号以及偏差信号都是连续型的时间函数，而在离散系统中则不然。一般情况下，其控制信号是离散型的时间函数，因此取自系统输出端的负反馈信号在和离散控制信号进行比较时，同样需要采用离散型的时间函数，那么比较后得到的偏差信号也将是离散型的时间函数。

（3）分析和设计数字、离散控制系统的数学工具是Z变换，采用的数学模型是差分方程、脉冲传递函数。

12.2.1.1　离散控制系统基本组成

离散控制系统结构形式多样，一般如图12.1所示，主要由采样器、数字控制器、保持器、执行器、被控对象和测量变送器构成。

图12.1　离散控制系统结构示意图

（1）采样器：将连续信号转换成脉冲序列。

（2）数字控制器：常用的是数字计算机，构成控制系统的数字部分，对系统进行控制，通过这部分的信号均以离散形式出现。

（3）保持器：将数字控制器输出的离散信号转换成模拟信号，用来实现采样点之间的插值，常见的保持器有零阶保持器和一阶保持器。

（4）执行器：根据控制器的控制信号，改变输出的角位移或直线位移，并通过调节机构改变被调介质的流量或能量，使工作过程符合预定要求。按照不同的动力方式可分为电动执行器、气动执行器和液动执行器。

（5）被控对象：所要控制的装置或设备。

（6）测量变送器：通常由传感器和测量线路构成，用于将被控参数转换成某种形式的信号。

12.2.1.2　数字控制系统工作过程

数字控制系统通过数字计算机闭合而成，包括工作于离散状态下的数字计算机（或专用数字控制器）和具有连续工作状态的被控对象两大部分，其工作过程如图12.2所示。图中虚线内为用于控制目的的数字计算机或数字控制器，它构成控制系统的数字部分，通过这部分的信号均以离散形式出现；被控对象一般用G(s)表示，是系统的不可变部分，它是控制系统连续部分的主要成分。

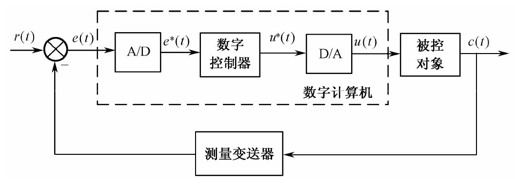
图12.2　数字控制系统工作示意图

在数字控制系统中，具有连续时间函数形式的被控信号c(t)（模拟量）受控于具有离散时间函数形式的控制信号u(t)（数字量）。为了实现控制，需要通过数/模转换环节（D/A）将数字量转换为模拟量，即将u(t)转换为u(t)。连续的被控信号c(t)经反馈环节反馈至输入端并与参考输入r(t)进行比较，得到e(t)，e(t)经模/数转换环节（A/D）得到偏差信号e(t)（数字量）。离散的偏差信号e(t)经数字计算机加工处理变换成数字信号u(t)，u(t)再经D/A转换为连续信号u(t)，u(t)馈送到连续部分的执行机构去控制系统的被控信号c(t)。

12.2.1.3　离散控制系统基本特点

离散控制系统在自动控制领域中越来越多地被广泛应用，它具有以下基本特点：

（1）以数字计算机为核心组成数字式控制器，可实现复杂的控制要求，控制效果好，并可通过软件方式改变控制规律，控制方式灵活；

（2）数字信号传输可有效抑制噪声，提高系统的抗干扰能力；

（3）可采用高灵敏度的控制元件，提高系统的控制精度；

（4）可用一台数字计算机实现对几个系统的分时控制，提高设备利用率，经济性好；

（5）对于大滞后、大惯性系统，具有较好的控制效果；

（6）便于组成功能强大的集散控制系统。

12.2.2　离散信号的数学描述

离散系统的一个显著特点是系统中一处或多处信号是脉冲序列或数字序列，而自然界的信号多是连续信号，为了把连续信号变为脉冲信号，需要对连续信号进行采样，为了把脉冲信号变为连续信号则需要用保持器。

12.2.2.1　采样过程及采样定理

1. 采样过程

采样过程是指采样器按一定的时间间隔对连续信号e(t)进行采样，将其转换为相应的脉冲序列，即采样信号e*(t)的获取过程。实现采样过程的装置称为采样器或采样开关。

采样器可以用一个周期性闭合的开关来表示，其闭合周期为T，每次闭合时间为τ。实际上，由于采样持续时间通常远小于采样周期，即τ<<T，也远小于系统连续部分的时间常数，因此，在分析采样系统时，可近似认为τ→0。在这种假设条件下，当采样开关的输入信号为连续信号e(t)时，其输出信号e(t)是一个脉冲序列，采样瞬时e(t)的幅值等于相应瞬时e(t)的幅值，即e(0), e(T), e(2T),…, e(nT)，采样过程如图12.3所示。

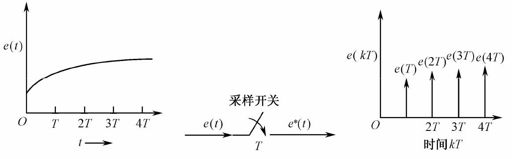
图12.3　采样过程示意图

采样过程可以看成一个脉冲调制过程。理想的采样开关相当于一个单位理想脉冲序列发生器，它能够产生一系列单位脉冲e(0), e(T), e(2T),…, e(nT)。

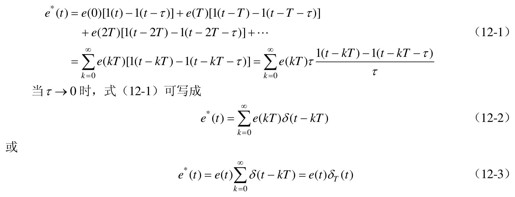
1. 采样定理

采样定理（Shannon定理）是在设计离散系统时必须要遵循的准则，它给出了自采样的离散信号不失真地恢复原连续信号所必需的理论上的最低采样频率。

对于如式（12-3）描述的采样信号e(t)，令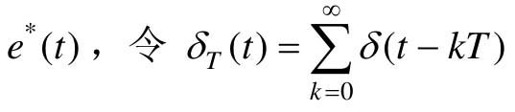，则e(t)可写成

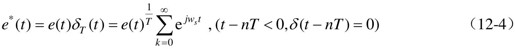
对e*(t)进行拉氏变换，可得

式（12-5）表明，采样函数的拉氏变换式E(s)是以ωs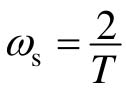（，称为采样角频率）为周期 的周期函数；它还表示了采样函数的拉氏变换式E(s)与连续函数拉氏变换式E(s)之间的关系。

通常E(s)的全部极点均位于S平面的左半部，因此可用jω代替上式中的复变量s，直接求得采样信号的傅里叶变换：

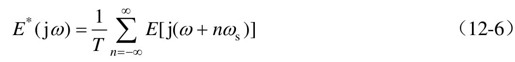
式（12-6）即为采样信号的频谱函数，它也反映了离散信号频谱和连续信号频谱之间的关系。

一般来说，连续函数的频谱是孤立的，其带宽是有限的，即上限频率为有限值，而离散函数e*(t)则具有以ωs为周期的无限多个频谱。

在离散函数的频谱中，n=0的部分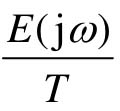称为主频谱，它对应于连续信号的频谱。除了主频谱外，E(jω)还包含无限多个附加的高频频谱。为了准确复现所采样的连续信号，必须使采样后的离散信号的频谱彼此不重叠，这样就可以用一个比较理想的低通滤波器滤掉全部附加的高频频谱分量，保留主频谱。

相邻两频谱互不重叠的条件是

若满足式（12-7）的条件，并把采样后的离散信号e*(t)加到理想滤波器上，则在滤波器的输出端将不失真地复现原连续信号（幅值相差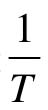倍）。若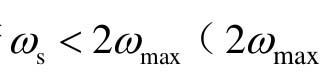为连续信号的有限频率），则会出现相邻频谱的重叠现象，这时即使使用理想滤波器也不能将主频谱分离出来，因而难以准确复现原有的连续信号。

综上可以得到一条重要结论，即只有在ωs≥2ωmax的条件下，采样后的离散信号e*(t)才有可能无失真地恢复为原来的连续信号，这就是香农（Shannon）采样定理。

12.2.2.2　保持器的数学描述

保持器是把数字信号转换成连续信号的装置，从数学上说，它解决了两个采样点之间的插值问题，即根据过去或现在的采样值进行外推，是一种时域的外推装置。

由采样过程的数学描述可知，在采样时刻上，连续信号的函数值与脉冲序列的脉冲强度相等，在nT时刻，有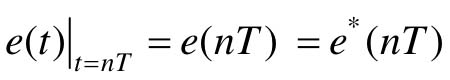，而在(n+1)T时刻，则有。

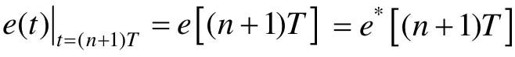然而，由脉冲序列e*(t)向连续信号e(t)的转换过程中，在nT和(n+1)T时刻之间，即当0<Δt<T时，连续信号e(nT+Δt)的值是多少？它与e(nT)有何关系？这就是保持器要解决的)问题。

通常把具有恒值、线性和抛物线外推规律的保持器分别称为零阶、一阶和二阶保持器。其中最简单、最常用的是零阶保持器和一阶保持器，下面分别进行介绍。

1. 零阶保持器

零阶保持器是一种按照恒值规律外推的保持器，它把前一采样时刻nT的采样值e(nT)（在各采样点上e(nT)=e(nT))不增不减地保持到下一采样时刻(n+1)T到来之前，从而使采样信号e(t)变成阶梯信号eh(t)，如图12.4所示。

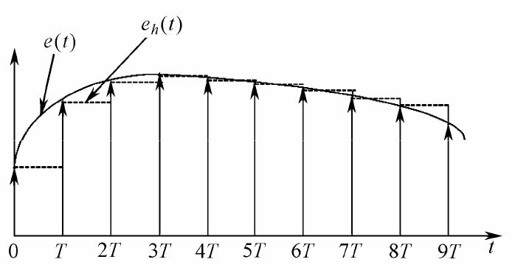
图12.4　零阶保持器输入和输出关系图

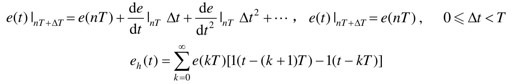
由图12.4可见，零阶保持器的输出信号是阶梯信号，它与要恢复的连续信号是有区别的，包含高次谐波。若将阶梯信号的各中点连接起来，可以得到比连续信号退后T/2的曲线，它这反映了零阶保持器的相位滞后特性。

零阶保持器的传递函数为

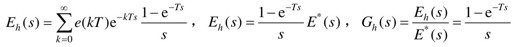
零阶保持器的频率特性为

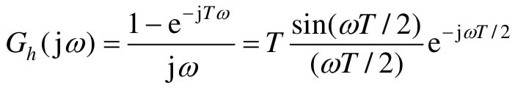
零阶保持器具有如下特性。

（1）低通特性。由于幅频特性的幅值随频率值的增大而迅速衰减，说明零阶保持器基本上是一个低通滤波器，但与理想滤波器特性相比，在ω=ωs/2时，其幅值只有初值的63.7%，且截止频率不止一个，所以零阶保持器除允许主要频谱分量通过外，还允许部分高频分量通过，从而造成数字控制系统的输出中存在纹波。

（2）相角特性。由相频特性可见，零阶保持器要产生相角滞后，且随着频率的增大而加大，在ω=ωs/2时，相角滞后可达-180°，从而使闭环系统的稳定性变差。

（3）时滞特性。零阶保持器的输出为阶梯信号eh(t)，其平均响应为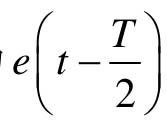，表明输出比输入在时间上要滞后T/2，相当于给系统增加一个延迟时间为T/2的延迟环节，对系统稳定不利。

1. 一阶保持器

一阶保持器是一种按线性规律外推的保持器，其外推关系为

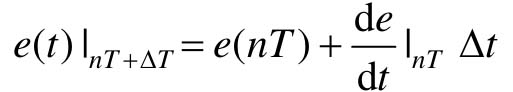
由于未引进高阶差分，一阶保持器的输出信号与原连续信号之间仍有差别。一阶保持器的单位脉冲响应可以分解为阶跃函数和斜坡函数之和。

一阶保持器的单位脉冲函数的拉氏变换式为