6.4　其他形式的根轨迹

前面研究的是以根轨迹放大系数K（回路增益）为变量的根轨迹，本节将讨论几种其他形式的根轨迹，包括正反馈系统的根轨迹、参数根轨迹和时滞系统的根轨迹。

6.4.1　正反馈系统的根轨迹

在正反馈条件下，系统的根轨迹方程改为G(s)H(s)=1。

幅值条件不变，而相角条件则改为：

164-1

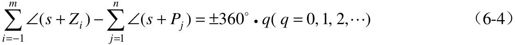
于是与相角有关的三条绘制法则应加以如下修改。

法则3：关于实轴上的根轨迹，原法则中的奇数应改为偶数（包括0）。

法则4：和法则6：关于根轨迹的渐近线与正实轴的夹角和根轨迹的起始角，原法则中的±180°(2q+1)应改为±360°·q。

该方法也可用来绘制负反馈系统中当开环根轨迹增益K<0时的根轨迹。

6.4.2　参数根轨迹

如前所述，一般的根轨迹的绘制总是设定其变化参数是开环增益K，当需要研究系统中任一个其他参数变化对系统动力学性能的影响时，就会涉及到参数根轨迹的问题。

设闭环特征方程为：D(λ,s)=0，其中，λ就是可变参数。可将闭环特征方程改写成：

164-2

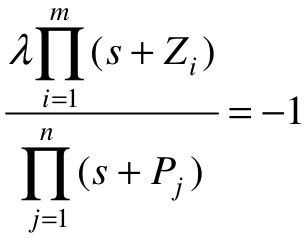
或者

164-3

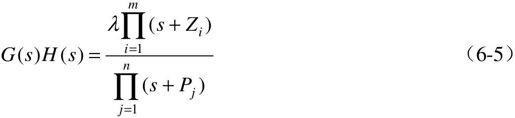
式（6-5）中，G(s)H(s)称为等效开环传递函数，-Zi(i=1,2,…,m)和-Pj(j=1,2,…,n)分别称为等效的开环零点和开环极点。

注意

系统的等效的开环零点和开环极点与实际的开环传递函数和开环零极点是不同的，但由等效根轨迹方程来绘制根轨迹结果就完全一样了。

6.4.3　时滞系统的根轨迹

如果系统开环传递函数中含有滞后时间为τ的时滞环节e-τs，则根轨迹方程可写成：

165-1

由式（6-6）绘制根轨迹是比较麻烦的，使用中常采用一些近似的方法来处理。

对e-τs进行泰勒级数展开，忽略高次项，可得e-τs≈1-τs；对eτs进行泰勒级数展开，忽略高次项，可得：

165-2

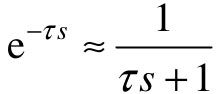
更精确一些的可用所谓的Pade展开式，得到：

165-3

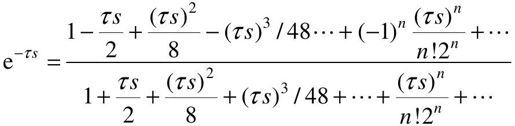
如果取一次近似，则

165-4

6.4.4　利用MATLAB绘制其他形式的根轨迹举例

下面通过几个实例，讲述利用MATLAB绘制其他形式的根轨迹。

【例6-6】　绘制正反馈系统的根轨迹。已知某单位负反馈系统的开环传递函数为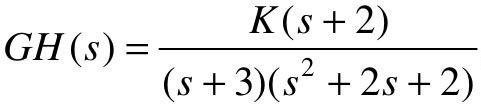165-5，k<0试使用MATLAB画出系统的根轨迹。

解：MATLAB程序代码如下。

  1. num=[1, 2];  den=conv([0, 1, 3], [1, 2, 2]); %传递函数分子、分母多项式系数行向量
  2. sys=tf(num, den)           %建立传递函数模型
  3. rlocus(-sys)               %绘制根轨迹图
  4. axis([-15 5 -10 10])       %调整绘制区域
  5. title('正反馈根轨迹图')     %添加图标题

根轨迹图如图6.13所示。

166-1

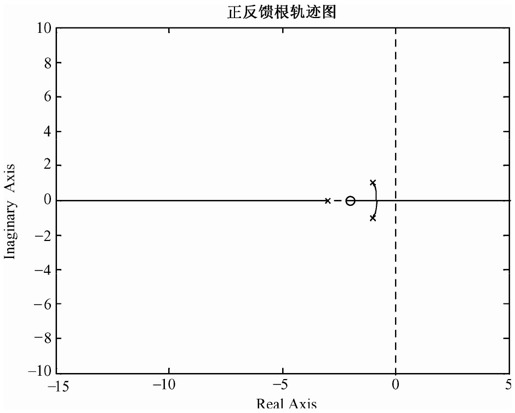
图6.13　例6-6的根轨迹图

【例6-7】　绘制参数a的根轨迹。已知某单位负反馈系统的开环传递函数为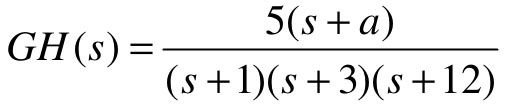165-6，其中2≤a≤10，试使用MATLAB画出系统的根轨迹。

解：MATLAB程序代码如下。

  1. k=5 ;  den=conv(conv([1 1], [1 3]), [1 12]);  %传递函数分母多项式系数
  2. clpoles=[];   param=[];         %定义数组存储结果
  3. for alpha=2:10                  %a从2变化到10
  4. num=[0,0,k,k*alpha];
  5. clpoly=num+den;
  6. clp=roots(clpoly);              %计算闭环极点
  7. clpoles=[clpoles; clp'];  param=[param;alpha];
  8. end
  9. disp([param, clpoles])          %打印a和极点表格
  10. plot(clpoles, '*')              %绘制极点
  11. axis equal;                     %对x轴和y轴采用相同的单位长度
  12. axis([-4,0,-2,2])               %调整绘制区域
  13. title('参数根轨迹图')       %添加图标题

根轨迹图如图6.14所示。

167-1

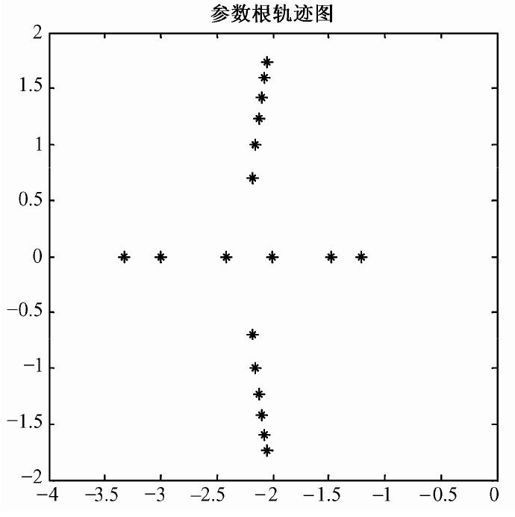
图6.14　例6-7的根轨迹图

【例6-8】　绘制时滞系统的根轨迹。已知某单位负反馈系统的开环传递函数为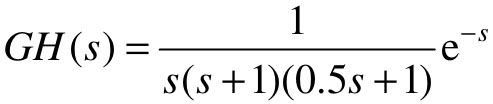166-2，试使用MATLAB画出系统的根轨迹。

解：MATLAB程序代码如下。

  1. num=[0, 1];  den=conv(conv([1 0], [1 1]), [0.5 1]);
  2.                                %传递函数分子、分母多项式系数行向量
  3. sys1=tf(num, den)              %建立传递函数模型
  4. [np, dp]=pade(1, 3);           %对时滞环节进行Pade近似
  5. sys=sys1*tf(np, dp)            %建立系统的传递函数
  6. rlocus(sys)                    %绘制根轨迹图
  7. title('时滞系统的根轨迹图')    %添加图标题

运行程序，输出结果如图6.15所示。

167-2

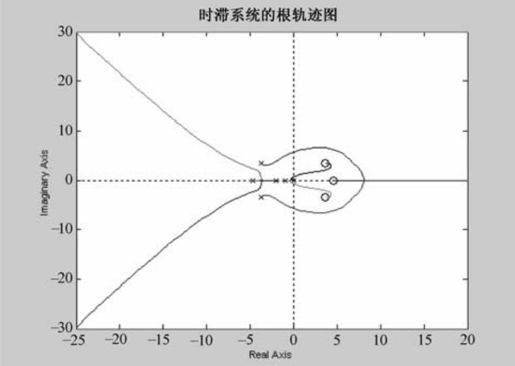
图6.15　例6-8的根轨迹图