6.3　根轨迹法基础

当今，在计算机上绘制根轨迹已经是很容易的事，尤其是使用MATLAB来绘制根轨迹。计算机绘制根轨迹大多采用直接求解特征方程的方法，也就是每改变一次增益K就求解一次特征方程。让K从零开始等间隔增大，只要K的取值足够多、足够密，相应解特征方程的根就在S平面上绘出根轨迹。

传统的根轨迹法是不直接求解特征方程的，它创造了一套行之有效的办法——图解加计算的手工绘图法。如今，尽管手工绘制根轨迹的一些繁琐技艺已经没有多大价值，但是它所发掘出来的根轨迹基本规律，无论用哪种方法作图都是适用的。下面介绍根轨迹最基本、最重要的规律：幅值条件和相角条件。

6.3.1　幅值条件和相角条件

假设控制系统如图6-1所示。

153-1

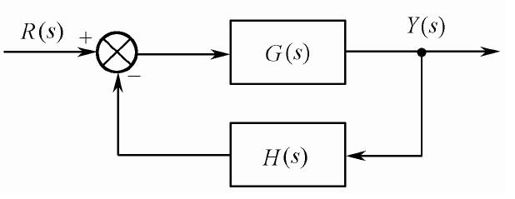
图6.1　控制系统框图

图中G(s)是前向通道的传递函数，表示为：

153-2

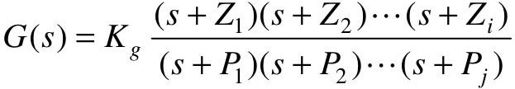
H(s)是反馈通道的传递函数，表示为：

153-3

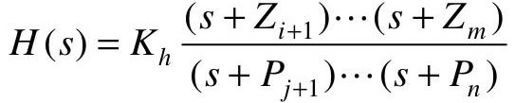
反馈通道通常假定为负反馈形式，除非另有说明。

根据上述通道的传递函数，可求得系统闭环传递函数为：

153-4

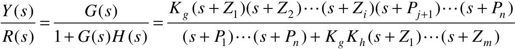
从闭环传递函数式可知，闭环零点：-Z1,…,-Zi和-Pj+1,…,-Pn分别是前向通道传递函数G(s)的零点和反馈通道传递函数H(s)的极点，这可从前向通道和反馈通道传递函数中直接得到。

闭环极点可以从求解下列闭环特征方程D(s)中得到：

153-5

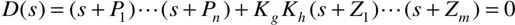
D(s)是一个高阶代数方程，甚至没有解析解，求根很不方便，而且直接求根不容易看出闭环极点和系统参数之间的关系，也就是说，从系统参数很难看出它对系统性能的影响。

采用根轨迹法时，把闭环特征方程D(s)写成另一种等价形式，见式（6-1），称为根轨迹方程。

153-6

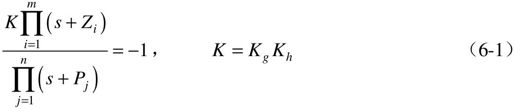
一般意义上的根轨迹，即上述方程在开环增益K从0→∞变化时，闭环极点在复S平面内的变化情况（其中S=σ+jω），也就是180°根轨迹。

为了便于用于图法求取根轨迹方程的解，把式（6-1）分解成幅值和相角两个方程，分别称为幅值条件和相角条件。

幅值条件：

154-1

相角条件：

154-2

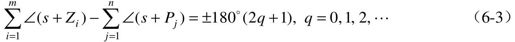
满足幅值条件和相角条件的所有s值，就是特征方程的根，也就是闭环极点。例如，对于一个开环系统，Pi(i=1,2,3,4)是开环系统的极点，z1是开环系统的零点，如图6.2所示，对于S平面上的试验点s，如果它在根轨迹上，就应当满足以下相角条件：

154-3

154-4

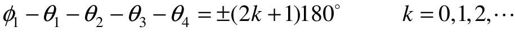
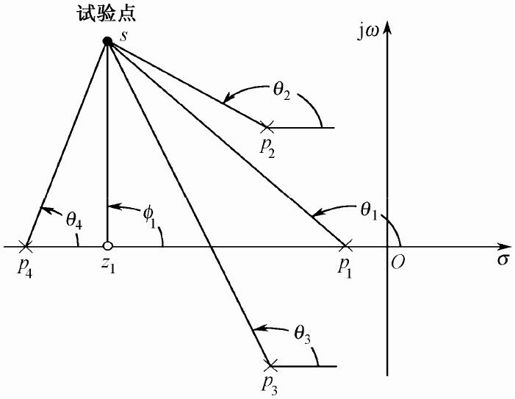
图6.2　相角条件的图示

量出或计算出上述5个角度，就知道试验点s是否在根轨迹上。

因为K在0→∞范围内连续变化，总有一个K值能满足幅值条件，因此绘制根轨迹的依据是相角条件，即特征方程的所有根都应满足式（6-3），即相角的和应等于±180°(2q+1)。换句话说，在S平面内所有满足式（6-3）的s点都是系统的特征根，这些点的连线就是根轨迹。

6.3.2　绘制根轨迹的一般法则

显然，用图解分析法来绘制根轨迹图是不方便的，于是发展了一套用于在复平面上快速确定根轨迹基本走向和特殊点（区域）的方法。由此，可以快速地在复平面上画出根轨迹图，这些图在特殊点（区域）上是准确的，其余部分是近似的，可用相角条件来局部准确化。这些方法在系统分析中的另一重要作用是可以从系统的开环零极点分布情况，快速地估计出闭环根轨迹的走向。以下就是这些基本法则。

（1）法则1：根轨迹的分支数、连续性和对称性。

根轨迹的分支数等于闭环特征方程式的阶次，一般情况下等于开环极点数。根轨迹在复平面上是一簇连续的曲线，并对称于实轴。因为根轨迹是闭环特征方程的根，特征方程的根是实根（在实轴上）或者是共轭复根（对称于实轴），所以根轨迹一定对称于实轴。

（2）法则2：根轨迹的起点和终点。

根轨迹起始于开环极点，终止于开环零点。如果开环极点数和零点数不等，则其余的根轨迹不是终止于无穷远处，就是起始于无穷远处。

因为根轨迹是闭环特征方程的根，当K=0时方程的根就是它的n个开环极点，当K→∞时方程的根就是它的m个开环零点。根轨迹的起点和终点是根轨迹的特殊点。当n=m时，开始于n个开环极点的n支根轨迹正好终止于m个开环零点。

当n>m时，开始于n个开环极点的n支根轨迹，有m支终止于开环零点，有n-m支终止于无穷远处。这时，无穷远处也称为“无穷远零点”。

当n<m时，终止于m个开环零点为m支根轨迹，有n支来自n个开环极点，有m-n支来自无穷远处。必须指出，实际系统极少有n<m的情况，但是在处理特殊根轨迹时，常常将系统特征方程变形，变形后的等价系统可能会出现这种情况。

（3）法则3：位于实轴上的根轨迹。

若实轴段右侧开环极点和开环零点数之和为奇数，则实轴段为根轨迹或根轨迹的一部分，如图6.3所示。

155-1

图6.3　位于实轴上的根轨迹

（4）法则4：趋于无穷远的根轨迹的渐近线。

趋于无穷远的根轨迹的渐近线均交于实轴上，实轴交点坐标为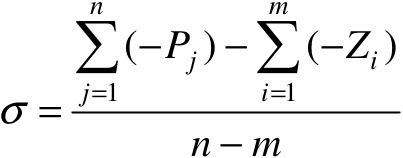155-2。

渐近线与正实轴的夹角为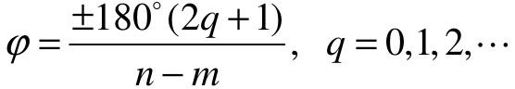155-3。

（5）法则5：根轨迹的分离点和会合点。

当K从0变到无穷大时，根轨迹可能先会合后分离，这样的点称分离点。分离点对应重闭环极点。

显然，位于实轴上的两个相邻的开环极点之间一定有分离点，因为任何一条根轨迹不可能开始于一个开环极点而终止于另一个开环极点。同理，位于实轴上的两个相邻的开环零点之间也一定有分离点。

当然，分离点也可以是复数，两个相邻的开环复极点（或零点）之间可能有分离点。由根轨迹方程可得分离点和会合点的求解公式如下：

156-1

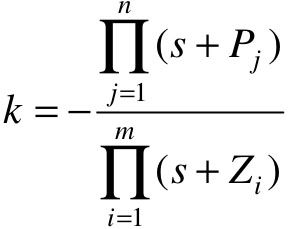
根轨迹分离点和会合点坐标满足方程dk/ds=0。

（6）法则6：根轨迹的起始角和终止角。

根轨迹从开环极点出发的方位角（起始角）为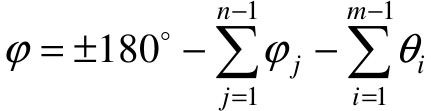：156-2，其中，φj是其他开环极点到该极点的方位角，θi是开环零点到该极点的方位角。

根轨迹终止于开环零点的方位角（终止角）上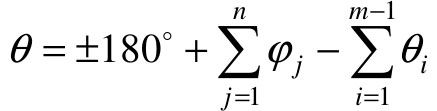：156-3，其中，φj是其他开环极点到该零点的方位角，θi是开环零点到该零点的方位角。

（7）法则7：根轨迹与虚轴交点坐标。

系统闭环特征方程为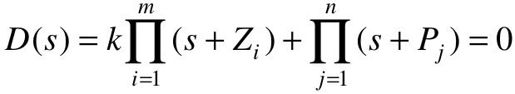：156-4。交点满足方程D(jω)=0。

（8）法则8：根轨迹上任一点所对应的根轨迹增益为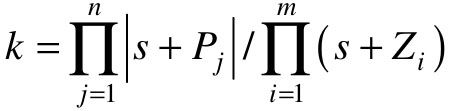156-5。

6.3.3　与根轨迹分析相关的MATLAB函数

在MATLAB中，对于如图6-1所示的n阶单输入单输出系统，采用函数pzmap( )绘制系统零极点，通过输入“rlocus(GH)”可得根轨迹图，它描绘了当开环增益K从0→∞变化时，闭环极点在复S平面内的变化情况，即系统GH的180°根轨迹。MATLAB会计算出根轨迹的n条分支，并以其选定的实轴和虚轴绘制图形。

值得注意的是，绘制根轨迹时，应令S平面实轴和虚轴的比例尺相同，只有这样才能正确反映S平面上坐标位置与相角的关系，在MATLAB中，通过“axis equal”命令使实轴和虚轴的比例尺保持相同。

在画出根轨迹后，可交互地利用rlocfind命令来确定用户鼠标所点之根轨迹上任意点对应的K值，K值所对应的所有闭环极点值也可以利用形如[K, poles]=rlocfind(GH)的命令来显示。

0°根轨迹对应于图6-1中的正反馈或者开环增益K为负值的情形。在传递函数前面插入一个负号，使用命令rlocus(-GH)即可绘制系统GH的0°根轨迹。

下面介绍与根轨迹分析相关的MATLAB函数。

  1. 绘制零极点的函数pzmap( )

常用的调用格式为：

  1. pzmap(sys);    pzmap(sys1, sys2,…);    [p, z] = pzmap(sys)

使用说明：

  • pzmap()可绘出线性时不变（LTI）系统的零极点图。对单输入单输出（SISO）系统而言，绘制传递函数的零极点；对多输入多输出（MIMO）系统而言，绘制系统的特征矢量和传递零点。
  • pzmap(sys)计算线性时不变（LTI）系统的零极点，并把零极点绘制在复平面上。
  • pzmap(sys1, sys2,…)可在同一个复平面中画出多个LTI系统的零极点，为区分各个系统的零极点，可以用不同的颜色来显示，如pzmap(sys1, 'r', sys2, 'y', sys3, 'g')。
  • [p, z]=pzmap(sys)返回系统零极点位置的数据，而不直接绘制零极点图，如果需要绘制零极点图可以再用pzmap(z, p)函数来实现。
  1. 绘制根轨迹的函数rlocus( )

常用的调用格式为：

  1. rlocus(sys);  rlocus(sys, k);  rlocus(sys1, sys2,…);  [r, k] = rlocus(sys);  r = rlocus(sys, k)

使用说明：

  • rlocus()函数计算并绘制SISO系统的根轨迹。根轨迹用于研究改变反馈增益对系统极点分布的影响，从而进行系统时域和频域响应的分析。rlocus( )函数既适用于连续时间系统，也适用于离散时间系统。
  • rlocus(sys, k)绘制增益为k时的闭环极点。
  • rlocus(sys1, sys2,…)在同一个复平面中画出多个SISO系统的根轨迹，为区分各个系统的根轨迹，可以用不同的颜色和线型来显示，如rlocus(sys1, 'r', sys2, 'y:', sys3, 'gx')。
  • [r, k]=rlocus(sys)或者r=rlocus(sys, k)返回增益为k时复根位置的矩阵R, R有length(k)行，其第j行列出的是增益k(j)时的闭环根。

157-1

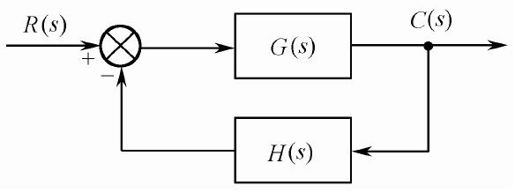
图6.4　反馈控制系统结构图

  1. 计算给定一组根的根轨迹增益的函数rlocfind( )

常用的调用格式为：

  1. [k, poles] = rlocfind(sys);  [k, poles] = rlocfind(sys, p)

使用说明：

  • rlocfind( )函数可计算出与根轨迹上极点相对应的根轨迹增益，它适用于连续时间系统和离散时间系统。
  • [k, poles]=rlocfind(sys)执行后，在根轨迹图形窗口中显示十字形光标，当用户在根轨迹上选择一点时，其相应的增益由k记录，与增益相关的所有极点记录于poles中。
  • [k, poles]=rlocfind(sys, p)函数可对指定根计算对应的增益与根矢量p。
  1. 在连续系统根轨迹图上加等阻尼线和等自然振荡角频率线的函数sgrid( )

常用的调用格式为：

  1. sgrid();  sgrid(z, wn)

使用说明：

  • sgrid( )函数命令可在连续系统的根轨迹或零极点图上绘制出栅格线，栅格线由等阻尼系数与自然振荡角频率构成。阻尼线的间隔为0.1，范围从0到1，自然振荡角频率的间隔为1 rad/s,范围从0到10。
  • 在绘制栅格线之前，当前窗口必须有连续时间系统的根轨迹或零极点图，或者该函数必须与函数pzmap( )或rlocus( )一起使用。
  • sgrid(z, wn)函数可以指定阻尼系数z与自然振荡角频率wn。
  1. 在离散系统根轨迹图上加等阻尼线和等自然振荡角频率线的函数zgrid( )

常用的调用格式为：

  1. zgrid();  grid(z, wn)

使用说明：

  • zgrid( )函数可在离散系统的根轨迹或零极点图上绘制出栅格线，栅格线由等阻尼系数与自然振荡角频率构成。阻尼线的间隔为0.1，范围从0到1，自然振荡角频率的间隔为pi/10，范围从0到pi。
  • 在绘制栅格线之前，当前窗口必须有离散时间系统的根轨迹或零极点图。
  • zgrid(z, wn)函数可以指定阻尼系数z和自然振荡角频率wn。

6.3.4　根轨迹分析与设计工具rltool

MATLAB控制系统工具箱提供了一个系统根轨迹分析与设计的工具rltool。使用rltool，可以方便地绘制系统的根轨迹，已经使用根轨迹校正法对系统进行校正。

下面先简要介绍rltool的组成及基本操作，本书的后续内容中将使用这一工具进行系统的分析和设计。

在MATLAB命令窗口中输入“rltool”就可以激活根轨迹设计GUI窗口，如图6.5所示。

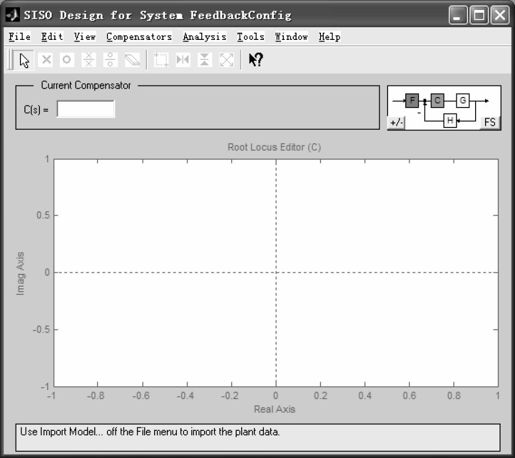
158-01

图6.5　rltool根轨迹设计GUI窗口

rltool根轨迹设计GUI界面由以下几个主要的部分组成。

  • 补偿器描述区：给出了当前补偿器的结构，默认值为C(s)=1。
  • 反馈结构图区：给出当前系统的整体框图，其中F为前滤波器，G为控制对象模型，C为补偿器，H为反馈环节。
  • 根轨迹工具条：其中的按钮用来增加或者删除补偿器的零极点，还可以通过鼠标完成零极点的摆放。
  • 绘图区：用于显示系统的根轨迹。

rltool是图形化的交互式工具，可以打开工作空间中的单输入单输出（SISO）系统模型，分析其根轨迹，并且允许用户在根轨迹图上直接放置/删除需要的零极点，完成对系统的校正设计。

例如，对于单位负反馈控制系统的开环传递函数为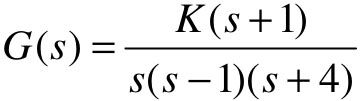159-1，在MATLAB工作空间中建立其模型的程序如下：

  1. num = [1 1];          　　　　　　　　　 % 开环传递函数分子多项式系数
  2. den = conv([1 0],conv([1-1],[1 4]));   % 开环传递函数分母多项式系数
  3. sys = tf(num,den)         　　　　　　　% 控制系统的开环传递函数模型

生成sys模型后，执行命令“rltool(sys)”，就可以得到控制系统sys的根轨迹分析图形界面，如图6.6所示。

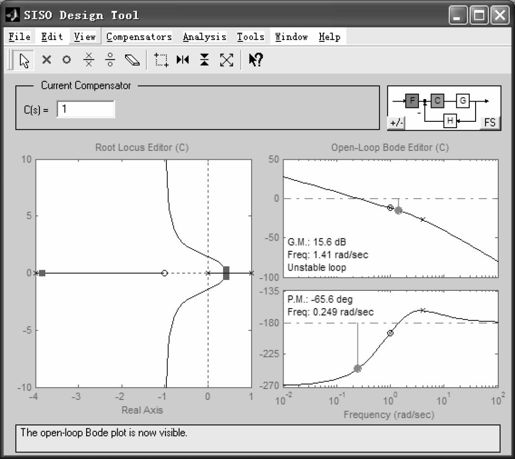
159-01

图6.6　控制系统根轨迹分析与设计器

其中，Root Locus Editor是根轨迹编辑器，上方的Current Compensator用来设定系统的增益值，右边的Open-Loop Bode Editor则是系统的开环Bode图。在根轨迹上拖曳鼠标，可以得到相应的系统增益、相角稳定裕度、穿越频率、剪切频率等参数。

在Current Compensator编辑器中输入不同的值，Root Locus Editor中会立刻显示出对应的极点。设定系统增益为6，根轨迹和Bode图如图6.7所示。

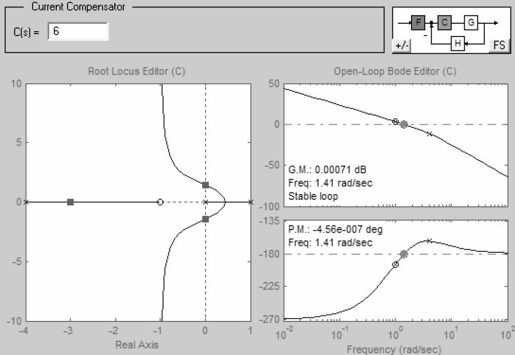
160-01

图6.7　设定系统增益为6时的根轨迹和Bode图

从图中不难看出，K=6恰好是系统的临界增益，这与rlocfind命令得出的结果是相符的。利用rltool还可以在根轨迹图中增加、删除系统的零极点，非常方便。

6.3.5　利用MATLAB绘制根轨迹图举例

下面通过几个例子，讲述MATLAB在绘制根轨迹图中的应用。

【例6-1】　已知某系统的闭环传递函数为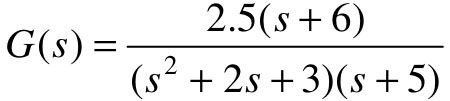159-2，试使用MATLAB画出系统的零极点，并求出系统的零极点。

解：MATLAB程序代码如下。

  1. num=2.5*[1, 6];  den=conv([1, 2, 3], [1, 5]);
  2.                          %传递函数分子、分母多项式系数行向量
  3. sys=tf(num, den)         %建立传递函数模型
  4. pzmap(sys)               %绘制零极点图
  5. [p, z]=pzmap(sys)        %输出零极点
  6. title('零极点图')        %添加图标题

程序运行后，输出零极点图，如图6.8所示。输出系统的闭环极点p和零点z如下：

  1. p = -5.0000
  2.   -1.0000 + 1.4142i
  3.   -1.0000 - 1.4142i
  4. z = -6

160-2

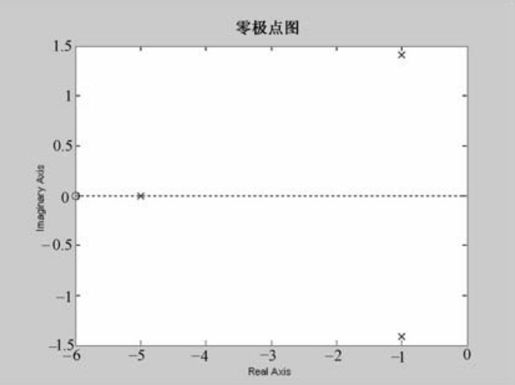
图6.8　例6-1的闭环零极点分布图

【例6-2】　已知单位负反馈系统，系统的开环传递函数为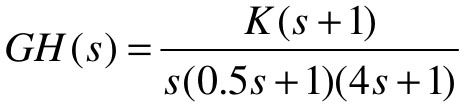160-3，试使用MATLAB绘制系统的根轨迹。

解：MATLAB程序代码如下。

  1. num=[1, 1];  den=conv([1, 0], conv( [0.5, 1], [4, 1]) );
  2.                         %传递函数分子、分母多项式系数
  3. sys=tf(num, den)        %建立传递函数模型
  4. rlocus(sys)             %绘制根轨迹图
  5. title('根轨迹图')       %添加图标题

程序运行后可得如图6.9所示的根轨迹。

161-1

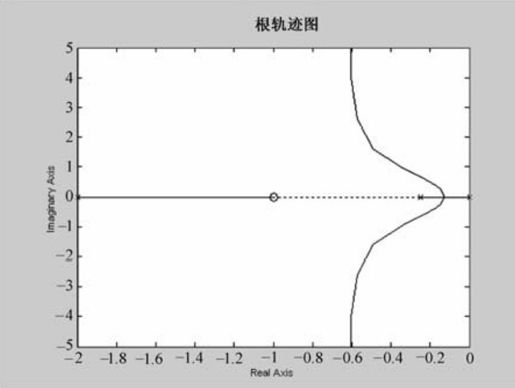
图6.9　例6-2的根轨迹图

【例6-3】　已知某单位负反馈系统的开环传递函数为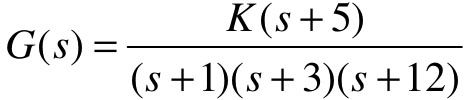161-2，试使用MATLAB绘制系统的根轨迹，并在根轨迹图上任选一点，计算该点的增益K及其所有极点的位置。

解：MATLAB程序代码如下。

  1. num=[1, 5]; den=conv([1, 1], conv( [1, 3], [1, 12]) );
  2.                       %传递函数分子、分母多项式系数行向量
  3. sys=tf(num, den)      %建立传递函数模型
  4. rlocus(sys)           %绘制根轨迹图
  5. [k, poles]=rlocfind(sys)  %计算用户所选定的点处的增益和其他闭环极点
  6. title('根轨迹图')         %添加图标题

程序运行后输出如图6.10所示的根轨迹图，并在图形窗口中显示十字形光标，当用鼠标左键在根轨迹图上选择一点时，就可得到该点对应的增益K，以及该K值下其他的极点，所有的极点在图中以‘+’表示。

例6-3的程序运行结果如下。

  1. Select a point in the graphics window  %以十字形光标提示在图形窗口的根轨迹上选择一点
  2. selected_point =%选择以下点
  3.   -4.3294 + 5.0311i
  4. %计算输出该店对应的增益k和该k值下其他的极点poles
  5. k = 56.7396
  6. poles = -7.2050
  7.   -4.3975 + 5.0034i
  8.   -4.3975 - 5.0034i

运行结果如图6.10所示。

162-1

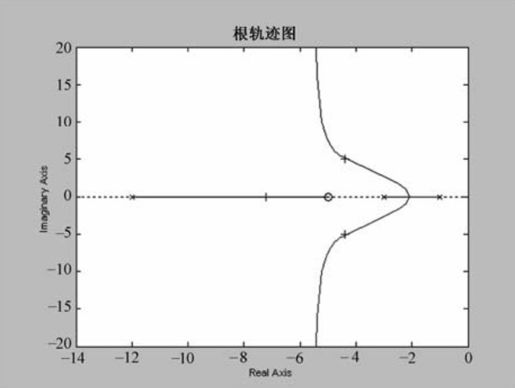
图6.10　例6-3的根轨迹图

由程序执行结果可知，当K=56.7396时，该单位负反馈系统的三个闭环极点是

162-2

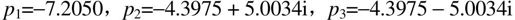
【例6-4】　已知某单位负反馈系统的开环传递函数为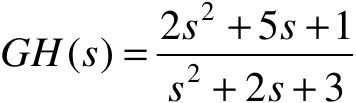162-3，试使用MATLAB画出带栅格线的根轨迹图。

解：MATLAB程序代码如下。

  1. num=[2, 5, 1];  den=[1, 2, 3];  %传递函数分子、分母多项式系数行向量
  2. sys=tf(num, den)    %建立传递函数模型
  3. rlocus(sys)         %绘制根轨迹图
  4. sgrid               %绘制出由等阻尼系数与自然振荡角频率组成的栅格线
  5. title ('带栅格线的根轨迹图')    %添加图标题

程序运行后得到如图6.11所示的根轨迹。

162-4

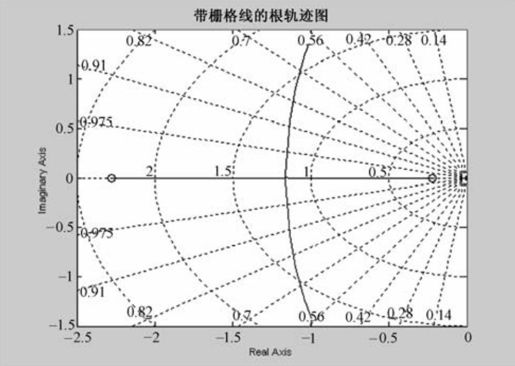
图6.11　例6-4带栅格线的根轨迹图

【例6-5】　已知某单位负反馈系统的开环传递函数为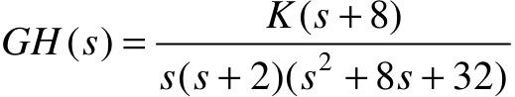163-1，试使用MATLAB画出根轨迹图，并分析不同的根轨迹特性的适用范围，结合绘制根轨迹的规则，计算GH(s)离开上部复极点的角度，并与MATLAB绘制的图形进行比较。

求下面两种情况下的K值：

（1）两条分支进入右半平面时；

（2）两条分支从复数极点出发在实轴相交时。

解：MATLAB程序代码如下。

  1. num=[1, 8];   den=conv([1, 2, 0], [1, 8, 32]);
  2.                             %传递函数分子、分母多项式系数行向量
  3. sys=tf(num, den)            %建立传递函数模型
  4. rlocus(num, den)            %计算根轨迹图
  5. axis([-15 5 -10 10])        %调整绘制区域
  6. [k, poles]=rlocfind(sys)    %计算增益值和极点
  7. title('根轨迹图')           %添加图标题

MATLAB绘制的根轨迹如图6.12所示。

163-2

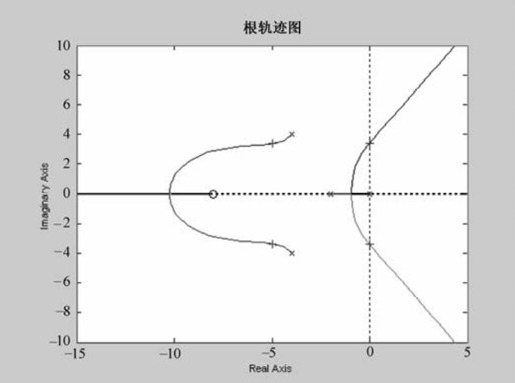
图6.12　例6-5的根轨迹图

可以看到，实轴部分是σ≤8和-2≤σ≤0（对应法则3），根轨迹有4条分支（对应法则1），分别从开环极点s=0, -2, -4+j4和-4-j4发出，其中1条分支终止于开环零点s=-8处，另外3条分支趋近60°, -180°的3条渐近线（对应法则2、法则4），它们的渐近线在点σ0=[(0-2-4-4)-(-8)]/(4-1)=-2/3处相交（对应法则5）。

出射角（对应法则6）可由以上复数极点算出。首先，可任意指定p1=-4+j4, p2=-4-j4, p3=-0, p4=-2，z1=-8，然后利用式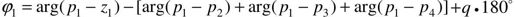163-3，代入零点和极点值，可求得出射角为-116.6°。

还可以做进一步分析，由于开环极点的数目至少比开环零点的数目多两个，当K变化时，闭环极点之和始终为一常数。对于K=0时，其和为0-2-4-4=-10，因此对所有的K值，4个闭环极点的和为-10。因此当两个复数分支穿过虚轴时，其他两个闭环极点的实部必定等于-5。从根轨迹图可以看出这两个闭环极点为s≈-5±j3.5。

利用rlocfind命令，可求得当K≈45时，从实数极点上出发的两条分支穿入右半平面；当K≈2070时，从复数极点出发的两条分支到达实轴。

从以上例子可以看出，熟练掌握和运用绘制根轨迹图的MATLAB函数，读者能简化根轨迹的绘制工作，从而把重点放在根轨迹图的分析和理解上。