13.5 综合实例及MATLAB/Simulink应用
下面通过几个综合实例,讲述MATLAB/Simulink在本章中的应用。
【例13-1】 给定系统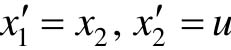 。求最优控制,使性能指标
。求最优控制,使性能指标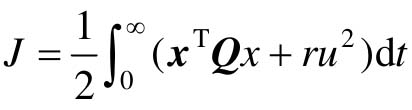 取极小值。性能指标中,
取极小值。性能指标中,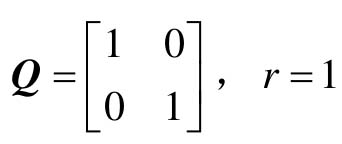 ,r=1。
,r=1。
解:利用MATLAB求解的基本步骤如下。
【步骤1】 建立系统的模型。
首先建立给定控制系统的数学模型,MATLAB代码如下:
- clc; % 清除窗口显示
- clear; % 清除工作空间所有变量
- A = [0 1;0 0]; B = [0 ; 1]; C = [1 0]; D = [0]; %系统的状态空间矩阵
- sys = ss(A,B,C,D) % 建立控制系统的状态空间模型
【步骤2】 判断系统的可控性和可观性。
根据建立的控制系统状态空间模型,计算系统的可控矩阵,判断其可控性。
MATLAB代码如下:
- control = ctrb(A,B) % 计算系统的可控矩阵
- if rank(control) ==2 % 如果系统的可控矩阵满秩
- disp('系统是完全能控的!'); % 说明系统的完全能控的
- else % 如果不满秩
- disp('系统是不完全能控的!'); % 说明系统不完全能控
- end
程序运行结果为:
- control = 0 1
- 1 0
- 系统是完全能控的!
其次,还可以将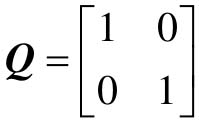 分解为
分解为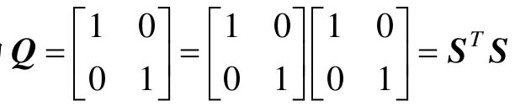 。计算相应的能观矩阵,代码如下:
。计算相应的能观矩阵,代码如下:
- s = [1 0; 0 1]; observe = [s ; s * A] % 计算能观矩阵
程序运行的结果为:
- observe = 1 0
- 0 1
- 0 1
- 0 0
矩阵的秩为2,系统能改。因此,可以设计最优反馈调节器,并且使得闭环后的系统稳定。
【步骤3】 计算线性二次型最优控制的解。
根据建立好的系统模型,利用lqr函数计算线性二次型最优控制的解。
MATLAB代码如下:
- % 最优控制与最优性能的求解
- R = 1; Q = [1 0; 0 1]; [K,P,E] = lqr(A,B,Q,R) % 计算最优状态反馈的解
程序运行的结果为:
- K = 1.0000 1.7321
- P = 1.7321 1.0000
- 1.0000 1.7321
- E = -0.8660 + 0.5000i
- -0.8660 - 0.5000i
也就是说,最优的状态反馈为K=[1 1.7321]。因此,系统的最优控制为u=-Kx=-x1-1.7321x2。
【步骤4】 分析闭环系统的特性。
下面进一步讨论闭环系统的特性。引入状态反馈后,系统的状态转移矩阵变为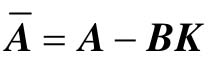 。利用MATLAB建立闭环系统的数学模型,并且比较反馈前后系统的稳定性。代码如下:
。利用MATLAB建立闭环系统的数学模型,并且比较反馈前后系统的稳定性。代码如下:
- A_new = A - B * K; % 反馈后系统的状态矩阵
- sys_new = ss(A_new,B,C,D) % 建立闭环控制系统的数学模型
- figure(1) % 开启新的图形窗口
- step(sys); % 绘制反馈前系统的阶跃响应曲线
- gtext('反馈前') % 给曲线添加标注
- figure(2) % 开启新的图形窗口
- step(sys_new); % 绘制反馈后系统的阶跃响应曲线
- gtext('反馈后') % 给曲线添加标注
程序运行的结果为:
- % 闭环系统的状态空间表示
- a = x1 x2
- x1 0 1
- x2 -1 -1.732
- b = u1
- x1 0
- x2 1
- c = x1 x2
- y1 1 0
- d = u1
- y1 0
对比反馈前后系统的阶跃响应曲线,如图13.1所示。
从图13.1中不难看出,反馈前系统不稳定;通过状态反馈,闭环系统稳定,并且在阶跃响应下的稳态值为1,稳态误差为0。这与步骤2中对系统能控性和能观性的分析结果相符合。
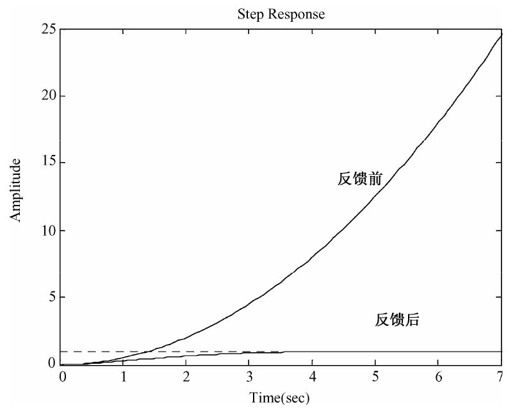
图13.1 对比反馈前后系统的阶跃响应曲线
从步骤3计算得出的E矩阵中也可以分析出闭环系统的稳定性。因为E是闭环系统状态矩阵的特征值,而它们都位于复平面的左半部分,因此系统是稳定的。
【例13-2】 给定离散控制系统如下:
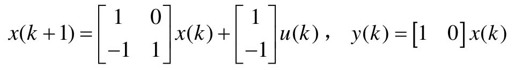
求最优控制,使性能指标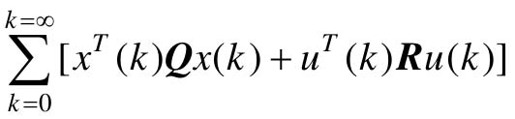 取极小值。式中,
取极小值。式中,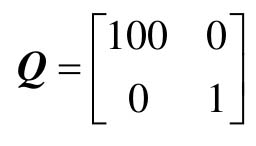 ,R=1。
,R=1。
解:利用MATLAB求解的基本步骤如下。
【步骤1】 建立系统的模型。
首先建立控制系统的数学模型。代码如下:
- clc; % 清除工作窗口中的显示
- clear; % 清除工作空间中的所有变量
- A = [1 0; -1 1]; B = [1; -1]; C = [1 0]; D = [0]; %系统的状态矩阵
- Q = [100 0; 0 1]; R = 1; % 设定指标函数中的Q、R矩阵
- sys = ss(A,B,C,D) % 建立控制系统的状态空间模型
【步骤2】 计算离散线性二次型最优控制的解。
利用MATLAB中的dlqr命令,计算离散线性二次型最优控制的解。代码如下:
- [K,S,E] =dlqr(A,B,Q,R) % 计算最优控制的解
- A_new = A - B * K; % 反馈后系统的状态矩阵
- sys_new =ss(A_new,B,C,D) % 建立反馈后系统的数学模型
程序运行的结果为:
- K = 0.9911 -0.0942
- S = 100.9911 -0.0942
- -0.0942 10.5219
- E = 0.0098
- 0.9049
也就是说,最优的状态反馈矩阵为K=[0.9911 -0.0942]。
同时,系统进行状态反馈后的状态空间模型为:
- a = x1 x2
- x1 0.008873 0.0942
- x2 -0.008873 0.9058
- b = u1
- x1 1
- x2 -1
- c = x1 x2
- y1 1 0
- d = u1
- y1 0
【步骤3】 求取系统反馈前后的阶跃响应。
对比反馈前后系统的阶跃响应。代码如下:
- dstep(A,B,C,D,1,10); % 绘制反馈前系统的阶跃响应曲线
- hold on; % 在同一幅图像上绘制多条曲线
- dstep(A_new,B,C,D,1,10); % 绘制反馈后系统的阶跃响应曲线
- gtext('状态反馈前'); gtext('状态反馈后'); % 给曲线添加标注
程序运行的结果如图13.2所示。
可见,通过状态反馈,使得原先不稳定的系统变得稳定。
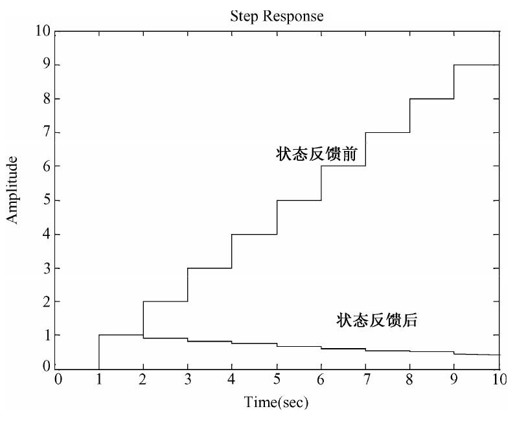
图13.2 状态反馈前后系统的阶跃响应曲线
习 题
【13.1】 已知某受控系统的状态空间表达式为
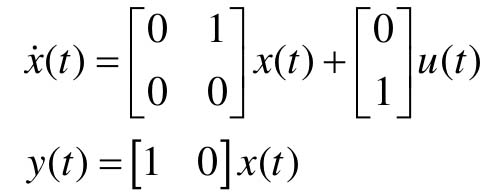
(1)利用MATLAB建立上述控制系统的数学模型;
(2)假定性能指标为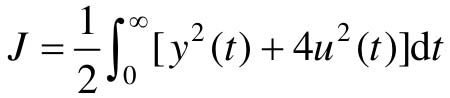 ,计算使系统的性能指标J为极小值时的最优反馈矩阵K;
,计算使系统的性能指标J为极小值时的最优反馈矩阵K;
(3)绘制反馈前后系统的阶跃响应曲线,比较二者的不同。
【13.2】 已知二阶系统的状态空间表达式为

(1)利用MATLAB建立上述控制系统的数学模型;
(2)假定性能指标为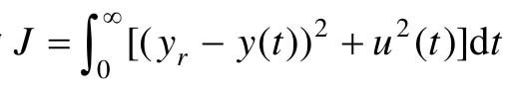 ,给定的预期输出为yr=1(t)。确定使J为极小值时的控制律。
,给定的预期输出为yr=1(t)。确定使J为极小值时的控制律。
【13.3】 给定系统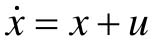 。求最优控制,使性能指标
。求最优控制,使性能指标
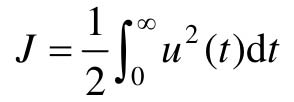
取极小值。
