5.3　MATLAB/Simulink在时域分析中的应用

5.3　MATLAB/Simulink在时域分析中的应用

时域分析，尤其是高阶系统的时域分析，其困难主要在系统极点、留数的获取上，以及在已知响应表达式的基础上，如何绘制响应波形和求取性能指标等一系列问题，这些均涉及大量的数值计算和图形绘制，MATLAB/Simulink的仿真平台为此提供了强有力的工具。

5.3.1　时域分析中MATLAB函数的应用

一个动态系统的性能常用典型输入作用下的响应来描述。响应是指零初始值条件下某种典型的输入函数作用下对象的响应，控制系统常用的输入函数为单位阶跃函数和脉冲激励函数（即冲激函数）。

5.3.1.1　MATLAB中常用的时域分析函数

在MATLAB中，提供了求取连续系统的单位阶跃响应函数step()，单位脉冲响应函数impulse()，零输入响应函数initial()及任意输入响应函数lsim()。下面分别进行介绍。

单位阶跃响应函数step()

函数step()将绘制出由向量num和den表示的连续系统的阶跃响应g(t)在指定时间范围内的波形图，并能求出其数值解。

单位阶跃响应函数step()的常见用法有：

y=step(num, den, t)：其中num和den分别为系统传递函数描述中的分子和分母多项式系数，t为选定的仿真时间向量，一般可由t=0:step:end等步长地产生。该函数返回值y为系统在仿真中所得输出组成的矩阵。
[y, x, t]=step(num, den)：时间向量t由系统模型特性自动生成,状态变量x返回为空矩阵。
[y, x, t]=step(A, B, C, D, iu)：其中A, B, C, D为系统的状态空间描述矩阵，iu用来指明输入变量的序号，x为系统返回的状态轨迹。

如果对具体的响应值不感兴趣，而只想绘制系统的阶跃响应曲线，则可采用step(num, den)、step(num, den, t)、step(A, B, C, D, iu, t)和step(A, B, C, D, iu)的格式进行函数调用。

线性系统的稳态值可以通过控制系统工具箱中的函数dcgain()来求得，其调用格式为dc=dcgain(num, den)或dc=dcgain(a, b, c, d)。

单位脉冲响应函数impulse()

函数impulse()将绘出由向量num和den表示的连续系统在指定时间范围内的脉冲响应h(t)的时域波形图，并能求出指定时间范围内脉冲响应的数值解。

与step()函数一样，impulse()函数也有以下用法：

y=impulse(num, den, t)
[y, x, t]=impulse(num, den)
impulse(num, den)和impulse(num, den, t)
[y, x, t]=impulse(A, B, C, D, iu, t)
impulse(A, B, C, D, iu)和impulse(A, B, C, D, iu, t)

零输入响应函数initial()

MATLAB的控制系统工具箱提供了求取连续系统零输入响应的函数initial()，其常用的格式有：

initial(sys,x0)和initial(sys,x0,t)
[Y,T,X]=initial(sys,x0)和[Y,T,X]=initial(sys,x0,t)

说明：sys为线性时不变系统的模型，x0为初始状态，t为指定的响应时间，Y为响应的输出，T为仿真的时间，X为系统的状态变量。

说明：initial()函数可计算出连续时间线性系统由于初始状态引起的响应（故称零输入响应）。

当不带输出变量引用函数时，initial()函数在当前图形窗口中直接绘制出系统的零输入响应曲线。

当带有输出变量引用函数时，可得到系统零输入响应的输出数据，而不直接绘制出曲线。

任意输入响应函数lsim()

MATLAB的控制系统工具箱提供了求取任意输入响应函数lsim()，其常用的格式有：

lsim(sys1,u,t)和lsim(sys2,u,t,x0)
[Y,T,X]=lsim(sys1,u,t)和[Y,T,X]=lsim(sys2,u,t,x0)

说明：u为输入信号，x0为初始条件，t为等间隔时间向量，sys1为tf()或zpk()模型，sys2为ss()模型。Y为响应的输出，T为仿真的时间，X为系统的状态变量。

当不带输出变量引用函数时，lsim()函数在当前图形窗口中直接绘制出系统的零输入响应曲线。

当带有输出变量引用函数时，可得到系统零输入响应的输出数据，而不直接绘制出曲线。

对于离散系统，只需在连续系统对应函数前加“d”即可，如dstep，dimpulse等，其调用格式与step、impulse类似，后面章节将会讲到。

5.3.1.2　时域响应应用举例

下面通过实例讲述利用上述函数求取系统的时域响应。

【例5-1】　已知系统的闭环传递函数为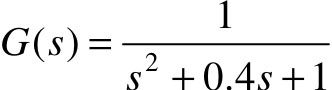 119-1 ，试求其单位阶跃和单位斜坡响应曲线。

解：MATLAB程序代码如下。

num=[1];   den=[1, 0.4, 1];              %传递函数分子、分母多项式系数行向量
t=[0:0.1:10]                             %响应时间
u=t;                                     %u为单位斜坡输入
y=step(num, den, t)                      %单位阶跃响应
y1=lsim(num, den, u, t)                  %单位斜坡响应
plot(t, y,'b-',t, y1,'r:')               %将两条响应曲线绘制在同一个图上
grid                                     %添加栅格
xlabel('Time [sec] t') ; ylabel('y')     %标注横、纵坐标轴
title('单位阶跃和单位斜坡输入响应曲线')        %添加图标题
legend('单位阶跃响应曲线','单位斜坡响应曲线')  %添加文字标注

运行程序，输出的响应曲线如图5.9所示。

120-1

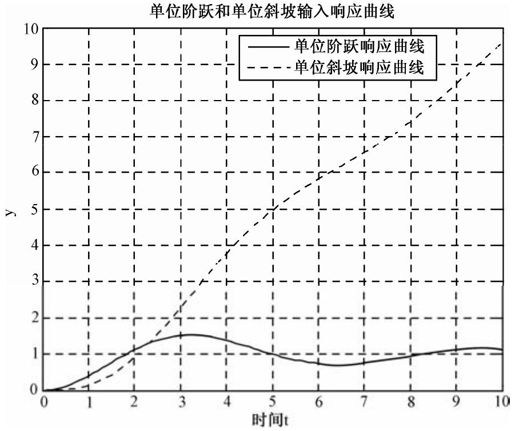
图5.9　例5-1的响应曲线

【例5-2】　已知单位负反馈系统，其开环传递函数为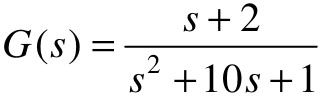 121-2 ，系统输入信号为如图5.10所示的三角波，试求取系统输出响应，并将输入输出信号对比显示。

120-2

图5.10　例5-2输入曲线

解：MATLAB程序代码如下。

numg=[1, 2];  deng=[1, 10, 1];        %开环传递函数分子、分母多项式系数行向量
[num, den]=cloop(numg, deng, -1)      %建立单位负反馈传递函数
v1=[0:0.1:1];  v2=[0.9:-0.1:-1]; v3=[-0.9:0.1:0]; u=[v1, v2, v3]   %产生三角波
t=[0:0.1:4]                           %仿真时间
[y, x]=lsim(num, den, u, t)           %求取系统在三角波输入下的响应
plot(t, y, t, u);  grid  %将输入的三角波和输出的响应曲线绘在在同一个图上，并添加栅格
xlabel('Time [sec] t');  ylabel('y'); %标注横、纵坐标轴
title('三角波输入和输入下的响应曲线') %添加图标题
legend('响应曲线','三角波输入')       %添加文字标注

响应曲线如图5.11所示。

120-3

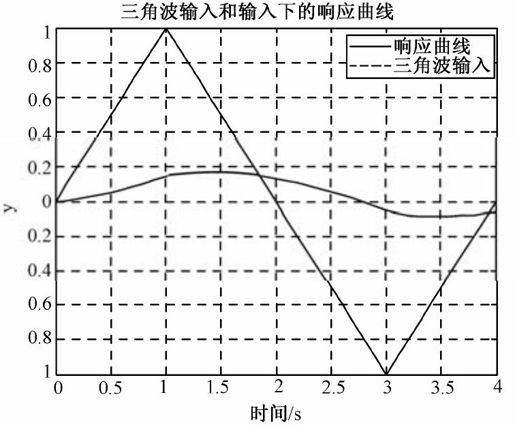
图5.11　例5-2的响应曲线

【例5-3】已知单位负反馈系统，其开环传递函数为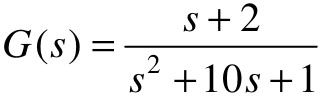 121-2 ，系统输入信号为如图5.12所示的锯齿波，试用Simulink求取系统输出响应，并将输入输出信号对比显示。

121-3

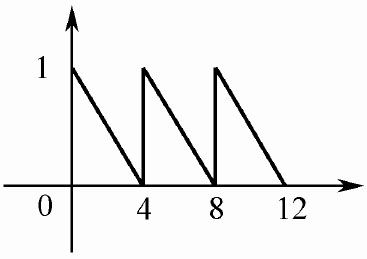
图5.12　例5-3输入曲线

解：使用Simulink可以方便地实现对系统的建模和仿真，Simulink的模型如图5.13所示。

121-4

图5.13　例5-4的Simulink模型

图5.13中，“Transfer Fcn”模块建立G(s)的模型，“Signal Generator”产生输入的锯齿波，其参数设置如图5.14所示。按照题意，设置时在“Wave form”中选中“sawtooth”（锯齿波），在“Amplitude”（幅值）中输入1，在“Frequency”中输入1/4，在“Units”（单位）选中“Hertz”（赫兹）。Simulink中还提供了其他类型的信号发生器，其使用方法和本题类似，这里不做详细介绍。

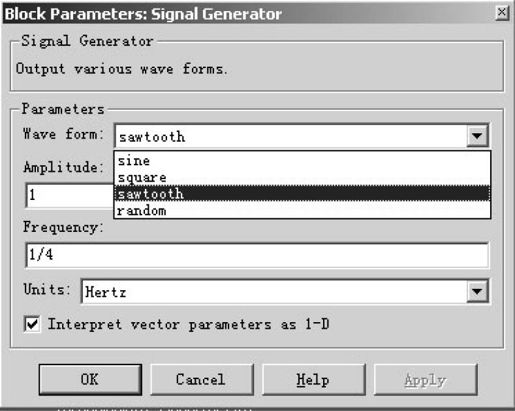
121-04

图5.14　信号发生器参数设置界面

模型连好后进行仿真，仿真结束后双击示波器，输出图形如图5.15所示。

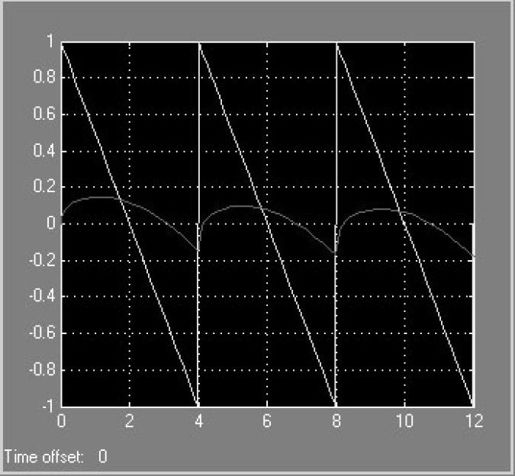
121-05

图5.15　例5-3输出曲线

【例5-4】　已知单位负反馈系统，其开环传递函数为G1(s)和G2(s)的串联，其中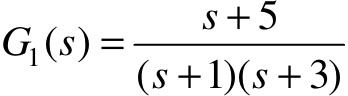 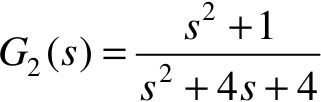121-5 ， 121-6 ，系统输入信号为r(t)=sin(t)，试用Simulink求取系统输出响应，并将输入和输出信号对比显示。

解：Simulink的模型如图5.16所示。

121-7

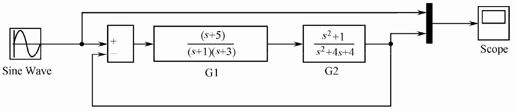
图5.16　例5-4的Simulink模型

Simulink中提供了用来建立系统模型的传递函数模块（Transfer Fcn）和零极点模块（Zero-Pole），可以方便地实现对系统的建模。本例中，G1(s)是用零极点表示的，选用“Zero-Pole”非常方便；G2(s)是用传递函数表示的，选用“Transfer Fcn”非常方便。信号源选择“Sine Wave”即可。

模型连好后进行仿真，仿真结束后，双击示波器，输出图形如图5.17所示。

122-01

图5.17　例5-4输出和输入曲线

5.3.2　时域响应性能指标求取

时域响应分析的是系统对输入和扰动在时域内的瞬态行为。系统特征，如上升时间、调节时间、超调量和稳态误差，均能从时域响应上反映出来。

利用MATLAB，不仅可以方便、快捷地计算系统的时域响应，绘制响应曲线，而且还能直接在响应曲线图上求取响应性能指标，或者通过简便的编程来求取。

5.3.2.1　游动鼠标法求取性能指标

在求取时域响应的程序运行完毕后，用鼠标左键单击时域响应曲线任意一点，系统会自动跳出一个小方框，小方框显示了这一点的横坐标（时间）和纵坐标（幅值）。按住鼠标左键在曲线上移动，可找到曲线幅值最大的一点，即曲线最大峰值，此时小方框显示的时间就是此二阶系统的峰值时间，根据观测到的稳态值和峰值可计算出系统的超调量。系统的上升时间和稳态响应时间可以此类推。

需要注意的是：由于显示精度和鼠标动作误差的原因，求取的性能指标可能与实际值有所误差，但这对分析问题是没有影响的。另外，游动鼠标法不适合用于plot()命令画出的图形，也就是说，它只能在用非plot函数输出的曲线上进行求取。

5.3.2.2　编程法求取性能指标

调用单位阶跃响应函数step()，可以获得系统的单位阶跃响应，当采用[y,t]=step(G)的调用格式时，将返回响应值y及相应的时间t，通过对y和t进行计算，可以得到时域性能指标。

峰值时间

峰值时间可由以下命令获得：

[Y,k]=max(y)          %求出y的峰值及相应的时间
timetopeak=t(k)       %获得峰值时间

应用取最大值函数max()求出y的峰值及相应的时间，并存于变量Y和k中。然后在变量t中取出峰值时间，并将它赋给变量timetopeak，它就是峰值时间。

超调量

超调量可由以下命令获得：

C=dcgain(G)         %求取系统的终值
[Y,k]=max(y)        %求出y的峰值及相应的时间
percentovershoot=100*(Y-C)/C     %计算超调量

dcgain()函数用于求取系统的终值，将终值赋给变量C，然后依据超调量的定义，由Y和C计算出百分比超调量。

上升时间

上升时间可利用MATLAB中的循环控制语句while编制M文件来获得，程序如下：

C=dcgain(G)        %求取系统的终值
n =1
while y(n)<C       %通过循环，求取输出第一次到达终值时的时间
n =n+1
end
risetime=t(n)      %获得上升时间

在阶跃输入条件下，y的值由零逐渐增大，当以上循环满足y=C时，退出循环，此时对应的时间即为上升时间。

对于输出无超调的系统响应，上升时间定义为输出从稳态值的10%上升到90%所需时间，则计算程序如下：

C=dcgain(G)        %求取系统的终值
n =1
while y(n)<0.1*C       %通过循环，求取输出第一次到达终值的10%时的时间
  n=n+1;
end
m=1;
while y(n)<0.9*C        %通过循环，求取输出第一次到终值的90%时的时间
m=m+1;
end
risetime=t(m)-t(n)       %上述两个时间相减，即为上升时间

调节时间

调节时间的计算程序如下：

C=dcgain(G)         %求取系统的终值
i =length(t)          %求取仿真时间t序列的长度
while(y(i)>0.98*C)&(y(i)<1.02*C)   %通过循环，求取输出在终值的±2%内的时间
  i =i-1
end
settlingtime=t(i)        %获得调节时间

【例5-5】　已知二阶系统传递函数为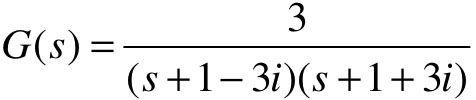 123-1 ，试分别用游动鼠标法和编程法求取系统的性能指标。

解：首先采用游动鼠标法来求取性能指标，在MATLAB工作空间中输入以下代码：

G=zpk([ ],[-1+3*i,-1-3*i],3);     %建立零极点模型
step(G);         %求取阶跃响应

运行程序后，输出阶跃响应曲线，利用游动鼠标法，可大致求出系统的性能指标，如图5.18所示。

124-2

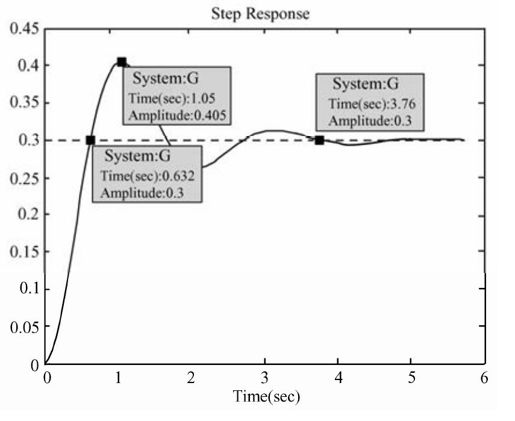
图5.18　例5-5的单位阶跃曲线

从图中可以看出，峰值时间为1.05 s；上升时间为0.632 s；超调为(0.405-0.3)/0.3×100%=35%；调节时间约为3.76 s。

下面采用编程法来求取性能指标，在MATLAB工作空间中输入以下代码：

G=zpk([ ],[-1+3*i,-1-3*i],3);     %建立零极点模型
        %计算最大峰值时间和它对应的超调量
    C=dcgain(G)
    [y,t]=step(G);                %求取阶跃响应
    plot(t,y)
    grid
    [Y,k]=max(y);
    timetopeak=t(k)               %取得最大峰值时间
    percentovershoot=100*(Y-C)/C  %计算超调量
    %计算上升时间
    n=1;
  while y(n)<C
    n=n+1;
  end
  risetime=t(n)
  %计算稳态响应时间
  i=length(t);
  while(y(i)>0.98*C)&(y(i)<1.02*C)
    i=i-1;
  end
  settlingtime=t(i)

运行后，输出结果为：

C = 0.3000
timetopeak =1.0491
    percentovershoot =35.0914
risetime =0.6626
settlingtime =3.5337

对比游动鼠标法的结果可知，峰值时间、上升时间、超调几乎完全相同，而调节时间的差距较大，那是因为游动鼠标时，找到稳态输出范围时有所误差，当然，这不会影响到问题的分析。

5.3.3　二阶系统参数对时域响应性能的影响

典型的二阶系统，其参数对系统的时域响应性能影响很大，深入了解这些参数与性能之间的影响关系，对于理解系统的特点、提出改善系统性能的方法都有很大的帮助。

通过MATLAB的计算与仿真，可以很直观地看出参数的变化对系统时域性能的影响。

5.3.3.1　闭环参数ωn和ζ的影响

从上文对性能指标的分析可知，tr，tp和ts均与ωn成反比，因此从对快速性的影响而言，ωn越大则响应越快。当然，ζ在一定程度上也对快速性有影响。

一般而言，ζ越小，快速性能越好，但由于ζ在实际中允许变化的范围是有限的，因此其对系统快速性的影响也是有限的。

另外，ζ唯一决定了σp%的大小，也就是说，ζ是决定系统相对稳定性的唯一因素，ζ越大，σp%越小。

【例5-6】　已知单位负反馈系统，其开环传递函数为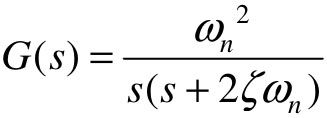 125-1 ，其中ωn=1，ζ为阻尼比，试绘制ζ分别为0, 0.2, 0.4, 0.6, 0.9, 1.2, 1.5时其单位负反馈系统的单位阶跃响应曲线绘制在同一张图上）。

解：MATLAB程序代码如下。

wn=1           %固有频率
sigma=[0, 0.2, 0.4, 0.6, 0.9, 1.2, 1.5]  %7个不同的阻尼比取值
num=wn*wn
t=linspace(0, 20, 200)'       %将t在0到20之间均等分成200份
for j=1:7
den=conv([1, 0], [1, 2*wn*sigma(j)]);    %求取开环传递函数的分母
s1=tf(num, den)              %建立开环传递函数
sys=feedback(s1, 1)          %建立单位负反馈系统的传递函数
y(:, j)=step(sys, t);        %求取单位阶跃响应
end
plot(t, y(:, 1:7)); grid     %在同一图上绘制单位阶跃响应曲线并添加栅格
title('典型二阶系统取不同阻尼比时的单位阶跃响应')  %添加图标题
%放置sigma取不同值的文字注释
gtext('sigma=0');  gtext('sigma=0.2');  gtext('sigma=0.4');  gtext('sigma=0.6');
gtext('sigma=0.9');  gtext('sigma=1.2');  gtext('sigma=1.5');

程序输出如图5.19所示。

126-1

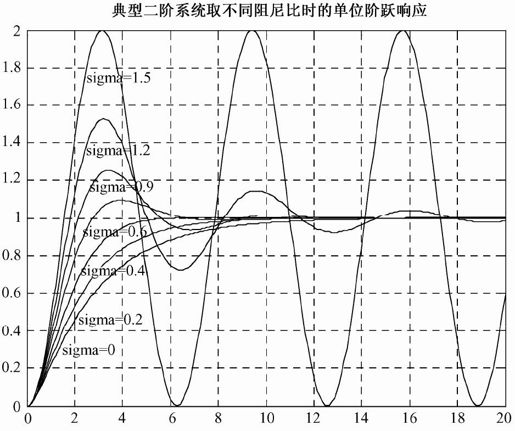
图5.19　例5-7输出结果

注意

上述程序中，gtext（'注释'）命令是使用鼠标放置的文字注释命令。当输入命令后，可以在屏幕上得到一个光标，单击鼠标后文字注释将放置在光标所指处。gtext常于同一个图上多条不同曲线的区别注释。

x=linspace(x1,x2,n)，创建了x1到x2之间有n个数据的数组，用来生成一组线性等距的数值，本书中常用linspace来等分时间。

从图5.19中可以明显看出，在ζ为0.4～0.9的范围内，系统上升较快，而超调又不太大，故在一般工程系统中，ζ就选在这个范围内，其中尤以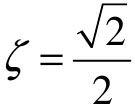 126-2 时响应较快，而此时σp%仅为4.3%，通常将此称为最佳阻尼，而具有最佳阻尼的二阶系统就称为二阶最佳系统。

5.3.3.2　开环参数K和T的影响

对一般的二阶系统而言，通过适当的变换，其闭环传递函数可用式（5-26）表示，其中K为回路增益，通常是可调节的，T为时间常数，通常由受控对象的特性决定，一般是不可以改变的。

126-3

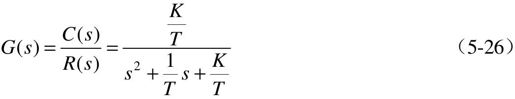
对比二阶系统的典型传递函数，可设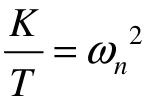 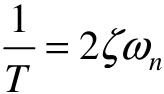126-4 ， 126-5 ，即

126-6

可见T越小，则ωn越大，ζ也越大，系统的快速性和相对稳定性同时转好。但在实际系统中，用T来改善系统性能的作用是有限的。

另一方面，K越大，则ωn越大，而ζ越小，表明K对快速性和相对稳定性的影响是矛盾的。在实际系统中，应根据系统的要求适当折中。

对二阶最佳系统而言，应有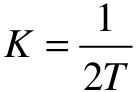 127-1 ，称之为二阶最佳参数关系。

【例5-7】　已知单位负反馈的二阶系统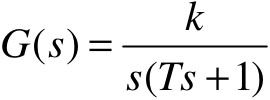 127-2 ，其开环传递函数，其中T=1，试绘制k分别为0.1, 0.2, 0.5, 0.8, 1.0, 2.4时，其单位负反馈系统的单位阶跃响应曲线（绘制在同一张图上）。

解：MATLAB程序代码如下。

T=1           %时间常数
k=[0.1, 0.2, 0.5, 0.8, 1.0, 2.4]    %6个不同的开环增益取值
t=linspace(0, 20, 200)'      %将t在0到20之间均等分成200份
num=1;  den=conv([1, 0], [T, 1])    %开环传递函数的分子、分母表达式
for j=1:6
s1=tf(num*k(j), den)       %建立开环传递函数
sys=feedback(s1, 1)        %建立单位负反馈系统的传递函数
y(:, j)=step(sys, t);      %求取单位阶跃响应
end
plot(t, y(:, 1:6));  grid     %在同一图上绘制单位阶跃响应曲线并添加栅格
title('典型二阶系统取不同开环增益时的单位阶跃响应')  %添加图标题
%放置k取不同值的文字注释
gtext('k=0.1'); gtext('k=0.2'); gtext('k=0.5'); gtext('k=0.8'); gtext('k=1.0'); gtext('k=2.4');

程序输出如图5.20所示。

127-3

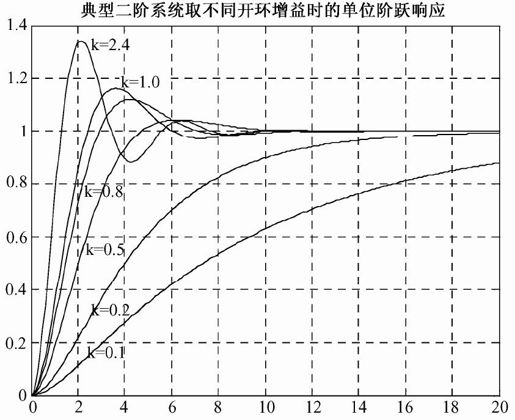
图5.20　例5-7输出结果

5.3.3.3　闭环极点分布对时域响应的影响

闭环极点分布对时域响应的影响可归结为以下几点：

（1）如果闭环极点落于虚轴上，则系统处于临界稳定状态；

（2）如果闭环极点是负实数极点，则系统阶跃响应是单调的，σp%=0；

（3）如果闭环极点是负实部的共轭复数极点，则系统阶跃响应是衰减振荡的，其超调量与初相角θ有关，θ角越大，则超调量越大；

（4）系统时域响应的快速性与闭环极点距虚轴的距离有关，距离越大，则ts越小；

（5）如果系统有多个闭环极点，则距虚轴越近的闭环极点所起的作用越大，如果一个闭环极点距虚轴的距离较另一个闭环极点距虚轴的距离大5倍或5倍以上，则距离远的闭环极点的影响可以忽略不计。

5.3.4　改善系统时域响应性能的一些措施

如前文所述，想单纯通过改变回路增益K来达到系统时域响应又快又稳是不可能的，只能做一个合理的折中。下面给出两种可以提高系统性能的方法。

5.3.4.1　输出微分反馈

在基本系统的基础上，从输出向输入端引入附加的微分负反馈控制，如图5.21所示。

128-1

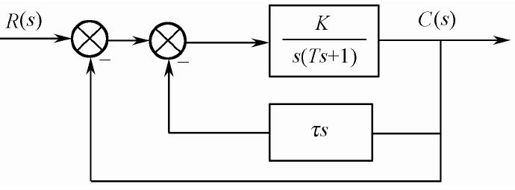
图5.21　带输出微分反馈的二阶系统

可按K、T与ωn、ζ的关系，将原开环传递函数改写为：

128-2

式中，ωn和ζ是τ=0时原系统的固有频率和阻尼系数。当τ不等于0时，由其闭环传递函数可推出：

128-3

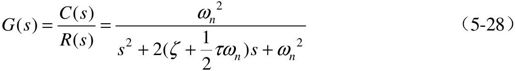
显然，加微分反馈后，系统的固有频率ωn不变，而阻尼比提高。

128-4

由于输出微分反馈可以在不改变快速性的条件下提高相对稳定性，因此实际中可通过提高K来进一步提高快速性，而用τ来保证必要的相对稳定性，即采用输出反馈，这样既可以提高系统的相对稳定性，又可以提高其快速性。

【例5-8】　已知单位负反馈的二阶系统，其中T=1，K=1，试绘制τ分别为0, 0.05, 0.2, 0.5, 1.0, 2.4时，其单位负反馈系统的单位阶跃响应曲线（绘制在同一张图上）。

解：MATLAB程序代码如下。

T=1          %时间常数
k=1          %开环增益k的值
tou=[0, 0.05, 0.2, 0.5, 1.0, 2.4]   %6个不同的微分反馈系数
t=linspace(0, 20, 200)'             %将t在0到20之间均等分成200份
num=1        %开环传递函数的分子表达式
for j=1:6
den=conv([1, 0], [T, 1+tou(j)])     %求取开环传递函数的分母表达式
s1=tf(num*k, den)          %建立开环传递函数
sys=feedback(s1, 1)        %建立单位负反馈系统的传递函数
y(:, j)=step(sys, t);      %求取单位阶跃响应
end
plot(t, y(:, 1:6));  grid      %在同一图上绘制单位阶跃响应曲线并添加栅格
title('典型二阶系统采用输出微分反馈时的单位阶跃响应')    %添加图标题
%放置k取不同值的文字注释
gtext('tou=0'); gtext('tou=0.05'); gtext('tou=0.2'); gtext('tou=0.5'); gtext('tou=1.0'); gtext('tou=2.4');

程序输出如图5.22所示。

129-1

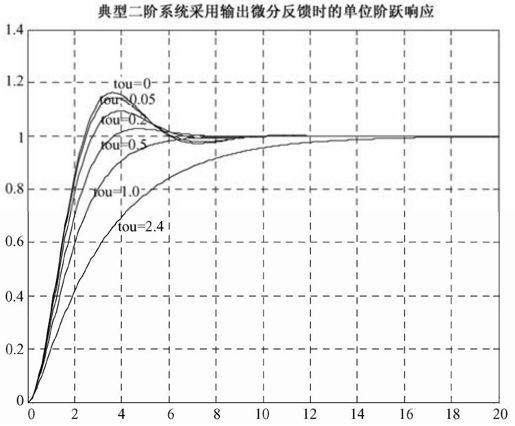
图5.22　例5-8输出结果

5.3.4.2　比例微分控制

在基本系统的基础上，在前向通道中增加微分控制就构成了带比例微分控制的二阶系统，如图5.23所示。

129-3

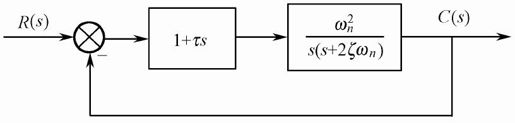
图5.23　带比例微分控制的二阶系统

其闭环传递函数为：

129-2

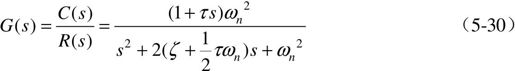
由此可知，比例微分控制同样能实现在不改变ωn的条件下提高系统阻尼比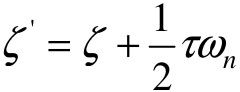 130-1 的效果，作用类似输出微分反馈控制。但与输出微分反馈控制不同的是，在闭环传递函数中增加了一个零点 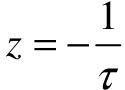130-2 ，分析表明，它的存在将使系统的上升加快，但σp%会有所增加，其趋势随τ的加大而加大。

【例5-9】　设系统闭环传递函数为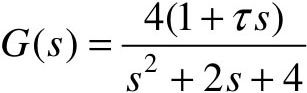 130-3 ，试求取τ=0, 0.2, 0.4时的单位阶跃响应（绘制在同一张图上）。

解：MATLAB程序代码如下。

tou=[0, 0.2, 0.4]              %3个不同的微分时间常数
t=linspace(0, 8, 80)'          %将t在0到8之间均等分成80份
num=4 ;  den=[1, 2, 4]         %开环传递函数的分子、分母表达式
for j=1:3
sys=tf( conv(num, [tou(j), 1]), den)    %建立系统传递函数
y(:, j)=step(sys, t);          %求取单位阶跃响应
end
plot(t, y(:, 1:3)); grid;      %将3条响应曲线绘制在同一个图上并添加栅格
title('比例微分控制，不同微分时间下的系统阶跃响应')   %添加图标题
gtext('tou=0');  gtext('tou=0.2');  gtext('tou=0.4'); %放置tou取不同值的文字注释

程序输出如图5.24所示。

130-4

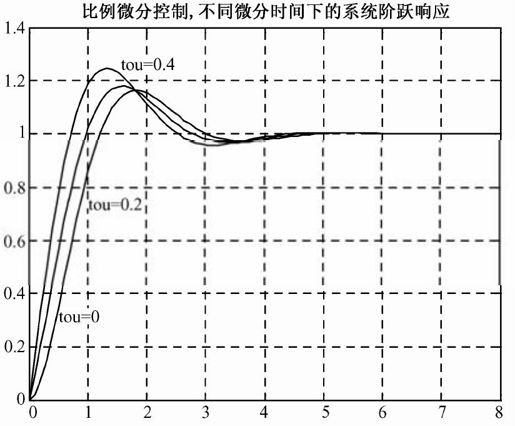
图5.24　例5-9输出结果

从图5.24可以看出，随着微分时间常数τ的增大，系统的上升加快，σp%也随之增大。

【例5-10】设系统的传递函数为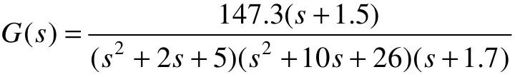 130-5 ，试分析其主导极点，并比较由主导极点构成的系统与原系统的单位阶跃响应。

解：系统有5个极点：p1,2=-5±i，p3,4=-1±2i，p5=-1.7和一个零点z1=-1.5。显然，主导极点为p3,4=-1±2i，由主导极点构成的系统传递函数为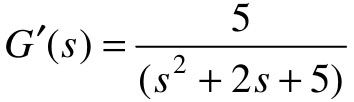 131-1 。值得注意的是，两个传递函数的静态增益应该相同。

计算阶跃响应的MATLAB代码如下：

k=147.3           %原系统的增益
t=0:0.1:6         %仿真时间
num0=k*[1, 1.5]
den00=[1, 2, 5]; den01=[1, 10, 26]; den02=[1, 1.7]  %传递函数分母的系数
sys0=tf(num0, conv(den00, conv(den01, den02) ) )    %建立原系统传递函数
y0=step(sys0, t)       %求取原系统的阶跃响应
num1=5
sys1=tf(num1, den00)   %建立主导极点所构成的系统传递函数
y1=step(sys1, t)       %求取主导极点所构成的系统的阶跃响应
plot(t, y0, t, y1); grid    %绘制阶跃响应曲线并添加栅格
title('阶跃响应对比')         %添加图标题
%放置区别两条曲线的文字注释
gtext('原系统的单位阶跃响应'); gtext('主导极点构成的系统的单位阶跃响应')

输出结果如图5.25所示。

131-2

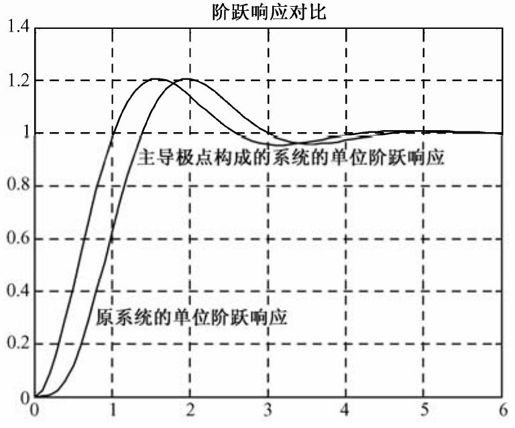
图5.25　例5-10输出结果

从图5.25可以看出，主导极点构成的系统和原系统在动态性能上差别很小。

【例5-11】　设系统的闭环传递函数G(s)为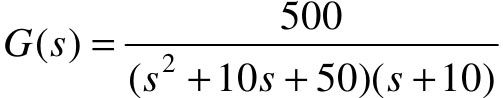 131-3 ，试分析其主导极点，并比较由主导极点构成的系统与原系统的单位阶跃响应。

解：系统有3个极点p1,2=-5±5i，p3=-10。显然，主导极点为p1,2=-5±5i，由主导极点构成的系统传递函数为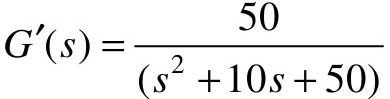 131-4 ，值得注意的是，两个传递函数的静态增益应该相同。

Simulink的模型如图5.26所示。图中“Transfer Fcn”建立主导极点构成系统的部分，“Transfer Fcn1”建立非主导极点构成系统的部分，这两部分串联。

132-1

图5.26　例5-11的Simulink模型

模型连好后，进行仿真，仿真结束后，双击示波器，输出图形如图5.27所示。

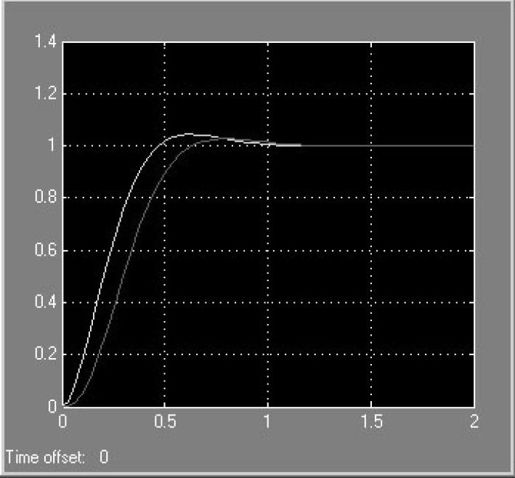
132-03

图5.27　例5-11输出结果

从图5.27可以看出，主导极点构成的系统和原系统在动态性能上差别很小。

5.3.5　LTI Viewer应用

除了采用Simulink和编写程序的方法之外，MATLAB控制系统工具箱还为线性时不变系统的分析提供了一个图形用户界面LTI Viewer（Linear-Time-Invariant Viewer），可以非常直观、简捷地分析控制系统的时域、频域响应。

LTI Viewer让使用者可在图形化界面中同时通过图表得知一个或数个系统的变化，也就是说使用

者可在图形化界面中分析系统的时域和频域特性，例如，时域分析方面的阶跃响应、冲激响应、极点、零点以及频域分析方面的Bode图、Nyquist图、Nichols图和奇异点图等。而且，LTI Viewer还可展现、标示出重要的响应状况，包括稳定边界、峰值和调节时间等。

LTI Viewer的功能强大，应用广泛。出于篇幅的考虑，本书只对其基本功能进行简要介绍，其他功能的使用和操作与基本功能大同小异，读者可触类旁通。

同时，LTI Viewer是图形用户界面，交互性好，直观，非常容易掌握和熟练。

LTI Viewer的使用非常简单，只需要以下两步简单的操作：

（1）在MATLAB工作空间中建立好控制系统的数学模型；

（2）在命令窗口中输入“LTI View”，调出LTI View窗口，便可对控制系统进行许多功能的分析。

下面以控制系统的模型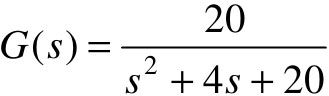 132-2 为例进行介绍

【步骤1】　建立数学模型。

使用LTI Viewer，首先需要建立一个MATLAB工作空间中的模型或M文件，然后导入到LTI Viewer中。本例中，在MATLAB工作空间中建立数学模型，在MATLAB命令窗口输入以下代码：

num = [0 20];  den = [1 4 20];   %传递函数分子、分母多项式系数
sys = tf(num,den)                %建立传递函数模型

这便在MATLAB工作空间中建立了G(s)的数学模型，后面将采用LTI Viewer对其进行相应的分析。

【步骤2】　进入LTI View窗口。

在命令窗口中输入“lti view”，即可进入可视化仿真环境，如图5.28所示。

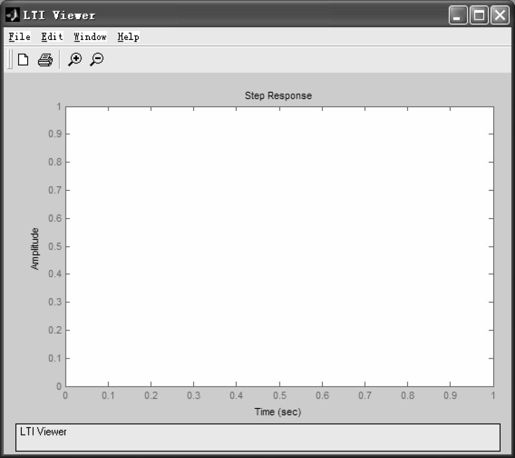
133-01

图5.28　LTI Viewer主界面

【步骤3】　在LTI Viewer中导入控制系统的模型。

进入LTI Viewer后，单击【File】，选择【Import】选项，将弹出如图5.29所示的窗口。该窗口显示了当前工作空间或指定工作目录内所有的系统模型对象。

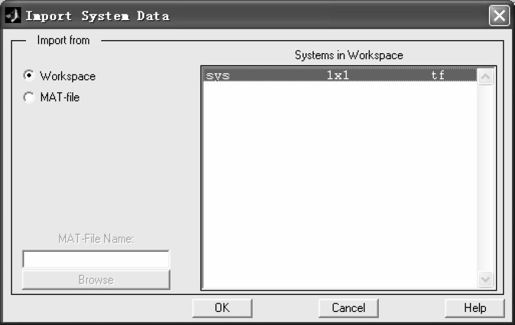
133-02

图5.29　LTI Viewer的Import选项窗口

选择需要分析的模型，将模型导入到LTI Viewer中。选中刚刚在工作空间中建立好的闭环系统数学模型对象sys，单击“OK”按钮。此时，LTI Viewer会自动绘制出系统的阶跃响应曲线，如图5.30所示。

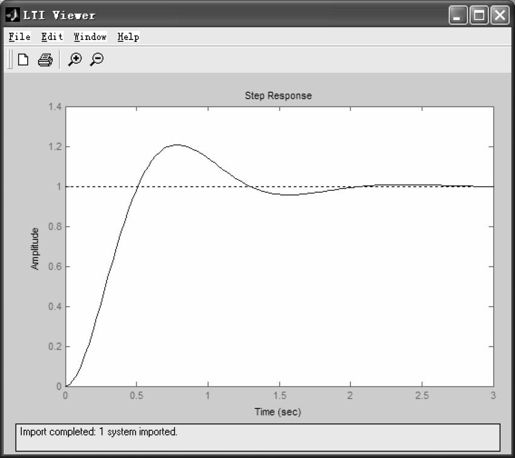
134-01

图5.30　LTI Viewer绘制出的系统的阶跃响应曲线

【步骤4】　操作功能丰富的现场菜单。

在上述阶跃响应曲线窗口内单击鼠标右键，弹出现场菜单，如图5.31所示。从图5.31中可以看出，现场菜单具有丰富的控制系统分析的功能，菜单的主要功能如下。

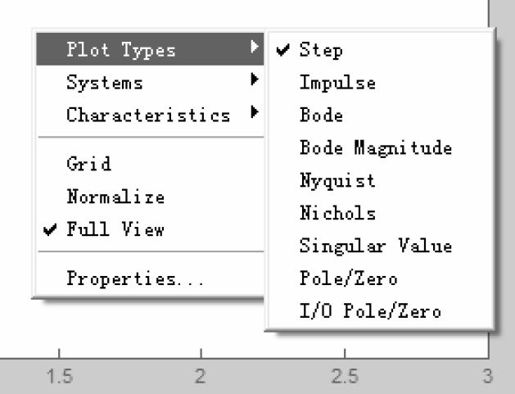
134-02

图5.31　LTI Viewer提供的现场菜单

Plot Types：选择图形类型。

可选择Step（阶跃响应，默认设置）、Impulse（脉冲响应）、Bode图、Bode Magnitude（幅频Bode图）、Nyquist图、Nichols图、Singular Value（奇异点图）和Pole/Zero（极点/零点图）等。

Characteristics：可对不同类型响应曲线标出相关特征值。

例如，对阶跃响应，可选择表示的系统特征的上升时间、调节时间、超调等。

Properties：对图形窗口进行编辑，对显示性能参数进行设置。

此外，还可以通过菜单Edit→Linestyle对曲线的线形、颜色、标志等进行选择。

本例中，在菜单中选择不同的绘图方式就会在LTI Viewer的主窗口中立即得到相应的曲线。比如，选择冲激响应Impulse，结果如图5.32所示。

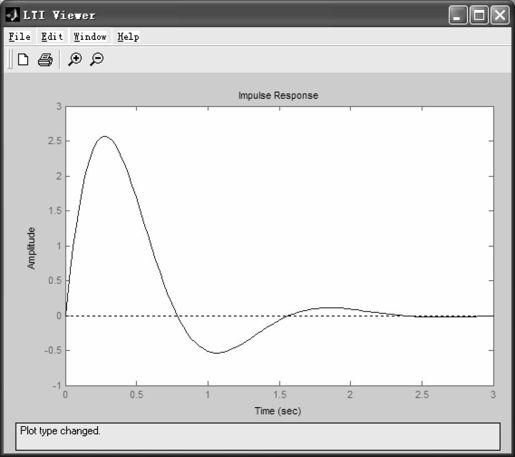
134-03

图5.32　LTI Viewer绘制的系统冲激响应曲线

【步骤5】　配置图形窗口，实现多图形窗口显示。

LTI Viewer还支持同时显示多条曲线的功能。选择菜单【Edit】→【Plot Configurations】后，弹出图形配置窗口。该窗口左边显示响应图的6种排列形式，通过单选按钮任选其中一种，最多有6种图形显示。该窗口右边显示响应类型，共6组，最多可选择6种（应和所选窗口数对应），如图5.33所示。

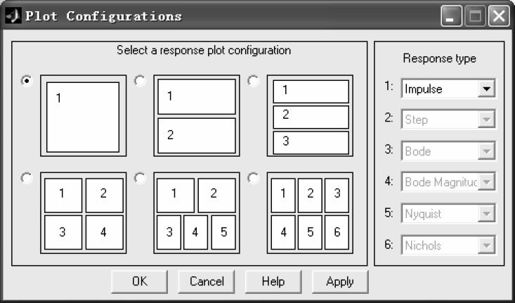
135-01

图5.33　LTI Viewer的配置图形窗口

选择合适的图形显示方式，并且分别指定每个子窗口的曲线类型，就可以分析系统各个方面的特性。本例中，设定LTI Viewer同时显示4幅图像，分别为系统的阶跃响应曲线、冲激响应曲线、幅频特性曲线以及Nyquist曲线，结果如图5.34所示。

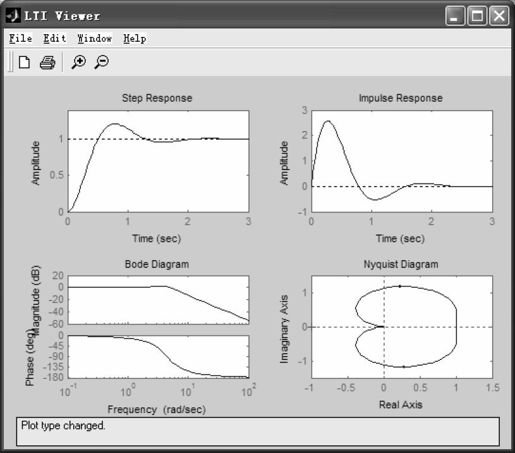
135-02

图5.34　LTI Viewer同时显示4条曲线

对图5.34中的每条曲线，还可以分别设置相关的选项。比如，可以在阶跃响应曲线中设置显示峰值、稳定时间、上升时间及系统稳态等参数，如图5.35所示。

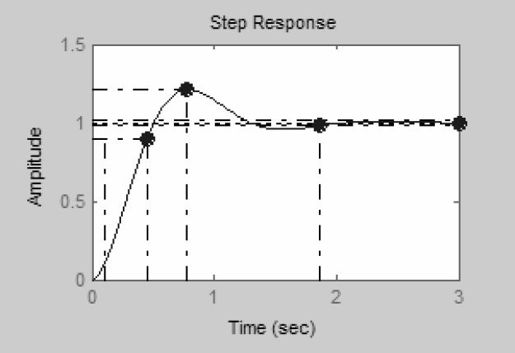
135-03

图5.35　系统阶跃响应的主要参数

读者可以尝试利用该工具分析线性时不变系统。MATLAB中还有大量类似的工具，不仅大大减少了用户的编程代码量，还提供了非常直观、简捷的人机交互界面，提高了工作的效率。

5.3 MATLAB/Simulink在时域分析中的应用