13.4　MATLAB/Simulink在线性二次型最优控制中的应用

在MATLAB中，有专门求解连续系统线性二次型最优控制问题的函数lqr()、lqr2()及lqry()，常见的调用格式为：

[K,P,E] = lqr(A,B,Q,R,N)
[K,P,E] = lqr2(A,B,Q,R,N)
[K,P,E] = lqry(sys,Q,R,N)

其中，输入的参数中，A为系统的状态转移矩阵，B为输入矩阵，Q为给定的半正定矩阵，R为给定的正的实对称矩阵，N为性能指标中交叉乘积项的加权系数矩阵。

返回的参数中，K表示最优反馈矩阵，P是Riccati方程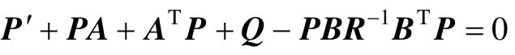的解，E则是A-BK的特征值。

lqr2与lqr在调用上是完全相同的，只是使用的算法不同。lqry用于求解二次型状态调节器的特例，采用输出反馈代替状态反馈。此时，最优控制为

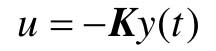
性能指标则转化为

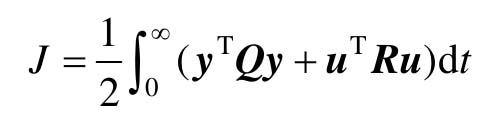
也被称为次优控制。

对于离散系统线性二次型最优控制问题，MATLAB提供了完全相似的函数dlqr和dlqry，常见的调用格式为

[K,P,E] = dlqr(A,B,Q,R,N)
[K,P,E] = dlqry(A,B,C,D,Q,R,N)

输入、输出中各参数的含义同前。