4.3　拉氏变换与控制系统模型

动态系统数学模型有多种表达形式，可以是微分方程、差分方程，也可以是传递函数、状态方程。微分方程描述的系统模型，通过求解微分方程，可以得到系统随时间变化的规律，比较直观。但是，当微分方程阶次较高时，微分方程的求解变得十分困难，不易实现，而采用拉氏变换就能把问题的求解从原来的时域变换到复频域，把微分方程变成代数方程，而代数方程的求解通常是比较简单的，求解代数方程后，再通过拉氏反变换得到微分方程的解，两者的关系及运算过程如图4.5所示。

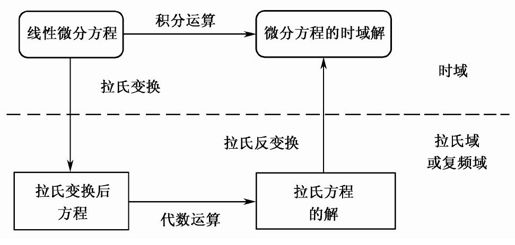
图4.5　拉氏变换和拉氏反变换

时域函数f(t)的拉氏变换定义如下：

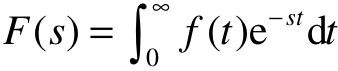
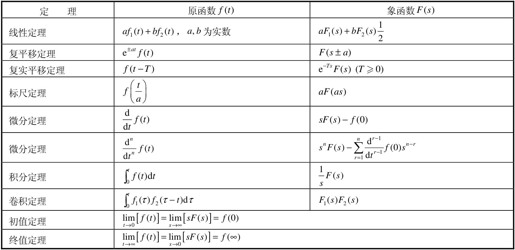
用符号表示为F(s)=￡[f(t)]，s称为拉氏算子，它的单位是1/时间，即频率。由于s是复数，因此它还表示复频域变量。拉氏变换的基本定理见表4.1，常用函数的拉氏变换见表4.2。

表4.1　拉氏变换的基本定理

时域函数经过拉氏变换后得到拉氏函数，拉氏反变换定义为：

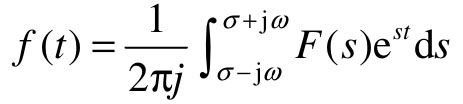
用符号表示为f(t)=￡-1[F(s)]。

直接对F(s)积分来计算f(t)是复杂的，通常可通过拉氏变换表查找。

表4.2　常用函数的拉氏变换

【例4-3】　求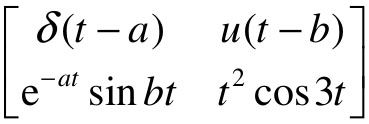的拉氏变换。

解：MATLAB程序代码如下。

syms t s;           %定义符号变量
syms a b positive         %定义符号变量
Dt=sym('Dirac(t-a)');    %冲激函数delta(t-a)用Maple函数库中的定义是Dirca(t-a)
Ut=sym('Heaviside(t-b)'); %单位阶跃函数u(t-b)用Maple函数库中的定义是Heaviside(t-b)
Mt=[Dt, Ut;exp(-a*t)*sin(b*t), t^2*exp(-t)];    %建立矩阵
MS=laplace(Mt, t, s)         %进行拉氏变换

程序运行后，输出的结果为：

MS = [ exp(-a*s),           exp(-b*s)/s]
         [ b/((s+a)^2+b^2),       2/(1+s)^3]