7.7　频率法的稳定性分析

7.7.1　Nyquist稳定判据

Nyquist稳定判据是由H.Nyquist于1932年提出的。它利用开环系统幅相频率特性（Nyquist图）来判断闭环系统的稳定性。Nyquist稳定判据的理论基础是复变函数理论中的幅角定理，也称映射定理。

为将映射定理与控制系统稳定性分析联系起来，适当选择S平面的封闭曲线Cs，如图7.14所示。它由整个虚轴和半径为∞的右半圆组成，试验点按顺时针方向移动一圈，得到的封闭曲线称为Nyquist轨迹。

193-1

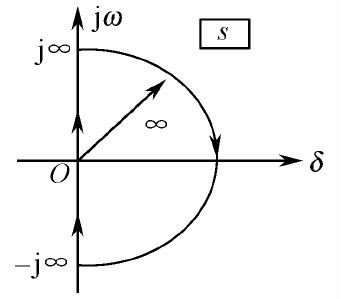
图7.14　S平面上的Nyquist轨迹

Nyquist轨迹在F(s)平面上的映射也是一条封闭曲线，称为Nyquist曲线。

Nyquist轨迹Cs由两部分组成，一部分沿虚轴由下而上移动，试验点s=jω在整个虚轴上的移动，其在F平面上的映射就是曲线F(jω)（ω由-∞→+∞），如图7.15所示。

193-2

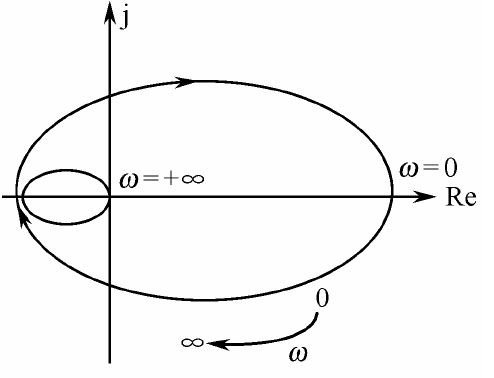
图7.15　F平面上的Nyquist曲线

曲线也可用式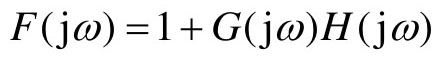193-3表示。Nyquist轨迹Cs的另一部分为S平面上半径为∞的右半圆，映射到F平面上为：193-4。

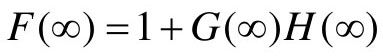根据映射定理可得，S平面上的Nyquist轨迹在F平面上的映射F(jω)（ω由-∞→+∞）逆时针包围坐标原点的次数N为：

193-5

式中，Z表示位于右半平面F(s)=1+G(s)H(s)的零点数，即闭环右极点个数；P表示位于右半平面F(s)=1+G(s)H(s)的极点数，即开环右极点个数；N表示Nyquist曲线包围坐标原点的次数。

闭环系统稳定的条件为系统的闭环极点均在S平面的左半平面，即Z=0或N=P。

  1. Nyquist稳定判据一

当系统开环传递函数G(s)H(s)在s平面的原点及虚轴上无极点时，Nyquist稳定判据可表示为：当ω从-∞→+∞变化时的Nyquist曲线G(jω)H(jω)逆时针包围（-1, j0）点的次数N等于系统G(s)H(s)位于右半S平面的极点数P时，即当N=p时，闭环系统稳定，否则闭环系统不稳定（N≠P）。

由Nyquist曲线G(jω)H(jω)（ω从0→+∞）判别闭环系统稳定性的Nyquist判据为：G(jω)H(jω)曲线（ω为0→+∞）逆时针包围(-1, j0)的次数为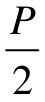194-1。

  1. Nyquist稳定判据二

设系统开环传递函数为：

194-2

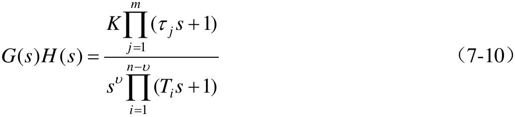
式中，v表示开环传递函数中位于原点的极点个数。

Nyquist轨迹的修正如图7.16所示。

194-3

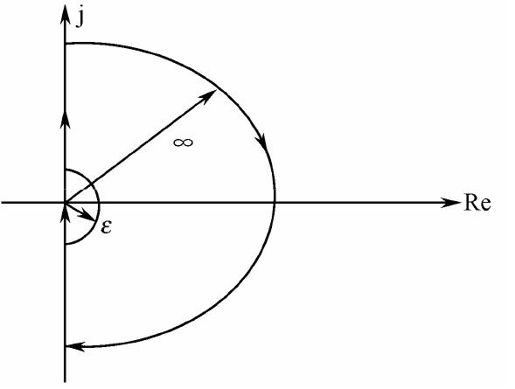
图7.16　绕过原点的Nyquist轨迹

Nyquist轨迹由4部分组成：

  • 以原点为圆心，以无限大为半径的大半圆；
  • 由-j∞到j0-的负虚轴；
  • 由j0+沿正虚轴到+j∞；
  • 以原点为圆心，以ε(ε→0)为半径的从j0-到j0+的小半圆。

考虑S平面上有位于坐标原点的v个极点，Nyquist曲线稳定判据为：当系统开环传递函数有v个极点位于S平面坐标原点时，如果增补开环频率特性曲线G(jω)H(jω)（ω从-∞→+∞）逆时针包围（-1, j0）点的次数N等于系统开环右极点个数P，则闭环系统稳定，否则系统不稳定。

Nyquist对数稳定判据是对数幅相频率特性的稳定判据，实际上是Nyquist稳定判据的另一种形式，即利用开环系统的对数频率特性曲线（Bode图）来判别闭环系统的稳定性，而Bode图又可通过试验获得，因此在工程上获得了广泛的应用。

Nyquist图与Bode图的对应关系如图7.17所示。

194-4

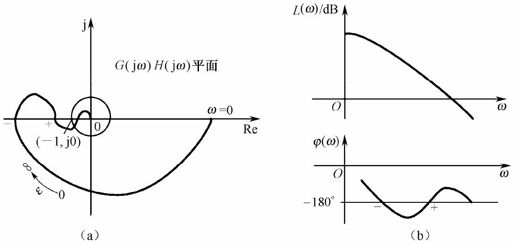
图7.17　Nyquist图和Bode图的对应关系

采用对数频率特性曲线（Bode图）时，Nyquist稳定判据可表述为：当ω由-∞→+∞变化时，在开环对数幅频特性曲线L(ω)≥0的频段内，相频特性曲线对-180°线的正穿越与负穿越次数之差为P（P为S平面右半平面开环极点数），则闭环系统稳定。

7.7.2　稳定裕度

  1. 相对稳定性

从Nyquist稳定判据可知，若系统开环传递函数没有右半平面的极点且闭环系统是稳定的，则开环系统的Nyquist曲线离（-1, j0）点越远，闭环系统的稳定性越好；开环系统的Nyquist曲线离（-1, j0）点越近，闭环系统的稳定性越差，这就是通常所说的控制系统相对稳定性。

系统的相对稳定性用Nyquist曲线相对点（-1, j0）的靠近程度来度量，定量表示为增益裕度和相角裕度。

  1. 增益裕度

增益裕度用于表示G(jω)H(jω)曲线在负实轴上相对于（-1, j0）点的靠近程度。

当G(jω)H(jω)曲线与负实轴交于G点时，G点的频率ωg称为相位穿越频率，此时ωg处的相角为-180°，幅值为|G(jω)H(jω)|，开环频率特性幅值|G(jω)H(jω)|的倒数称为增益裕度（或幅值裕度），用Kg表示：

195-2

式中，ωg满足195-3。

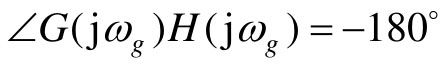图7.18中的ωg在Bode图中对应于相频特性上相角为-180°的频率，如图7.19所示。

195-4

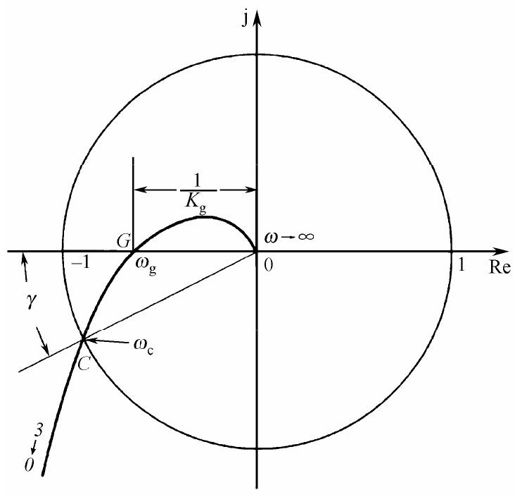
图7.18　最小相位系统的Nyquist图

195-5

图7.19　对数频率特性

增益裕度用分贝数表示为：

195-6

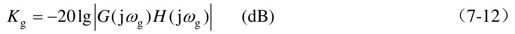
对于最小相位系统：

  • 当|G(jωg)H(jωg)|<1或201g|G(jωg)H(jωg)|<0时，闭环系统稳定；
  • 当|G(jωg)H(jωg)|>1或201g|G(jωg)H(jωg)|>0时，闭环系统不稳定；
  • 当|G(jωg)H(jωg)|=1或201g|G(jωg)H(jωg)|=0时，系统处于临界状态。

临界状态下的开环系统不稳定。为使临界状态下的闭环系统稳定，G(jω)H(jω)曲线应包围（-1, j0）点，此时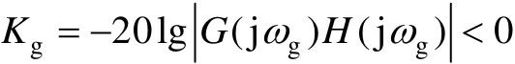196-1，闭环系统稳定。

因此，增益裕度Kg表示系统处于临界状态时，系统增益所允许的增大倍数。

  1. 相角裕度

为了表示系统相角变化对系统稳定性的影响，引入相角裕度的概念。

ωc称为穿越频率，也称剪切频率或截止频率，在图7.16中，G(jω)H(jω)与单位圆相交于C点，C点处的频率为ωc，此时|G(jω)H(jω)|=1。

使系统达到临界稳定状态而尚可增加的滞后相角就称为系统的相角裕度或相角裕度，表示为：

196-2

相角裕度γ是增益穿越频率ωc处相角与-180°线之间的距离。

对于最小相位系统：

  • 当γ>0时，闭环系统稳定；
  • 当γ<0时，闭环系统不稳定。

增益裕度和相角裕度通常作为设计和分析控制系统的频域指标，但仅用其中之一是不足以说明系统相对稳定性的。

  1. 用幅相频率特性曲线分析系统稳定性

若采用幅相频率特性曲线，如果当G(jω)H(jω)的开环增益发生变化时，曲线仅是上下简单平移，而当对G(jω)H(jω)增加一个恒定相角时，曲线为水平平移，那么这对分析系统稳定性与系统参数之间的相互影响是非常有利的。

7.7.3　MATLAB在稳定性分析中的应用

MATLAB提供了用于计算系统稳定裕度的函数margin，其调用法则如下。

margin函数可以从频率响应数据中计算出幅值裕度、相角裕度以及对应的频率。幅值裕度和相角裕度是针对开环SISO系统而言的，它指出了系统在闭环时的相对稳定性。当不带输出变量引用时，margin可在当前图形窗口中绘出带有裕量及相应频率显示的Bode图，其中的幅值裕度以分贝为单位。

幅值裕度是在相角为-180°处使开环增益为1的增益量，如在-180°相频处的开环增益为g，则幅值裕度为1/g；若用分贝值表示幅值裕度，则为-20lg10g。类似地，相角裕度是当开环增益为1.0时，相应的相角与180°角的和。

margin(mag, phase, w)：由bode指令得到的幅值mag（不是以dB为单位）、相角phase及角频率w矢量绘出带有裕量及相应频率显示的Bode图。

margin(num, den)：计算连续系统传递函数表示的幅值裕度和相角裕度，并绘出相应的Bode图。类似地，margin(a, b, c, d)可计算出连续状态空间系统表示的幅值裕度和相角裕度，并绘出相应的Bode图。

[gm, pm, wcg, wcp]=margin(mag, phase, w)：由幅值mag（不是以dB为单位）、相角phase及角频率w矢量计算系统幅值裕度和相角裕度及相应的相角交界频率wcg、截止频率wcp，而不直接绘出Bode图。

MATLAB 6.0以上版本还提供了计算系统稳定裕度的函数allmargin，其调用法则如下。

s=allmargin(sys)：计算幅值裕度、相角裕度以及对应的频率。幅值裕度和相角裕度是针对开环SISO系统而言，输出s是一个结构体，它包括幅值裕度、相角裕度以及对应的频率、时滞增益裕度。

【例7-5】　已知一高阶系统的开环传递函数为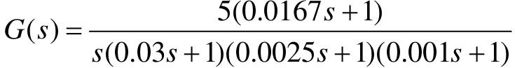197-1，试计算系统的相角稳定裕量和幅值稳定裕量，并绘制系统的Bode图。

解：MATLAB程序代码如下。

  1. num=5*[0.0167, 1]       %传递函数分子多项式系数行向量
  2. den=conv( conv([1, 0], [0.03, 1]), conv([0.0025, 1], [0.001, 1]))
  3.                         %分母多项式系数行向量
  4. G=tf(num, den)          %建立传递函数
  5. w=logspace(0, 4, 50)    % w为100～104之间对数等间距分布的50个数
  6. bode(G, w) ; grid;      %绘制Bode图并添加栅格
  7. [Gm, Pm, Wcg, Wcp]=margin(G)    %求稳定裕量所示。

运行程序，输出曲线如图7.20所示。

197-2

图7.20　例7-5系统的Bode图

运行结果如下：

  1. Gm = 455.2548
  2. Pm = 85.2751
  3. Wcg = 602.4232
  4. Wcp = 4.9620

由运行结果可知，幅值稳定裕量Kg=455.2548；相角稳定裕量γ=85.2751°；相角穿越频率ωg=602.4232 rad/s；幅值穿越频率（截止频率）ωc=4.9620 rad/s。

【例7-6】　已知一高阶系统的开环传递函数为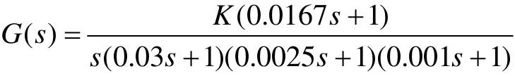197-3，试计算当开环增益K=5、500、8003 000时，系统稳定裕量的变化。

解：MATLAB程序代码如下。

  1. k=[5, 500, 800, 3000]     %不同的开环增益
  2. for j=1:4
  3. num=k(j)*[0.0167, 1]     %传递函数分子多项式系数行向量
  4. den=conv( conv([1, 0], [0.03, 1]), conv([0.0025, 1], [0.001, 1]))
  5.                          %分母多项式系数行向量
  6. G=tf(num, den)           %建立传递函数
  7. y(j)=allmargin(G)        %计算幅值裕度、相角裕度以及对应的频率
  8. end
  9. y(1);  y(2) ;  y(3) ;  y(4) ;

运行结果如下：

  1. %y(1)，开环增益K=1时，系统的幅值裕度、相角裕度以及对应的频率
  2. ans =   GMFrequency: 602.4232
  3.         GainMargin: 455.2548
  4.         PMFrequency: 4.9620
  5.         PhaseMargin: 85.2751
  6.         DMFrequency: 4.9620
  7.         DelayMargin: 0.2999
  8.         Stable: 1
  9. %y(2)，开环增益K=500时，系统的幅值裕度、相角裕度以及对应的频率
  10. ans =   GMFrequency: 602.4232
  11.         GainMargin: 4.5525
  12.         PMFrequency: 237.7216
  13.         PhaseMargin: 39.7483
  14.         DMFrequency: 237.7216
  15.         DelayMargin: 0.0029
  16.         Stable: 1
  17. %y(3)，开环增益K=800时，系统的幅值裕度、相角裕度以及对应的频率
  18. ans =   GMFrequency: 602.4232
  19.         GainMargin: 2.8453
  20.         PMFrequency: 329.9063
  21.         PhaseMargin: 27.7092
  22.         DMFrequency: 329.9063
  23.         DelayMargin: 0.0015
  24.         Stable: 1
  25. %y(4)，开环增益K=3000时，系统的幅值裕度、相角裕度以及对应的频率
  26. ans =   GMFrequency: 602.4232
  27.         GainMargin: 0.7588
  28.         PMFrequency: 690.5172
  29.         PhaseMargin: -6.7355
  30.         DMFrequency: 690.5172
  31.         DelayMargin: 0.0089
  32.         stable: 0

由运行结果可知，随着开环增益的增大，相角稳定裕度在减小，表明系统的稳定性在变差。当K=3 000时，相角稳定裕度变为负值，此时系统不稳定了。

【例7-7】　已知系统的开环传递函数为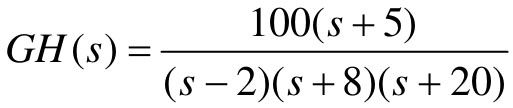199-1，试绘制系统的极坐标图，并利用Nyquist稳定判据判断闭环系统的稳定性。

解：MATLAB程序代码如下。

  1. k=100;  z=[-5];  p=[2, -8, -20]       %开环传递函数的零极点和增益
  2. G=zpk(z, p, k)                        %建立传递函数
  3. nyquist(G) ; grid                     %绘制Nyquist图并添加栅格

运行结果如图7.21所示。

199-2

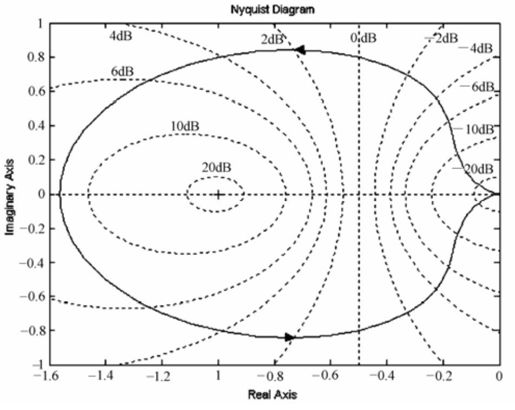
图7.21　例7-7开环系统的Nyquist图

从图7.21可以看出，开环系统有一个S右半平面的极点（p=1），因此开环系统是不稳定的。开环系统的Nyquist图逆时针包围（-1, j0）点1次，那么根据Nyquist稳定判据可知，闭环系统是稳定的。

【例7-8】　已知系统的开环传递函数为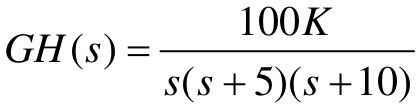199-3，试分别绘制K=1, 7.8, 20时系统的极坐标图，并利用Nyquist稳定判据判断闭环系统的稳定性。

解：MATLAB程序代码如下。

  1. z=[];  p=[0, -5, -10];  k=100.*[1, 7.8, 20]     %开环传递函数的零极点和增益
  2. G=zpk(z, p, k(1)) ;  [re1, im1]=nyquist(G)      %建立传递函数，绘制Nyquist图
  3. G=zpk(z, p, k(2));  [re2, im2]=nyquist(G)       %建立传递函数，绘制Nyquist图
  4. G=zpk(z, p, k(3));  [re3, im3]=nyquist(G)       %建立传递函数，绘制Nyquist图
  5. plot( re1(:), im1(:), re2(:), im2(:), re3(:), im3(:))   %
  6. v=[-5, 1, -5, 1];  axis(v)
  7. grid                                            %添加栅格
  8. xlabel('Real Axis'); ylabel('Imaginary Axis');  %标注坐标轴
  9. text(-0.4, -3.6, 'K=1');  text(-2.7, -2.7, 'K=7.8');  text(-4.4, -1.6, 'K=20'
  10.                                                 %标注曲线

运行结果如图7.22所示。

200-1

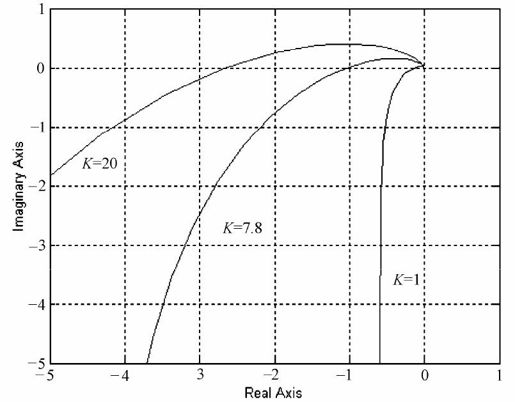
图7.22　例7-8的Nyquist图

该开环系统没有右半S平面的极点（p=0），因此开环系统是稳定的。从图7.22可以看出，当K=1时，开环系统的Nyquist图不包围（-1, j0）点，根据Nyquist稳定判据，系统是稳定的。当K=7.8和K=20时，开环系统的Nyquist图包围（-1, j0）点，根据Nyquist稳定判据，系统是不稳定的。