我的书签
添加书签
移除书签9.3 线性系统的状态可控性与状态可观性
在现代控制理论中，可控性（Controllability）和可观性（Observability）是两个重要的概念，它们是卡尔曼（Kalman）在1960年提出的，是最优控制和最优估计的设计基础。
可观（测）性针对的是系统状态空间模型中状态的可观测性，它表示系统内部状态（通常是不可以直接测量的）可由系统输出量Y(t)（通常是可以直接测量的）反映的能力。
严格地说，可控性分为有两种，一种是系统控制输入U(t)对系统内部状态X(t)的控制能力，另一种是控制输入U(t)对系统输出Y(t)的控制能力。但一般没有特别指明时，指的都是状态的可控性。
系统的可控性和可观性研究一般都基于系统的状态空间表达式。
9.3.1 状态可控性
9.3.1.1 可控的定义
设单输入n阶线性定常离散系统状态方程为：X(k+1)=GX(k)+HU(k)，其中X(k)为n维状态向量；U(k)为1维输入向量；G为n×n系统矩阵；H为n×1输入矩阵。如果存在有限步的控制信号序列U(k)，U(k+1)，…，U(N-1)，使得系统第k步的状态X(k)能在第N步到达零状态，即X(N)=0，其中N是大于k的有限正整数，那么就说系统在第k步的状态X(k)是可控的；如果第k步的所有状态都可控，则称系统在第k步是完全可控的；进一步地，如果系统的每一步都是可控的，则称系统是完全可控的，或称系统为可控系统。
设单输入n阶线性定常连续系统为：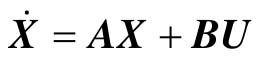
。若存在一个分段连续的控制函数U(t)，能在有限的时间段[0, tf]内把将系统从t0时刻的初始状态X(t0)转移至任意指定的终态X(tf)，则称系统在t0时刻的状态X(t0)是可控的；如果系统每一个状态X(t0)都可控，则称系统是状态完全可控的；反之，只要有一个状态不可控，就称系统是不可控的。
对于线性定常连续系统，为简便起见，可假设t0=0，X(tf)=0，即0时刻的任意初始状态X(0)在有限时间段内转移至零状态（原点）。
9.3.1.2 可控的判据
单输入n阶离散系统可控的充分必要条件是：可控判别阵
的秩等于n，即
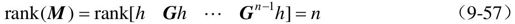
n阶连续系统可控的充分必要条件为可控判别阵
的秩等于n。
对于多输入n阶连续定常系统，
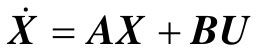
其中，A为n×n阶阵，B为n×r阶阵，U为r维输入。系统可控的充分必要条件为可控判别阵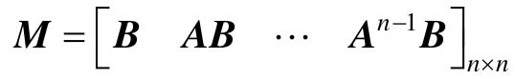
的秩等于n，即rank(M)=n。
对于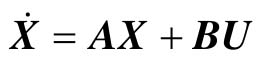
所表示的系统状态方程，如果输入U(t)对状态X(t)的传递函数（阵）没有零极点对消，那么系统可控，否则系统不可控。
对连续系统，
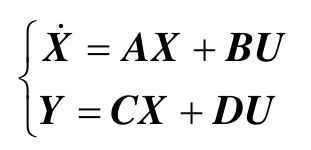
其中，X为n维状态向量，Y为m维输出向量，U为r维控制向量，A为n×m阶阵，B为n×r阶阵，C为m×n阶阵，D为m×r阶阵。如果m×(n+1)r阶矩阵
的秩为m，那么系统是输出可控的。也就是说对任意给定输出初始量Y(t0)，总能找到一个分段连续的控制U(t)，使系统输出能在有限的时间[t0，tf]，段内，转移至任一指定的输出Y(tf)。
9.3.2 状态可观性
9.3.2.1 可观的定义
对于线性定常离散系统，
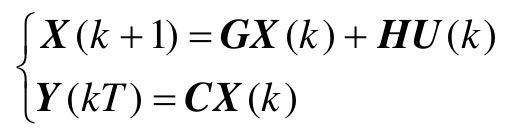
其中，X(k)为n维状态向量；U(k)为1维输入向量；Y(k)为1维输出向量；G为n×n系统矩阵；H为n×1输入矩阵；C为n×1输出矩阵。如果根据第i步以及之后有限步的输出观测y(i), y(i+1),…,y(N)，就能惟一确定第i步的状态X(i)，则称系统是可观的。
对于线性定常离散系统，不失一般性，可设i=0，即从第0步开始观测，确定的是X(0)的值，并且由于U(k)不影响系统的可观性，因此可令U(k)≡0，则系统表示为
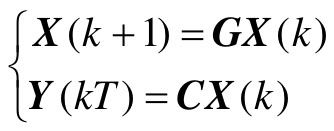
对于线性连续系统，表示为
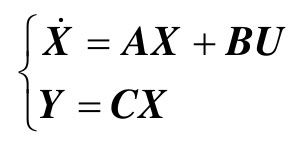
若对任意给定的输入U(t)，总能在有限的时间段[t0，tf]内，根据系统的输入U(t)及系统观测Y(t)，能惟一地确定t0时刻的每一状态X(t0)，那么称系统在t0时刻是状态可观测的。
若系统在所讨论时间段内每一时刻都可观测，则称系统是完全可观测的。
9.3.2.2 可观的判据
对于离散系统，其完全可观的充分必要条件为可观判别阵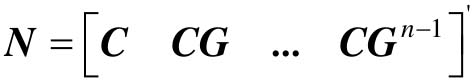
的秩等于n，即rank(N)=n。
线性连续系统完全可观的充分必要条件是可观判别阵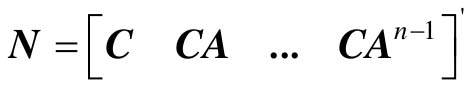
的秩为n。
9.3.3 对偶系统和对偶原理
9.3.3.1 对偶系统
设系统∑1的动态方程为
系统∑2的动态方程为
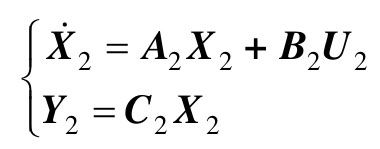
若∑1，∑2满足：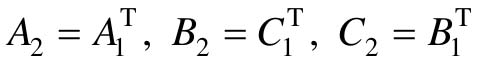
，则称∑1和∑2互为对偶系统。
对偶系统具有以下基本性质：
（1）如果将∑1模拟结构图中信号线反向，即输入端变输出端，输出端变输入端，信号综合点变信号引出点，信号引出点变信号综合点，那么形成的就是∑2的模拟结构图，如图9.12所示。
图9.12 对偶系统结构图
（2）对偶系统的传递函数阵互为转置。
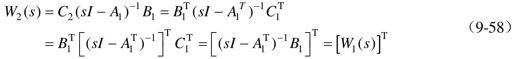
因此，若∑1、∑2为单入单出（SISO）系统，则有W1(s)=W2(s)。
（3）对偶系统特征方程式相同。
9.3.3.2 对偶原理
若系统∑1=(A1,B1,C1)和∑2=(A2,B2,C2)互为对偶系统，则∑1的可控性等价于∑2的可观性，∑1的可观性等价于∑2的可控性，即
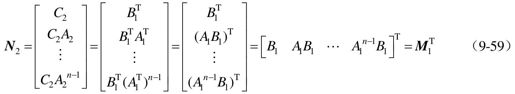
因此rank(N2)=rank(M1)，即∑1的可控性等价于∑2的可观性。
9.3.4 可控标准型和可观标准型
9.3.4.1 可控标准型
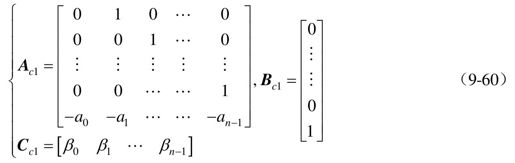
控制系统的可控标准型有两种形式，分别称之为可控Ⅰ型和可控Ⅱ型。
对于可控Ⅰ型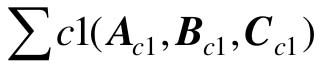
，其各矩阵的形式为
对于可控Ⅱ型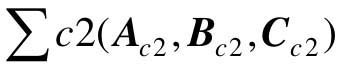
，其各矩阵的形式为
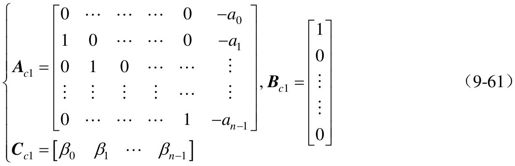
注意
Cc1中的βi与Cc2中的βi不是同一数值。
∑c1的模拟结构图如图9.13所示，∑c2结构图如图9.14所示。
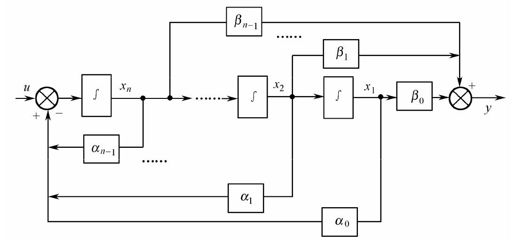
图9.13 可控Ⅰ型模拟结构图
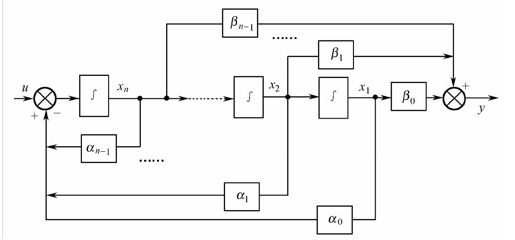
图9.14 可控Ⅱ型模拟结构图
之所以称为可控型，主要是这种形式的动态方程所表示的系统是可控的。
动态方程到可控标准型的转化步骤如下所述。
对于一般动态方程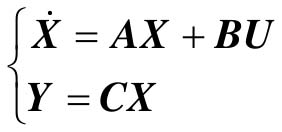
，如果系统可控，即
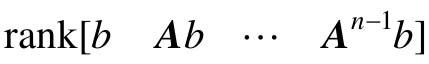满秩，那么可以通过非奇异矩阵
的线性变换，将系统∑(A,B,C)变换成可控Ⅰ型∑c1=(Ac1,Bc1,Cc1)，有
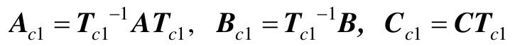
其中，ai(i=0,1,2,…,n-1)是系统特征多项式的系数，即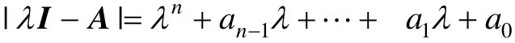
。
由可控Ⅰ型求系统传递函数是非常方便的，因为
由式（9-62）可知，根据系统的传递函数W(s)可直接写出系统的可控Ⅰ型，反之亦然。
对于一般动态系统，如果系统可控，即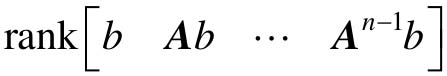
满秩，那么可以通过非奇异变换
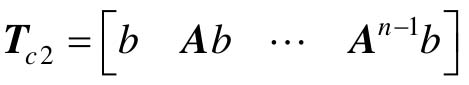将系统∑(A,B,C)变换成可控Ⅱ型
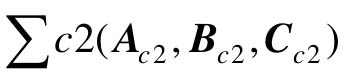，其中，
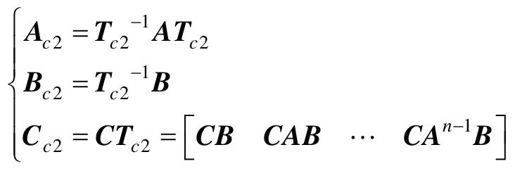
Ac2中的ai(i=0,1,2,…,n-1)是系统特征多项式的系数，即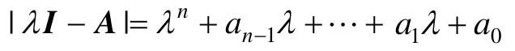
。
9.3.4.2 可观标准型
控制系统的可观标准型也有两种形式，可观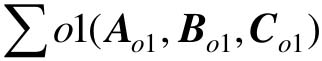Ⅰ型
和可观Ⅱ型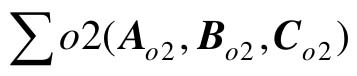
，其中
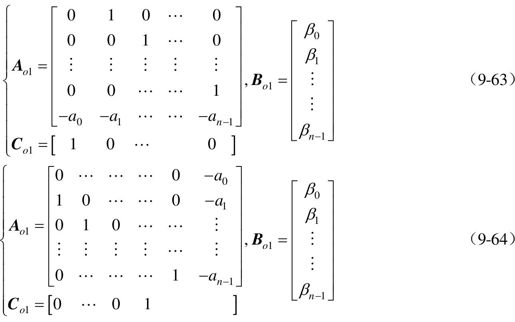
注意
∑o1中的βi与∑o2中的βi不是同一数值。i
可观Ⅰ型∑o1的模拟结构图如图9.15所示，可观Ⅱ型∑o2的模拟结构图如图9.16所示。
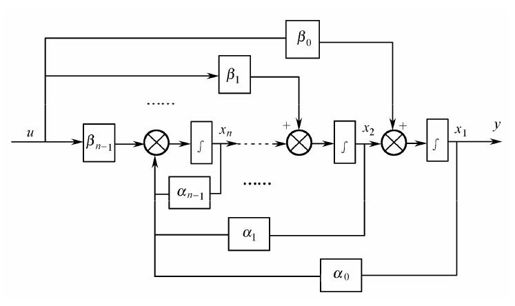
图9.15 可观Ⅰ型模拟结构图
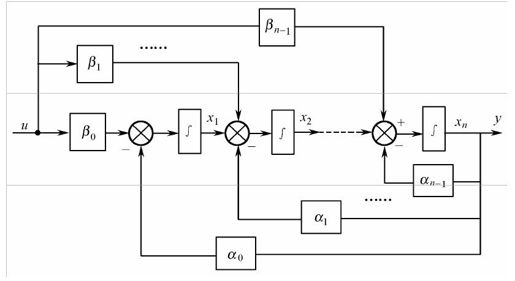
图9.16 可观Ⅱ型模拟结构图
之所以称为可观标准型，主要是这种形式的动态方程所表示的系统是可观的。
动态方程到可观标准型的转化步骤如下所述。
对一般动态方程：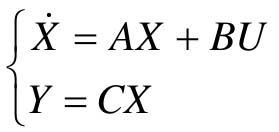
表示的系统，如果系统可观，即系统可观判别阵
满秩，那么可以通过
变换，将系统∑(A,B,C)变换成可观Ⅰ型，其中Bo1中的βi=CAib(i=0,1,2,…,n-1)。
如果系统可观，那么通过矩阵
的线性变换，可以将系统转换成可观Ⅱ型，其中bo2由下列公式求得：
9.3.5 MATLAB在可控和可观标准型中的应用
9.3.5.1 MATLAB中的标准型相关的函数
MATLAB提供了以下4个用于可控和可观标准型的相关应用，下面分别进行介绍。
- 求取系统可控判别矩阵的函数ctrb()
求系统可控判别矩阵M=[B, AB, A2B…]的函数ctrb(A, B)，其常用的调用格式为：
- M= ctrb(A , B)
结合求M秩的函数rank(M)，从而判断系统的能控性。
- 求取系统可观判别矩阵的函数obsv()
求系统可观判别矩阵N=[C, CA, C A2,…]的函数obsv (A, C)，其常用的调用格式为：
- N= obsv (A, C)
结合求N秩的函数rank(N)，从而判断系统的能观性。
- 系统进行能控性分解的函数ctrbf()
当系统能控性矩阵的秩小于系统的维数n时，可以使用函数ctrbf( )对线性系统进行能控性分解，其常用的调用格式为：
- [Ac,Bc,Cc]=ctrbf(A,B,C)
其中，A、B和C是变换前系统矩阵，Ac、Bc和Cc是能控性分解后的矩阵。
- 系统进行能观测性分解的函数obsvf()
当系统能观测性矩阵的秩小于系统的维数n时，可以使用函数obsvf( )对线性系统进行能观测性分解，其常用的调用格式为：
- [Ao,Bo,Co]= obsvf (A,B,C)
其中，A、B和C是变换前系统矩阵，Ao、Bo和Co是能观测性分解后的矩阵。
需要注意的是：当系统的模型用sys=ss(A,B,C,D)输入以后，也就是当系统模型用状态空间的形式表示时，也可以用M=ctrb(sys)，N=obsv(sys)的形式求出该系统的能控性矩阵和能观测性矩阵，与之类似，可以用[Ac,Bc,Cc]=ctrbf(sys)，[Ao,Bo,Co]=obsvf (sys)的形式对该系统的能控性分解和能观测性分解。
9.3.5.2 实例分析
下面通过几个实例讲述上述函数的应用。
【例9-8】 已知系统∑(A,B,C)的相应系统矩阵为
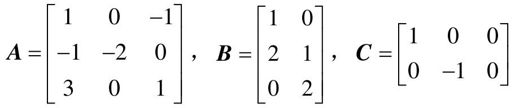
试判断系统是否可控？是否可观？
解：首先分别计算系统的能控性矩阵和能观测性矩阵。然后，再用rank()函数计算这两个矩阵的秩，MATLAB程序代码如下。
- A=[1,0,-1;-1,-2,0;3,0,1]; B=[1,0;2,1;0,2]; C=[1,0,0;0,-1,0]; %系统的系数矩阵
- M=ctrb(A,B) %计算可控判别矩阵
- RM=rank(M) %计算可控判别矩阵的秩
- N=obsv(A,C) %计算可观判别矩阵
- RN=rank(N) %计算可观判别矩阵的秩
运行结果如下：
- M = 1 0 1 -2 -2 -4
- 2 1 -5 -2 9 6
- 0 2 3 2 6 -4
- RM = 3
- N = 1 0 0
- 0 -1 0
- 1 0 -1
- 1 2 0
- -2 0 -2
- -1 -4 -1
- RN = 3
从计算结果可以看出，系统能控性矩阵和能观测性矩阵的秩都是3，为满秩，因此该系统是能控的，也是能观测的。
【例9-9】 已知系统∑(A,B,C,D)的相应系统矩阵为
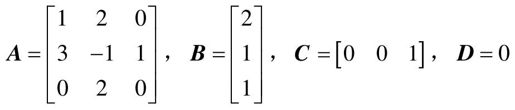
试判断它的可控性，如果完全可控，将其转化为可控II型。
解：MATLAB程序代码如下。
- A=[1, 2, 0;3, -1, 1;0, 2, 0]; B=[2;1;1]; C=[0, 0, 1] ;D=0 %系统的系数矩阵
- T=ctrb(A, B) %计算可控判别矩阵
- R=rank(T) %计算可控判别矩阵的秩
运行结果如下：
- T= 2 4 16
- 1 6 8
- 1 2
- R= 3
由运算结果“R=3”可知，系统完全可控，可以将其转化为可控II型。
接着输入以下MATLAB程序代码：
- [Ac2, Bc2, Cc2, Dc2]=ss2ss(A, B, C, D, inv(T)) %进行状态空间的线性变换
运行结果如下：
- Ac2= 0 0 -2
- 1 0 9
- 0 1
- Bc2= 1
- 0
- 0
- Cc2= 1 2 12
- Dc2= 0
由计算结果可知，该系统的可控II型为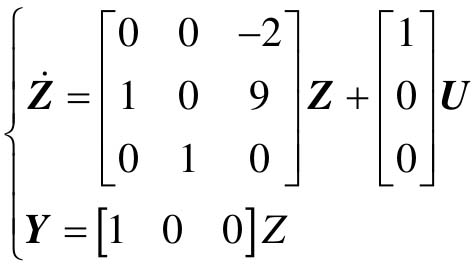
。
【例9-10】 已知系统∑(A,B,C,D)的相应系统矩阵为
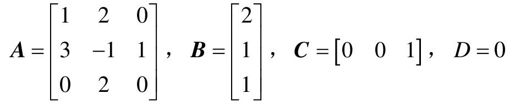
试求该系统的可观I型。
解：MATLAB程序代码如下。
- A=[1, 2, 0;3, -1, 1;0, 2, 0]; B=[2;1;1]; C=[0, 0, 1]; D=0 %系统的系数矩阵
- T=obsv(A, C) %计算可观判别矩阵
- [Ao1, Bo1, Co1, Do1]=ss2ss(A, B, C, D, T) %进行状态空间的线性变换
运行结果如下：
- T= 0 0 1
- 0 2
- 6 -2 2
- Ao1= 0 1 0
- 0 0 1
- -2 9 0
- Bo1=1
- 2
- 12
- Co1= 1 0 0
- Do1= 0
由计算结果可知，该系统的可观I型为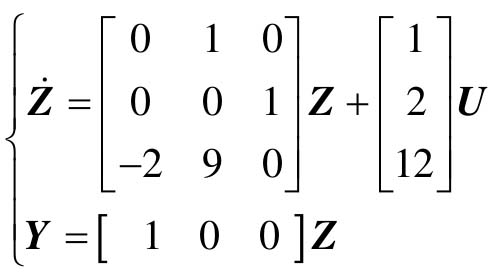
【例9-11】 已知系统∑(A,B,C)的相应系统矩阵为
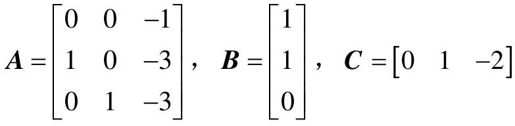
试利用MATLAB对系统进行能控性结构分解和能观测性结构分解。
解：MATLAB程序代码如下。
- A=[0 0 -1;1 0 -3;0 1 -3];B=[1 1 0]';C=[0 1 -2]; % 系统的系数矩阵
- [Ac,Bc,Cc]=ctrbf(A,B,C) % 能控性结构分解
- [Ao,Bo,Co]=obsvf(A,B,C) % 能观测性结构分解运行结果
运行结果如下：
- Ac = -1.0000 0.0000 -0.0000
- -2.1213 -2.5000 0.8660
- -1.2247 -2.5981 0.5000
- Bc = 0
- 0
- -1.4142
- Cc = 1.7321 1.2247 -0.7071
- Ao = -1.0000 -1.3416 -3.8341
- 0.0000 -0.4000 -0.7348
- 0 0.4899 -1.6000
- Bo =1.2247
- -0.5477
- -0.4472
- Co = 0 0.0000 -2.2361
需要注意的是：由MATLAB提供的分解矩阵与前面提到的标准形式不一样，这主要是由于状态变量的编号选取不同，若要得到前面提到的标准形式，只需加下面语句：
- Acc=rot90(Ac,2), Bcc=rot90(Bc,2), Ccc=rot90(Cc,2)
便可得到下面表述形式
- Acc =0.5000 -2.5981 -1.2247
- 0.8660 -2.5000 -2.1213
- -0.0000 0.0000 -1.0000
- Bcc = -1.4142
- 0
- 0
- Ccc = -0.7071 1.2247 1.7321
