12.5　离散控制系统数学模型

要对一个线性离散系统或近似线性离散系统进行分析和设计，首先需要建立相应的系统模型，解决数学描述和分析工具问题。

可用时域数学模型和频域数学模型对线性离散系统进行描述，频域数学模型主要是差分方程，频域数学模型主要是脉冲传递函数。

12.5.1　离散系统时域数学模型

对于一般的线性定常离散系统，如图12.5所示，k时刻的输出y(k)不但与k时刻的输入xk)有关，而且与k时刻以前的输入x(k-1), x(k-2)…有关，同时还与k时刻以前的输出y(k-1), y(k-2)…有关。这种关系可以用下列差分方程描述：

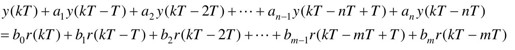
上式可表示为

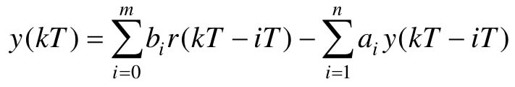
式中，a和b为常数，m<n, k=0, 1, 2,…，称为阶线性常系数差分方程，它在数学上代表一个线性定常离散系统。

差分方程的解法常用方法有迭代法和Z变换法。迭代法非常简单，此处不再赘述。

Z变换法的实质是利用Z变换的实数位移定理，将差分方程化为以z为变量的代数方程，然后进行Z反变换，求出各采样时刻的响应。

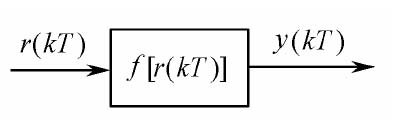
图12.5　线性离散系统模型

Z变换法的具体步骤是：

（1）对差分方程进行Z变换；

（2）解出方程中输出量的Z变换Y(z)；

（3）求Y(z)的Z反变换，得差分方程的解y(k)。

【例12-1】　已知一个离散线性系统的差分方程描述为

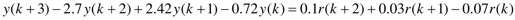
试建立系统的传递函数，显示对象的属性，提取分子和分母多项式，并提取零极点和增益。

解：在零初始条件下，对差分方程进行Z变换，得到系统的传递函数，有

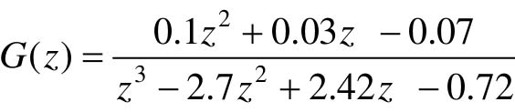
由于系统未指明采样周期，使用命令tf时，它的第3个参数应选为“-1”，表示采样周期T未知；如果T已知，第3个参数则用T值来代替；如果第3个参数完全省略了，则表示系统是连续的或非离散的。

MATLAB程序代码如下：

numG=[0.1 0.03 -0.07]; denG=[1 -2.7 2.42 -0.72];  G=tf(numG, denG, -1) %建立传递函数模型
get(G)                             % 获得模型属性
[n, d]=tfdata(G, 'v')               %提取分子和分母多项式
[z, p, k]=zpkdata(G, 'v')           %提取对象的零极点和增益
pzmap(G)            %画零极点图

MATLAB命令将建立G(z)作为传递函数对象，显示其所有的当前属性，创建两个包括分子、分母多项式系统的列向量nn和dd，并画出零极点图形显示于图12.6中，系统的极点是p1,2,3=0.8,0.9,1.0，零点是z1,2=0.7, -1.0z，增益是0.1。

程序运行结果如下：

Transfer function:
   0.1 z^2 + 0.03 z - 0.07
-----------------------------
z^3 - 2.7 z^2 + 2.42 z - 0.72
nn=        0    0.1000    0.0300   -0.0700  %分子多项式
dd=   1.0000   -2.7000    2.4200   -0.7200   %分母多项式
%系统的零极点和增益
zz =-1.0000
    0.7000
pp =1.0000
    0.9000
    0.8000
kk=0.1000

输出图形如图12.6所示。

图12.6　例12-1的零极点图

12.5.2　离散系统频域数学模型

在线性连续系统中，将初始条件为零时系统（或环节）输出信号的拉氏变换与输入信号的拉氏变换之比定义为传递函数，并用它来描述系统（或环节）的特性。

与此相似，在线性离散系统中，将初始条件为零时系统（或环节）的输出信号Z变换与输入信号的Z变换之比定义为脉冲传递函数，又称为Z传递函数。脉冲传递函数是离散系统的一个重要概念，是分析离散系统的有力工具。

12.5.2.1　脉冲传递函数定义

在零初始条件下，线性定常离散系统的离散输出信号Z变换与离散输入信号Z变换之比称为该系统的脉冲传递函数（或Z传递函数），即

应该指出，多数实际采样系统的输出信号是连续信号，如图12.7所示。在这种情况下，可以在输出端虚设一个采样开关，并设它与输入采样开关以相同的采样周期T同步工作，这样就可以沿用脉冲传递函数的概念。

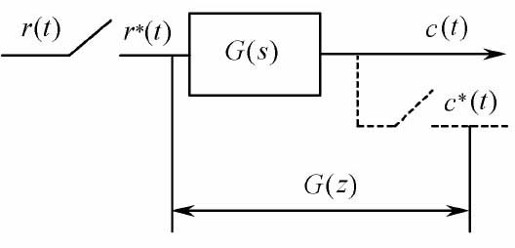
图12.7　采样系统脉冲传递函数

现分析一个孤立的单位脉冲函数δ(t)加在线性对象G(s)上的情况。

由于δ(t)的拉氏变换等于1，所以输出量的拉氏变换为y(s)=G(s)，进一步有y(s)=L-1[G(s)]。习惯上将脉冲响应函数用g(t)表示，即g(t)=L-1[G(s)]。

如果在G(s)上加的是δ(t-a)，即延迟到a时刻才将脉冲函数加上，那么输出信号也自然地延迟一段时间a，而成为δ(t-a)。

再研究一系列脉冲依次作用到G(s)上的情况。

脉冲序列x*(t)可以表示成

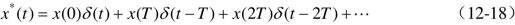
为了求解输出量在各个采样时刻的值，先计算各段时间内的y(t)。

在0≤t<T时间内，实际起作用的只有t=0时刻加入的那一个脉冲，其余各个脉冲尚未加入。因此在这段时间内的输出量是y(t)=x(0)g(t)，将t=0代入上式得y(0)=x(0)g(0)。

在T≤t<2T时间内，y(t)=x(0)g(t)+x(T)g(t-T)，将t=T代入上式得y(T)=x(0)g(t)x(T)g(0)，以此类推，可得出输出在各个采样时刻的值y(kT),(k-0,1,2,…)。

于是y(t)的Z变换为：

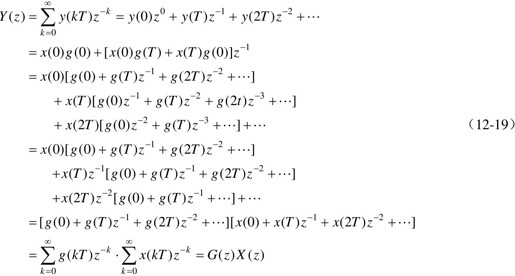
12.5.2.2　脉冲传递函数求解

连续系统或元件的脉冲传递函数G(z)可以通过其传递函数G(s)来求取。

方法是：先求G(s)的拉氏反变换，得到脉冲过渡函数g(t)，再将g(t)按采样周期离散化，得到加权序列g(nT)，最后将g(nT)进行Z变换，得出G(z)。这一过程比较复杂，通常可根据Z变换表，直接从G(s)得到G(z)，而不必逐步推导。

若已知系统的差分方程，则可对方程两端进行Z变换，应用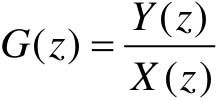求解。

1. 采样拉氏变换的两个重要性质

（1）采样函数的拉氏变换具有周期性，即G(s)=G(s+jkωs)。

（2）若采样函数的拉氏变换与连续函数的拉氏变换相乘后再离散化，则可以从离散符号中提出来，即[G(s)E(s)]=G(s)E(s)。

1. 开环脉冲传递函数

采样系统在开环状态下有两种不同的结构形式，分别如图12.8和图12.9所示。

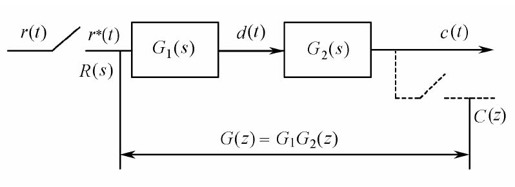
图12.8　中间没有采样开关的两个环节串联

图12.9　中间有采样开关的两个环节串联

串联环节之间有、无采样器时的脉冲传递函数分别为

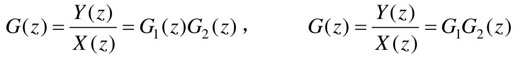
可以看出，被采样开关分隔的两个线性环节串联时，其脉冲传递函数等于这两环节的脉冲传递函数之积。这个结论可以推广到有n个环节串联而各相邻环节之间都有采样开关分离的情形。无采样开关分隔的两个线性环节串联时，其脉冲传递函数等于这两个环节传递函数之积的Z变换。显然，这一结论也可以推广到有n个环节直接串联的情况，但环节之间存在与不存在采样开关时的脉冲传递函数是不相同的。

1. 带有零阶保持器的开环系统脉冲传递函数

设有如图12.10所示的带零阶保持器的开环系统，经简单变换为如图12.11所示的等效的开环系统。

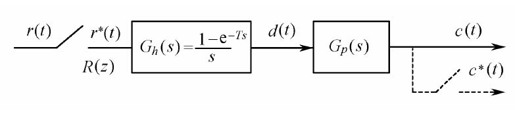
图12.10　带零阶保持器的开环系统

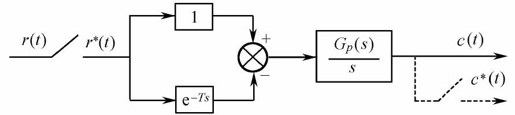
图12.11　带有零阶保持器的开环系统等效图

根据实数位移定理及采样拉氏变换性质，可得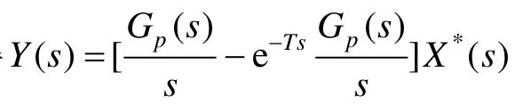，其Z变换式为。

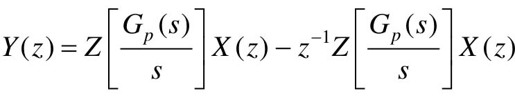于是，有零阶保持器时，开环系统脉冲传递函数为：。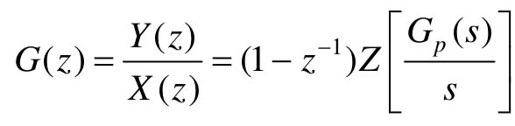

1. 采样系统的闭环脉冲传递函数

在采样系统中，由于设置采样器方式是多种多样的，所以闭环系统的结构形式也不是统一的。图12.12是比较常见的系统结构图，图中输入端和输出端的采样开关是为了便于分析而虚设的。

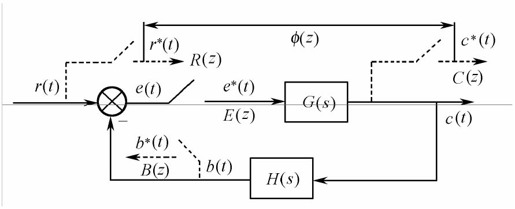
图12.12　采样闭环系统结构示意图

系统闭环脉冲传递函数。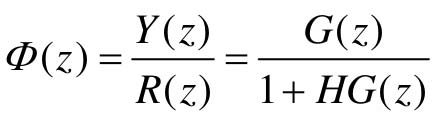

系统闭环误差脉冲传递函数。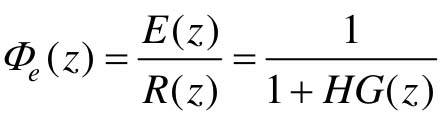

与连续系统类似，令Φ(z)或Φe(z)的分母多项式为零，便可得到离散系统的特征方程为：D(z)=1+HG(z)=0。

需要指出，离散闭环系统脉冲传递函数不能从Φ(z)和Φe(z)求Z变换得来，即。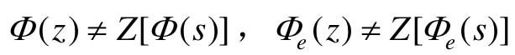

通过与上面类似的方法可以导出采样器为不同配置形式的其他闭环系统脉冲传递函数。但只要误差信号e(t)处没有采样开关，则输入采样信号r*(t)就不存在，此时不能写出闭环系统对于输入量的脉冲传递函数，而只能求出输出采样信号的Z变换函数Y(z)或C(z)。

对于采样开关在闭环系统中具有各种配置的闭环离散系统结构图，以及其输出采样信号Z变换函数Y(z)，此处不再赘述。

MATLAB提供了连续系统和离散系统相互转换的函数，如表12.7所示。

表12.7　连续系统模型与离散系统模型转换函数

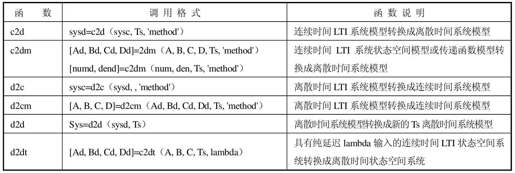
在表12.7中，d表示离散系统（discrete）；c表示连续系统（continuous）；2表示to（转换成的含义，在其他函数中也经常这样使用）；Ts表示采样周期，单位为s。表12.7函数中的'method'表示转换是选用的变换方法，基本含义如表12.8所示，其中，默认的方式是'zoh'。

表12.8　选项'method'的功能说明

【例12-2】　已知一个连续线性系统如图12.13所示，对象模型，试用零阶保持器方法、一阶保持器方法、双线性变换方法和根匹配方法将此连续系统离散化，其中采样周期Ts=0.1s。

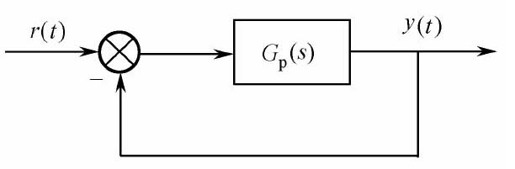
图12.13　例12-2的连续系统结构图

解：MATLAB程序代码如下。

num=[1];  den=[1 1 0];  Gs=tf(num, den)    %建立连续系统传递函数模型
Ts=0.1      %采样周期
Gd1=c2d(Gs, Ts, 'zoh')         %采用零阶保持方法进行系统变换
Gd2=c2d(Gs, Ts, 'foh')      %采用一阶保持方法进行系统变换
Gd3=c2d(Gs, Ts, 'tustin')     %采用双线性变换方法进行系统变换
Gd4=c2d(Gs, Ts, 'matched')     %采用零极点匹配变换方法进行系统变换

运行结果如下：

Transfer function:      %零阶保持方法
0.004837 z + 0.004679
----------------------
z^2 - 1.905 z + 0.9048
Sampling time: 0.1
Transfer function:      %一阶保持方法
0.001626 z^2 + 0.006344 z + 0.001547
------------------------------------
       z^2 - 1.905 z + 0.9048
Sampling time: 0.1
Transfer function:      %双线性变换方法
0.002381 z^2 + 0.004762 z + 0.002381
------------------------------------
       z^2 - 1.905 z + 0.9048
Sampling time: 0.1
Transfer function:      %根匹配变换方法
0.005004 z + 0.005004
----------------------
z^2 - 1.905 z + 0.9048
Sampling time: 0.1

【例12-3】　已知一个连续线性系统如图12.14所示，对象模型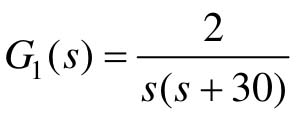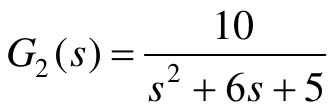，，采样周期Ts=0.1s，试求系统的脉冲闭环传递函数。

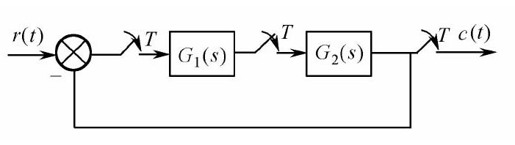
图12.14　例12-3系统结构图

解：MATLAB程序代码如下。

Ts=0.1              %采样周期
num1=[2];   den1=[1, 30, 0];   G1c=tf(num1, den1)
num2=[10];   den2=[1, 6, 5;    G2c=tf(num2, den2)
G1d=c2d(G1c, Ts)        %采用零阶保持方法进行系统变换
G2d=c2d(G2c, Ts)         %采用零阶保持方法进行系统变换
Gd=G1d*G2d   GHd=feedback(Gd, 1)     %建立闭环系统模型

运行结果如下：

Transfer function:      %G1(s)的传递函数
    2
----------
s^2 + 30 s
Transfer function:      %G2(s)的传递函数
     10
-------------
s^2 + 6 s + 5
Transfer function:      %G1(s)转换后的z传递函数
 0.004555 z + 0.00178
----------------------
z^2 - 1.05 z + 0.04979
Sampling time: 0.1
Transfer function:      %G2(s)转换后的z传递函数
 0.04117 z + 0.03372
----------------------
z^2 - 1.511 z + 0.5488
Sampling time: 0.1
Transfer function:      %开环系统的z传递函数
      0.0001875 z^2 + 0.0002268 z + 6e-005
------------------------------------------------
z^4 - 2.561 z^3 + 2.185 z^2 - 0.6514 z + 0.02732
Sampling time: 0.1
Transfer function:      %闭环系统的z传递函数
      0.0001875 z^2 + 0.0002268 z + 6e-005
------------------------------------------------
z^4 - 2.561 z^3 + 2.185 z^2 - 0.6512 z + 0.02738
Sampling time: 0.1