12.4　Z变换

大多数离散控制系统可以用线性离散系统的数学模型来描述，对于线性时不变离散系统，人们习惯用线性定常系数差分方程或脉冲传递函数来表示。线性差分方程的解法主要包括迭代法、古典法和变换法，迭代法和古典法的解法比较麻烦，变换法能把复杂的计算变换成简单的代数运算。

Z变换方法就是一种常用的变换法，在求解差分方程式时，采用Z变换能使求解变得十分简便。Z变换是分析设计离散系统的重要工具之一，它在离散系统中的作用与拉氏变换在连续系统中的作用是相似的。

MATLAB提供了符号运算工具箱（Symbolic Math Toolbox），可方便地进行Z变换和Z反变换，进行Z变换的函数是ztrans，进行Z反变换的函数是iztrans。这部分内容在2.7节进行了详细讲述，此处不再赘述。

12.4.1　离散信号的Z变换

12.4.1.1　Z变换定义

设连续时间函数f(t)可进行拉氏变换，其拉氏变换为F(s)。连续时间函数f(t)经采样周期为T的采样开关后，变成离散信号f*(t)，用数学模型表示为：

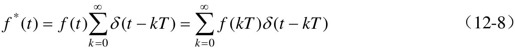
对式（12-8）进行拉氏变换，得

上式中各项均含有e-kTs因子，复变函数-kTs在指数中，且e-kTs是超越函数，因此计算很不方便。

可令z=eTs，其中T为采样周期，z是复数平面上定义的一个复变量，通常称为Z变换算子，可表示为

则得到以z为自变量的函数F(z)

F(z)是复变量z的函数，它表示成一个无穷级数。如果此级数收敛，则序列的Z变换存在。序列的Z变换存在的条件是式（12-11）所定义的级数收敛，以及存在。

若式（12-11）所示级数收敛，则称F(z)是f*(t)的Z变换，记为

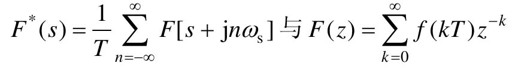是相互补充的两种变换形式，前者表示S平面上的函数关系，后者表示Z平面上的函数关系。

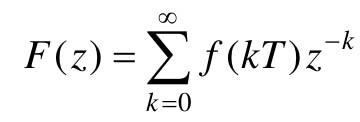所表示的Z变换只适用于离散函数，或者说只能表征连续函数在采样时刻的特性，而不能反映其在采样时刻之间的特性。通常称F(z)是f(t)的Z变换，指的是经过采样后f(t)的Z变换。采样函数f(t)所对应的Z变换是唯一的，反之亦然。但是，一个离散函数f(t)所对应的连续函数却不是唯一的，而是有无穷多个。从这个意义上来说，连续时间函数f(t)与相应的离散时间函数f(t)具有相同的Z变换，即

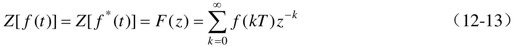
12.4.1.2　Z变换性质定理

Z变换有一些基本定理，可以使Z变换的应用变得简单方便。常用的定理有初值定理、终值定理和卷积定理。

（1）初值定理：如果。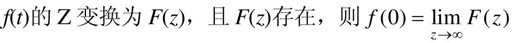

（2）终值定理：如果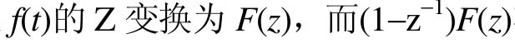在Z平面以原点为圆心的单位圆上和圆外没有极点，则。

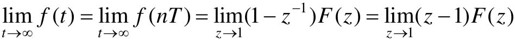（3）卷积定理：如果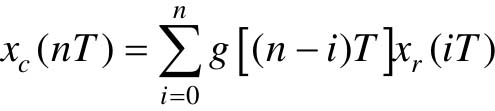，其中n=0, 1, 2,…为正整数，且满足：当n=-1, -2,…时，xc(nT)=0, g(nT)=0, xr)nT)=0，则卷积定理可表示为

式中，。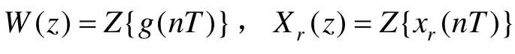

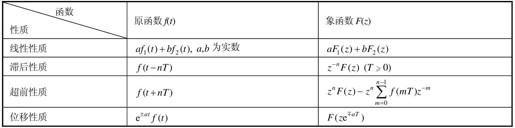
常用的Z变换性质有线性性质、滞后性质、超前性质和位移性质，如表12.5所示。

表12.5　Z变换常用性质

12.4.2　Z变换与Z反变换常用方法

12.4.2.1　Z变换常用方法

求离散时间函数Z变换有多种方法，下面讲述三种常用的Z变换方法。

1. 部分分式法

设连续函数f(t)的拉氏变换式为有理函数F(s)，F(s)可以展开成部分分式的形式：

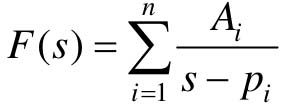
式中，pi为F(s)的极点，Ai为常系数。

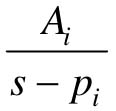对应的时间函数为AiePit，其Z变换为

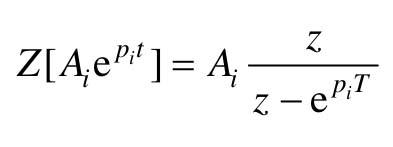
则f(t)的Z变换为

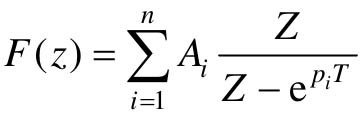
利用部分分式法做Z变换时，应先求出已知连续时间函数f(t)的拉氏变换F(s)，然后将有理分式函数F(s)展开成部分分式之和的形式，最后求出（或查表得到）每一项相应的Z变换。

1. 级数求和法

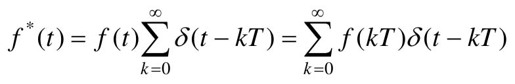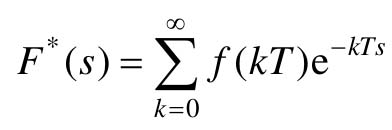根据Z变换定义，由离散函数及其反变换，可得

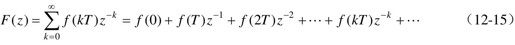
式（12-15）是离散函数Z变换的一种表达形式。只要已知连续函数在采样时刻kT(k=0,1,2,…)的采样值，便可求取离散函数Z变换的级数展开式。对常用离散函数的Z变换应写成级数的求和形式。

通过级数求和法求取已知函数Z变换的缺点在于需要将无穷级数写成和式。这在某些情况下要求具有很高的技巧。但函数Z变换的无穷级数形式具有鲜明的物理含义，这又是Z变换无穷级数表达形式的优点。

Z变换本身便包含着时间概念，可由函数Z变换的无容级数形式清楚地看出原连续函数采样脉冲序列的分布情况。

1. 留数法

如果已知连续信号f(t)的拉氏变换F(s)及它的全部极点，则可用下列留数计算公式求取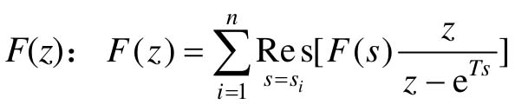，函数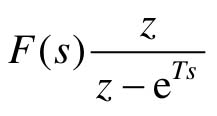在极点处的留数计算方法如下：

若si为单极点，则

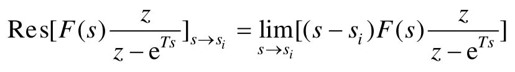
若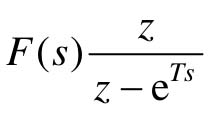有ri重极点si，则

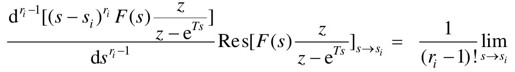
12.4.2.2　Z反变换常用方法

与拉氏反变换类似，Z反变换可表示为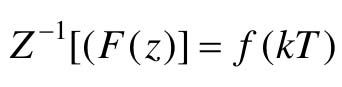：。下面介绍三种常用的Z反变换法。

1. 综合除法

这种方法是用F(z)的分母除分子。求出z-1按升幂排列的级数展开式，然后用反变换求出相应的采样函数的脉冲序列。

F(z)可表示为

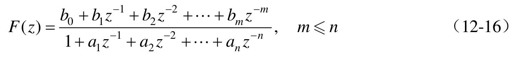
式中，ai、bj均为常系数。

通过对式（12-16）直接做综合除法，可得按z-1升幂排列的幂级数展开式。如果得到的无穷级数是收敛的，则按Z变换定义可知上式中的系数fk(k=0,1,…)就是采样脉冲序列f*(t)的脉冲强度f(kT)。

这样就可直接写出f(t)的脉冲序列表达式为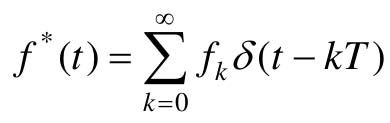：，它就是要求通过Z反变换得到的离散信号f(t)。

使用综合除法有几点要注意：

（1）在进行综合除法之前，必须先将F(z)的分子、分母多项式按z的降幂形式排列。

（2）实际应用中，常常只需计算有限的几项就够了，因此用综合除法计算f*(t)最简便，这是它的优点之一。

（3）要从一组f(kT)值中求出通项表达式，通常是比较困难的。

1. 部分分式展开法

在Z变换表中，所有Z变换函数F(z)在其分子上都普遍含有因子z，所以应将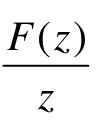展开为部分分式，然后将所得结果每一项都乘以z，即得F(z)的部分分式展开式。

1. 留数计算法

根据Z变换定义有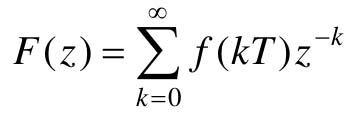，根据柯西留数定理有，式中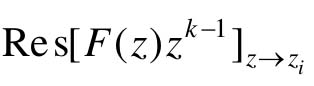表示F(z)zk-1在极点zi处的留数。

函数F(z)zk-1在极点处的留数计算方法如下：

若zi为单极点，则

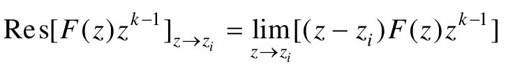
若F(z)zk-1有ri阶重极点，则

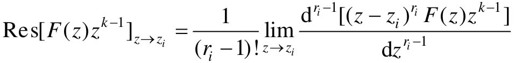
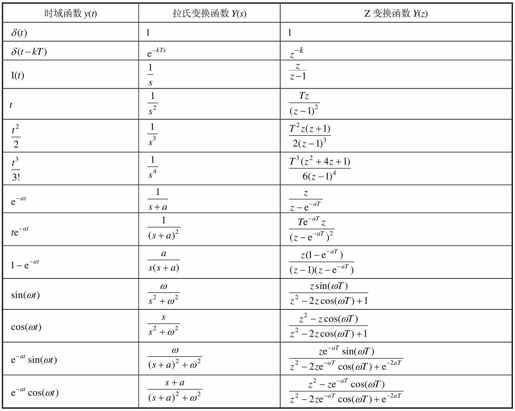
常用时间函数的Z变换如表12.6所示，供在进行相应函数Z变换时查阅。

表12.6　常用函数Z变换表