13.2　最优控制问题的描述

给定连续时间控制系统为

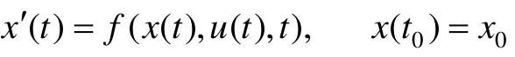
式中，x(t)是状态向量，u(t)是控制向量，f(x(t),u(t),t)是x(t),u(t)和t的连续函数。最优控制问题就是在保证系统从已知的初始状态x(t0)转移到预定的目标状态x(tf)的情况下，寻求最优的控制函数u(t)，使性能指标取最小值。

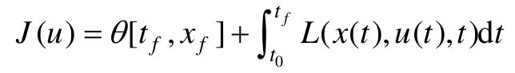
有时，性能指标也可以采用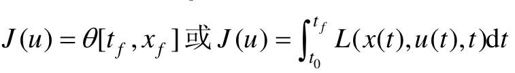的形式。

上面的形式是末指型性能指标，表示系统在控制过程结束后，终端状态需要满足一定的需求。比如希望被控对象精确停止在空间中的某一位置、被控对象的温度尽可能地靠近设定值等。终端时间tf可以固定，也可以是自由的，这由控制问题的性质所决定。

下面的形式则是最一般的性能指标形式，表示不仅对控制过程结束后的终端状态有一定的要求，还需要整个控制过程满足特定的条件。

中的被积函数L(x(t),u(t),t)还可以有多种形式。比如取L(x(t),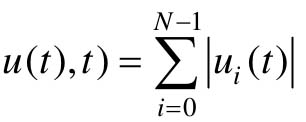，那么J(u)就表示整个控制过程所消耗的能量。此时，最优控制的目标就是使系统消耗的能量最小。这是航天工程中最常见的问题，比如登月飞行器在进行软着陆时，需要发动机产生一个与月球重力相反方向的推力；希望飞行器在着陆过程中消耗最小的燃料，进而减轻飞行器的重量，就是这类最优控制问题。

当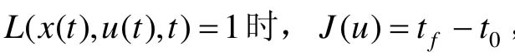，此时最优控制问题的目标就是使整个控制过程的时间最短。

L(x(t),u(t),t)的不同形式就代表了不同的优化目标。这里提到的只是几种常见的形式而已。

对于离散时间控制系统，相应的最优控制问题可以描述为

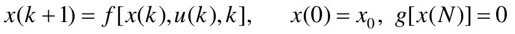
式中，g[x(N)]为表示末状态约束的向量函数。此时，最优控制问题就是求最优的控制序列u(k),k-0,1,2,…,N-1，使性能指标

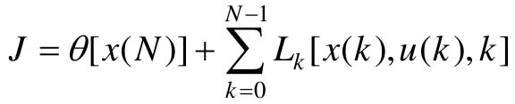
取最小值。

最优控制问题有多种解法。当性能指标、约束条件形式简单时，适合用解析法，将优化问题转化为一组方程或不等式，进行求解；当性能指标比较复杂，难以解析时，可以采用数值方法，通过迭代，逐步逼近理论解。二者相结合使用就是梯度型法。