8.5　控制系统校正的频率响应法

前文提到对数频率特性的低频段影响系统的稳态误差，当要求系统的输出量以某一精度跟随输入时，需要系统在低频段具有相当的增益；在中频段，为了保证系统有足够的相位裕量，其特性斜率应为-20 dB/dec，一般最大不超过-30 dB/dec，而且在穿越频率附近要有一定的延伸段；为了减小高频干扰的影响，通常需要有尽快衰减的特性。

8.5.1　基于频率法的超前校正

频率法中的串联超前校正是利用校正装置的超前相位在穿越频率处对系统进行相位补偿，以提高系统的相位稳定裕量，同时也提高了穿越频率值，从而改善系统的稳定性和快速性。串联超前校正主要适用于稳定精度不需要改变，暂态性能不佳，而穿越频率附近相位变化平稳的系统。

应用频率法进行串联超前校正的步骤如下：

（1）根据所要求的稳态性能指标，确定系统的开环增益K。

（2）绘制满足由（1）确定的值下的系统Bode图，并求出系统的相角裕量γ0。

（3）确定为使相角裕量达到要求值所需增加的超前相角ϕc，即ϕc=γ-γ0+ε，其中，γ为要求的相角裕量，是考虑到校正装置影响剪切频率的位置而附加的相角裕量，当未校正系统中频段的斜率为-40 dB/dec时，取ε=5°～15°，当未校正系统中频段斜率为-60 dB/dec时，取ε=5°～20°。

（4）令超前校正网络的最大超前相角ϕm=ϕc，则由下式求出校正装置的参数α。

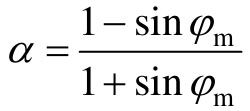
P_231-1

（5）在Bode图上确定未校正系统幅值为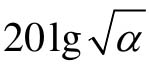H_0019时的频率ωm，该频率作为校正后系统的开环剪切频率ωc，即ωc=ωm。

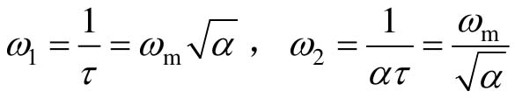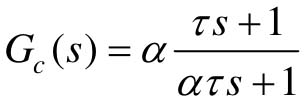（6）由ωm确定校正装置的转折频率ω1和ω2。H_0020。超前校正装置的传递函数H_0021。

（7）将系统放大倍数增大1/α倍，以补偿超前校正装置引起的幅值衰减，即Kc=1/α。

（8）画出校正后系统的Bode图，校正后系统的开环传递函数为G(s)=Go(s)Gc(s)Kc。

（9）检验系统的性能指标，若不满足要求，可增大ε值，从步骤（3）重新计算。

8.5.2　基于频率法的滞后校正

频率法中的串联滞后校正在于提高系统的开环增益，改善控制系统的稳态性能，而尽量不影响原有系统的动态性能。串联滞后校正主要适用于未校正系统或经串联超前校正的系统的动态性能不能满足给定性能指标的需要，只需增大开环增益用以提高控制系统精度的一类系统中。

基于频率法的串联滞后校正步骤如下：

（1）根据稳态误差的要求确定系统开环放大系数，再用这一放大系数绘制原系统的Bode图，计算出本校正系统的相位裕量和增益裕量。

（2）根据给定相位裕量，增加5°～15°的补偿，估计需要附加的相角位移，找出符合这一要求的频率作为穿越频率ωc。

（3）确定出原系统在ω=ωc处幅值下降到零分贝时所必需的衰减量。使这一衰减量等于-201gγi，从而确定γi的值。

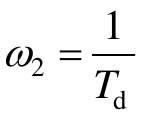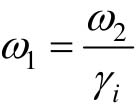（4）选择H_0022，计算H_0023。

（5）计算校正后频率特性的相位裕量并判断是否满足给定要求，若不满足则重新计算。

（6）计算校正装置参数。

8.5.3　MATLAB/Simulink在频率响应法校正中的应用

根据前面所讲的频率响应法校正设计原则，可以采用MATLAB编写校正函数，调用函数便可设计出所需的校正器，为线性控制系统的设计提供了一种简单有效的途径。下面通过实例介绍用MATLAB实现校正器的频率响应法设计的详细过程。

【例8-11】　已知系统开环传递函数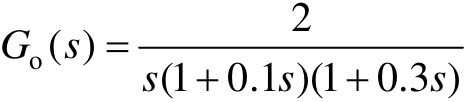H_0024，试设计超前校正环节，使其校正后系统的静态速度误差系数Kv≤6，相角裕度为45°，并绘制校正前后系统的单位阶跃响应曲线，开环Bode图和闭环Nyquist图。

解：计算串联超前校正环节参数的子函数MATLAB程序代码如下。

  1. %采用频率响应法设计的串联超前校正的子函数
  2. %G为校正前系统的开环传递函数；Gc为校正环节的传递函数
  3. function Gc=cqjz_frequency(G, kc, yPm)
  4. G=tf(G)
  5. [mag, pha, w]=bode(G*kc);   Mag=20*log10(mag)
  6. [Gm, Pm.Wcg, Wcp]=margin(G*kc)
  7. phi=(yPm-getfield(Pm, 'Wcg'))*pi/180; alpha=(1+sin(phi))/(1-sin(phi)
  8. Mn=-10*log10(alpha);   Wcgn=spline(Mag, w, Mn)
  9. T=1/Wcgn/sqrt(alpha); Tz=alpha*T
  10. Gc=tf([Tz, 1], [T, 1])

主函数MATLAB代码如下：

  1. num=2; den=conv([1, 0], conv([0.3, 1], [0.1, 1]) ); G=tf(num, den)
  2.             %建立校正前系统的开环传递函数
  3. kc=3;  yPm=45+12
  4. Gc=cqjz_frequency(G, kc, yPm)      %求得串联超前校正环节的传递函数
  5. G=G*kc;  GGc=G*Gc
  6. Gy_close=feedback(G, 1)        %校正前系统的闭环传递函数
  7. Gx_close=feedback(GGc, 1)       %校正后系统的闭环传递函数
  8. figure(1);  step(Gx_close, 'b');  hold on    %绘制校正后系统的单位阶跃响应图
  9. step(Gy_close, 'r');  grid       %绘制校正前系统的单位阶跃响应图
  10. gtext('校正前的'); gtext('校正后的')    %放置曲线的文字注释
  11. figure(2);  bode(G, 'b');  hold on      %绘制校正前系统的Bode图
  12. bode(GGc, 'r');  grid         %绘制校正后系统的Bode图
  13. gtext('校正前的'); gtext('校正后的'); gtext('校正前的'); gtext('校正后的');
  14.             %放置曲线的文字注释
  15. figure(3);  nyquist(Gx_close, 'b');  hold on  %绘制校正后系统的Nyquist图
  16. nyquist(Gy_close, 'r');  grid      %绘制校正前系统的Nyquist图
  17. gtext('校正前的'); gtext('校正后的')     %放置曲线的文字注释

运行结果如下：

  1. %超前校正环节传递函数
  2. Transfer function:
  3. 0.3611 s + 1
  4. -------------
  5. 0.09471 s + 1
  6. %校正后系统闭环传递函数
  7.     2.167 s + 6
  8. ----------------------------------------------------
  9. 0.002841 s^4 + 0.06788 s^3 + 0.4947 s^2 + 3.167 s +

系统校正前后的单位阶跃响应曲线如图8.42所示。

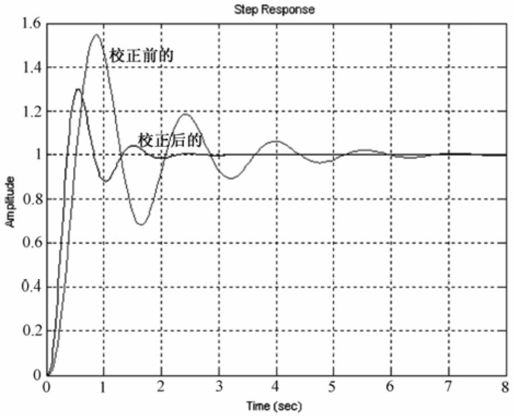
P_233-1

图8.42　例8-11系统校正前后单位阶跃响应曲线

系统校正前后的开环Bode图如图8.43所示。

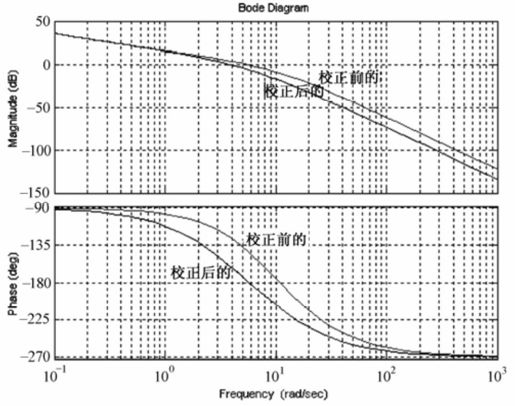
P_233-2

图8.43　例8-11系统校正前后开环Bode图

系统校正前后的闭环Nyquist图如图8.44所示。

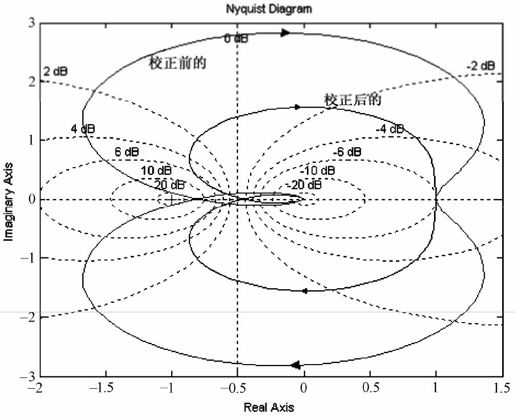
P_234-1

图8.44　例8-11系统校正前后闭环Nyquist图

由运行结果可知，串联超前校正环节的传递函数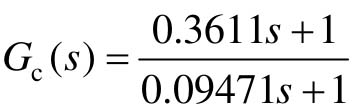H_0025。在Bode图上单击鼠标右键，选择弹出菜单“Charateristics”，选择“Stability”便可得到系统的幅值裕度、相角裕度和调节时间。由运行图可知，校正前的幅值裕度为6.94 dB，相角裕度为21.2；校正后的系统幅值裕度为10.1 dB，相角裕度为39，可知引入串联超前校正后，系统的带宽增加，闭环系统谐振峰值下降，静态误差系数增大。

【例8-12】　已知系统开环传递函数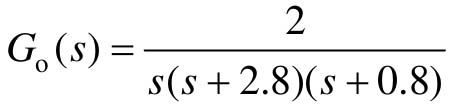H_0026，试设计滞后校正环节，使其校正后系统的静态速度误差系数Kv≤6，系统阻尼比ζ=0.307，并绘制校正前后系统的单位阶跃响应曲线，开环Bode图和闭环Nyquist图。

解：计算串联滞后校正环节参数的子函数MATLAB程序代码如下。%采用频率响应法设计的串联滞后校正的子函数

  1. %采用频率响应法设计的串联滞后校正的子函数
  2. %G为校正前系统的开环传递函数； Gc为校正环节的传递函数
  3. function Gc=cqjz_frequency(G, kc, dPm)
  4. G=tf(G);  num=G.num{1}; den=G.den{1}
  5. [mag, phase, w]=bode(G*kc)
  6. wcg=spline(phase(1, :), w', dPm-180)
  7. magdb=20*log10(mag)
  8. Gr=-spline(w', magdb(1, :), wcg)
  9. alpha=10^(Gr/20); T=10/(alpha*wcg)
  10. Gc=tf([alpha*T, 1], [T, 1])

主函数MATLAB代码如下：

  1. num=2;  den=conv([1, 0], conv([1, 2.8], [1, 0.8]));  G=tf(num, den)
  2. zeta=0.307;  Pm=2*sin(zeta)*180/pi
  3. dPm=Pm+5;  kc=2
  4. Gc=zhjz_frequency(G, kc, dPm)
  5. G=G*kc; GGc=G*Gc           %获得校正后系统的开环传递函数
  6. Gy_close=feedback(G, 1)         %校正前系统的闭环传递函数
  7. Gx_close=feedback(GGc, 1)         %校正后系统的闭环传递函数
  8. figure(1);  step(Gx_close, 'b');  hold on;    %绘制校正后系统的单位阶跃响应图
  9. step(Gy_close, 'r');  grid        %绘制校正前系统的单位阶跃响应图
  10. gtext('校正前的');   gtext('校正后的')       %放置曲线的文字注释
  11. figure(2);  bode(G, 'b');  hold on      %绘制校正前系统的Bode图
  12. bode(GGc, 'r');   grid        %绘制校正后系统的Bode图
  13. gtext('校正前的'); gtext('校正后的'); gtext('校正前的'); gtext('校正后的');
  14.              %放置曲线的文字注释
  15. figure(3);  nyquist(Gx_close, 'b');  hold on  %绘制校正后系统的Nyquist图
  16. nyquist(Gy_close, 'r');  grid        %绘制校正前系统的Nyquist图
  17. gtext('校正前的');  gtext('校正后的')      %放置曲线的文字注释

运行结果如下：

  1. %滞后校正环节传递函数
  2. 16.08 s + 1
  3. -----------
  4. 35.61 s + 1
  5. %校正后系统闭环传递函数
  6.          64.34 s + 4
  7. ----------------------------------------------
  8. 35.61 s^4 + 129.2 s^3 + 83.37 s^2 + 66.58 s +

系统校正前后的单位阶跃响应曲线如图8.45所示。系统校正前后的Bode图如图8.46所示。系统校正前后的Nyquist图如图8.47所示。

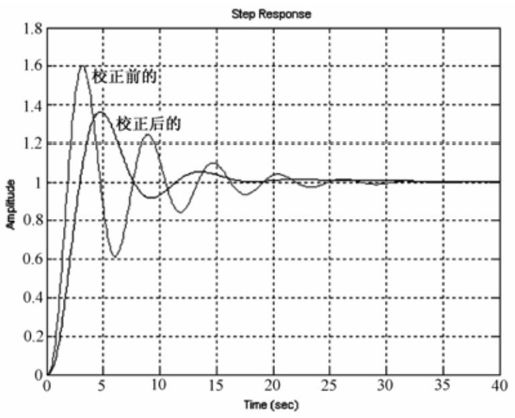
P_235-1

图8.45　校正前后闭环系统的单位阶跃响应曲线

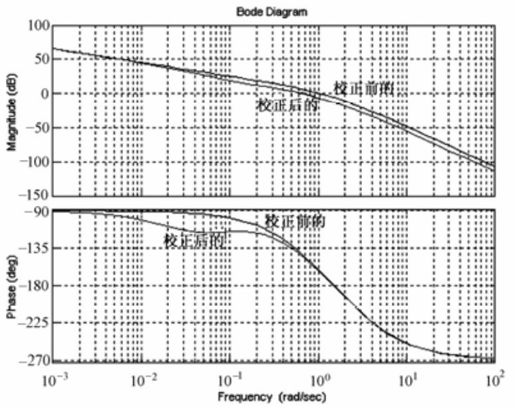
P_235-2

图8.46　校正前后开环系统的Bode图

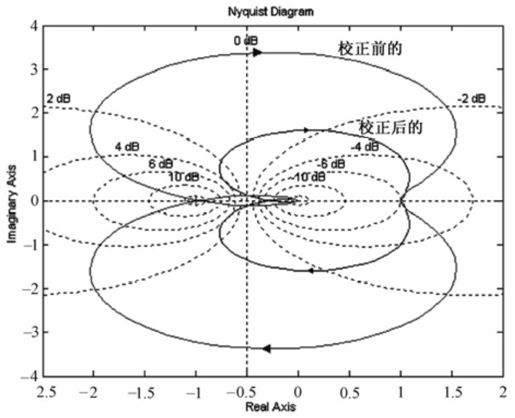
P_236-1

图8.47　校正前后闭环系统的Nyquist图

由运行结果可知，串联滞后校正环节的传递函数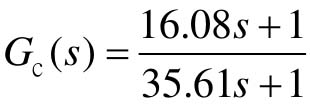H_0027。在Bode图上单击鼠标右键，选择弹出菜单“Charateristics”，再选择“Stability”便可得到系统的幅值裕度、相角裕度和调节时间。由运行图可知，校正前的幅值裕度为6.09 dB，相角裕度为17.7；校正后的系统幅值裕度为12.5 dB，相角裕度为36.4，系统的幅值裕度和相角裕度都得到了改善。

频率法中的串联超前滞后校正，可兼有上述两种作用，主要用于要求较高但单纯的超前校正或滞后校正不能满足或无法应用的系统的校正，设计方法与前面类似，此处不再赘述。