8.6 综合实例及MATLAB/Simulink应用
下面通过一个综合实例,讲述MATLAB/Simulink在本章中的应用。
【例8-13】 某单位负反馈控制系统的开环传递函数 ,设计一个串联的校正装置,使校正后的系统静态速度误差系数≥10s-1,相角裕量≥45,增益裕量≥10 dB。
,设计一个串联的校正装置,使校正后的系统静态速度误差系数≥10s-1,相角裕量≥45,增益裕量≥10 dB。
解:使用MATLAB/Simunlink求解本题的基本步骤如下。
【步骤1】 确定开环传递函数中的系数K。
系统的静态速度误差系数的计算公式为:
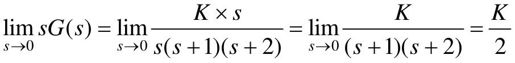
根据题目要求,校正后的系统静态速度误差系数最小为10s-1,因此可求得K=20。
因此,系统的开环传递函数为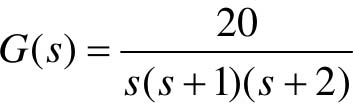 。
。
【步骤2】 建立控制系统的数学模型。
MATLAB的代码如下:
- clc; % 清除工作空间显示
- clear; % 清除工作空间的所有变量
- num_open = [0 20]; % 开环传递函数分子多项式系数
- den_open = conv(conv([1 0],[1 1]),[1 2]); % 开环传递函数分母多项式系数
- sys_open = tf(num_open,den_open) % 开环传递函数模型
程序运行的结果为:
- Transfer function:
- 20
- --------------------
- s^3 + 3 s^2 + 2 s
【步骤3】 分析系统的动态特性。
根据建立好的数学模型,绘制系统的频率响应曲线,分析系统的动态特性。利用margin命令计算闭环系统当前的相角裕量和增益裕量,以此确定所需的串联校正环节。
MATLAB代码如下:
- % 分析系统的频率响应特性
- [Gm, Pm, Wcg, Wcp] = margin(sys_open) % 计算相角裕量和增益裕量
- margin(sys_open);
程序的运行结果为:
- Gm = -10.50
- Pm = -28.0814
- Wcg = 1.4142
- Wcp = 2.4253
系统频率响应曲线如图8.48所示。
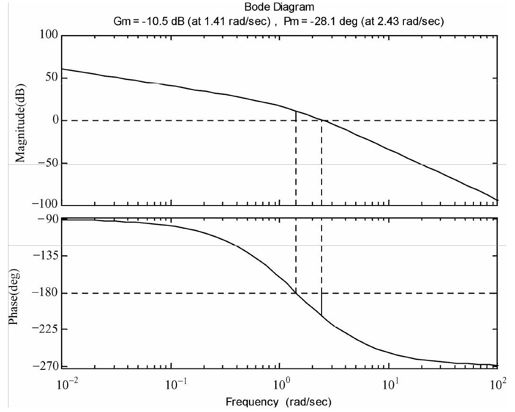
图8.48 闭环系统的频率响应曲线
计算结果显示,未校正的系统增益裕量只有-10.5,相角裕量为-28.0814;相角穿越频率为1.4142,幅值穿越频率为2.4253。系统尚不稳定,离题设要求的性能相去甚远。因此,需要串联校正环节,使系统的动态特性满足要求。
【步骤4】 设计系统的串联校正装置。
由于系统期望相角裕量为45,因此校正装置需要将相角提升大约73。如果单纯采用超前校正,则很难提升如此之大的相角;如果单纯采用滞后校正,则系统的增益裕量又会下降(目前的增益裕量尚且没有满足题设的要求)。综合考虑,需要采用超前滞后校正。
首先设计滞后环节。假定校正后的系统增益穿越频率为1,并且取零极点之比为10,则滞后环节的传递函数为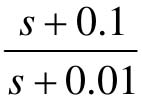 。此时,系统的频率响应如图8.49所示。
。此时,系统的频率响应如图8.49所示。
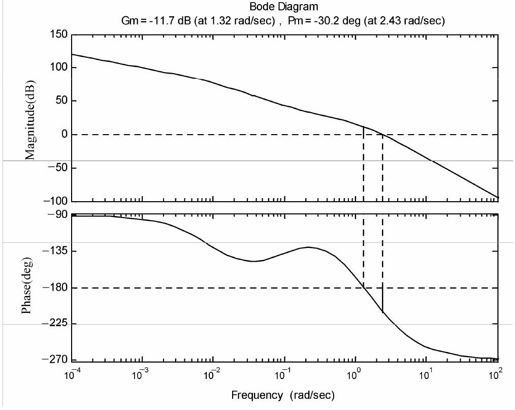
图8.49 加入滞后环节后的系统频率响应曲线
对应的MATLAB代码如下:
- % 设计串联校正器的滞后环节
- num_zhihou = [1 0.1]; %滞后环节传递函数的分子多项式系数
- den_zhihou = [1 0.01]; %滞后环节传递函数的分母多项式系数
- sys_zhihou = tf(num_zhihou, den_zhihou); %滞后环节的传递函数模型
- sys_new = sys_open * sys_zhihou %加入滞后环节后系统的开环传递函数
- margin(sys_new); %绘制加入滞后环节后系统的Bode曲线
随后,根据滞后校正得出的结果,相应设计超前校正环节为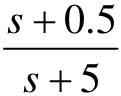 。此时,系统的频率响应如图8.50所示。
。此时,系统的频率响应如图8.50所示。
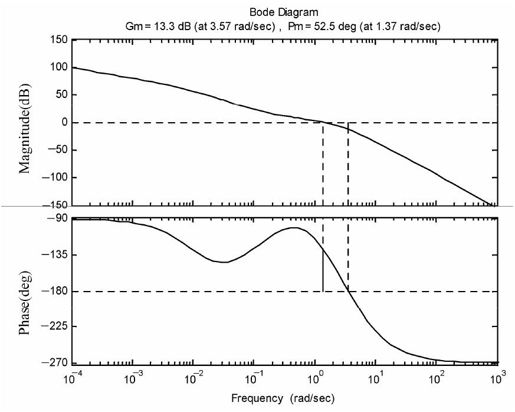
图8.50 加入超前滞后校正环节后系统的频率响应曲线
对应的MATLAB代码如下:
- % 设计串联校正器的超前环节
- num_chaoqian = [1 0.5]; den_chaoqian = [1 5]; %超前环节传递函数的分子、分母多项式系数
- sys_chaoqian = tf(num_chaoqian,den_chaoqian); %超前环节的传递函数模型
- sys_new = sys_new * sys_chaoqian; %加入超前-滞后环节后系统的开环传递函数
- margin(sys_new); %绘制加入超前-滞后环节后系统的Bode曲线
不难看出,此时闭环系统的增益裕量为13.3,相角裕量为52.5,增益穿越频率为1.37;各项参数均符合题设要求。
利用如下MATLAB代码,可以对比校正前后系统的频率响应:
- % 对比校正前后的系统频率响应
- figure(1); %开启新的图形显示窗口
- bode(sys_open); %绘制开环传递函数的Bode曲线
- hold on; %在同一幅图像上显示多条曲线
- bode(sys_new); %绘制加入校正环节后系统的Bode曲线
- gtext('校正前的'); gtext('校正后的'); gtext('校正前的'); gtext('校正后的');
- %为曲线添加标注
- grid on %显示网格线
程序运行的结果如图8.51所示。
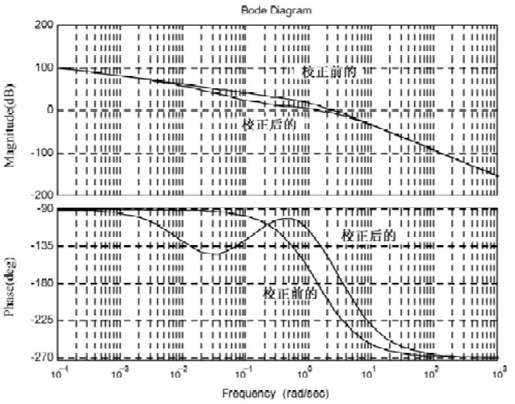
图8.51 系统校正前后不同的频率响应曲线
从图8.51中可以看出:超前滞后校正环节主要作用于0.01~10频率段;滞后校正将低频部分的相频曲线“压低”,超前校正则将高频部分的相频曲线“抬高”,从而大大提高了系统中频段的相位。
同时,滞后校正“抬高”低频部分的幅频曲线,而超前校正“压低”从低频开始较广频率范围的幅频曲线,这又使得系统的增益频率左移。双重作用下,系统的相角裕量大大增加。
此外,相角穿越频率右移,使系统的增益裕量进一步提高。超前滞后校正较好的满足了题设的要求。当然,这些是以牺牲系统的增益穿越频率为代价的。
综上,校正后的系统开环传递函数为:
- Transfer function:
- 20 s^2 + 12 s + 1
- --------------------------------------------------------
- s^5 + 8.01 s^4 + 17.08 s^3 + 10.17 s^2 + 0.1
【步骤5】 比较校正前后系统的性能。
比较一下校正前后系统的阶跃响应。
MATLAB代码如下:
- % 系统校正前后的阶跃响应曲线
- figure(2); % 开启新的图形显示窗口
- step(feedback(sys_open,1)); % 绘制原始闭环系统的阶跃响应曲线
- grid on; % 显示网格线
- figure(3); % 开启新的图形显示窗口
- step(feedback(sys_new,1)); % 绘制校正后闭环系统的阶跃响应曲线
- gtext('校正前的'); gtext('校正后的'); % 为曲线添加标注
- grid on; % 显示网格线
程序运行的结果如图8.52和图8.53所示。
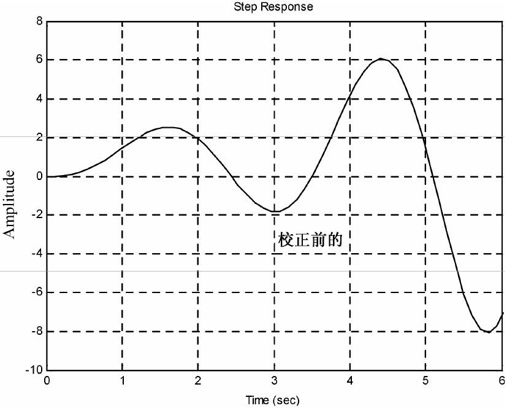
图8.52 系统校正前的阶跃响应曲线
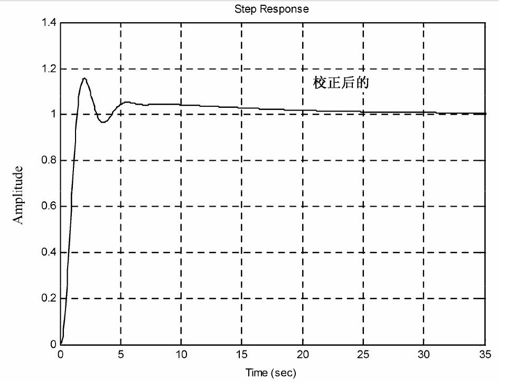
图8.53 系统校正后的阶跃响应曲线
可见,校正环节的加入,使得系统由不稳定变得动态特性良好。
【步骤6】 顺便指出,还可以采用在第7章中提过的rltool工具进行校正。在rltool中可以很方便地放置零极点,通过观察系统的频率响应曲线,不断调节零极点的位置,直到系统的频率特性符合要求。此时,可从界面中直接读取出校正环节的传递函数,非常简捷。
MATLAB命令为rltool(sys_open)。校正后的结果如图8.54所示,具体过程不再赘述。
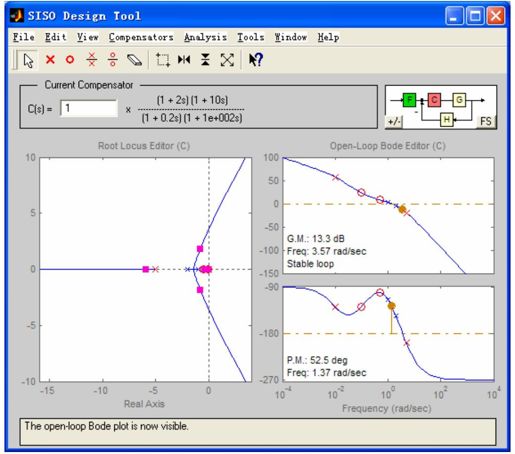
图8.54 利用rltool进行校正环节设计
习 题
【8.1】 给定单位负反馈控制系统,被控对象的传递函数 。
。
(1)利用MATLAB建立控制系统的数学模型,并绘制其幅频特性曲线;
(2)设计一个滞后校正装置,使得系统的相角裕量达到45°。
(提示:采用Bode图校正方法)
【8.2】 已知某单位负反馈控制系统的开环传递函数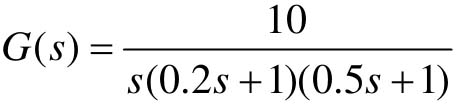 。
。
(1)利用MATLAB建立控制系统的数学模型,并绘制其幅频特性曲线;
(2)设计一个超前校正装置,使系统的静态速度误差系数为Kv=10s-1,相角裕量不小于50°;
(3)设计一个滞后校正装置,使系统的静态速度误差系数为Kv=10s-1,相角裕量不小于50°;
(4)比较两种校正效果的差别。
(提示:采用Bode图校正方法)
【8.3】 已知某单位负反馈控制系统的开环传递函数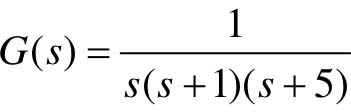 。
。
(1)利用MATLAB建立控制系统的数学模型,并绘制出其幅频特性曲线,计算其相角裕量、增益裕量、幅值穿越频率和相角穿越频率等参数;
(2)设计一个超前滞后校正环节,保证系统的静态速度误差系数为Kv=20s-1,相角裕量不小于60°,并且增益裕量大于等于8 dB。
(提示:采用Bode图校正方法)
【8.4】 已知某单位负反馈控制系统的开环传递函数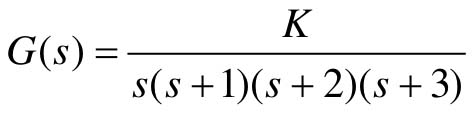 。
。
(1)利用MATLAB建立控制系统的数学模型,并绘制其根轨迹曲线,确定使系统稳定时K的取值范围;
(2)如果只采用增益校正,确定K的取值,保证闭环系统主导极点阻尼比为0.5。
(提示:采用根轨迹校正方法)
【8.5】 单位负反馈控制系统中的开环传递函数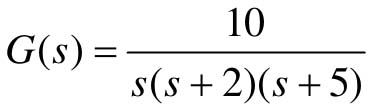 。
。
(1)利用MATLAB建立控制系统的数学模型,并绘制其根轨迹曲线,确定使系统稳定时K的取值范围;
(2)设计校正装置,保证闭环系统的主导极点位于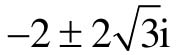 ,并且静态速度误差系数为Kv=50s-1。
,并且静态速度误差系数为Kv=50s-1。
(提示:采用根轨迹校正方法)
【8.6】 利用MATLAB中的rltool工具,重新完成习题8.5。
(提示:利用rltool工具中放置零极点位置的功能)
