4.8 综合实例及MATLAB/Simulink应用
下面通过一个综合实例,讲述MATLAB/Simulink在本章中的应用。
【例4-13】 给定RLC网络如图4.14所示。其中,ui(t)为输入量,uo(t)为输出量。求解这个系统的传递函数模型、零极点增益模型以及状态空间模型(假设R1=1Ω,R2=1Ω,C=1F,L=1H)。
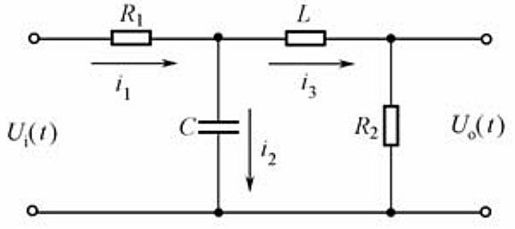
图4.14 RLC网络示意图
解:利用MATLAB求解的基本步骤如下。
【步骤1】 从数学上求出系统的传递函数。
根据电路基本定理,列出该电路的微分方程,如下:
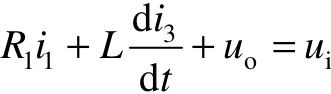
同时,该电路还满足如下关系:
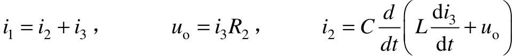
将上述三个等式代入第一个微分方程中,得到:
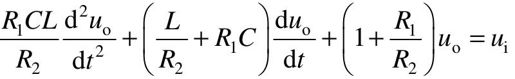
在零初始条件下,对上式取拉普拉斯变换,整理可得:
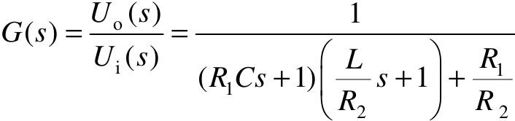
代入具体数值R1=1Ω,R2=1Ω,C=1F,L=1H,求得系统的传递函数模型:
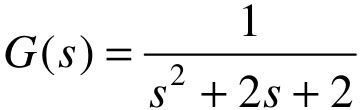
【步骤2】 使用MATLAB建立系统模型。
MATLAB程序代码如下:
- clear all; %清除工作空间的变量
- num = [0,1]; den = [1 2 2]; % 传递函数分子、分母多项式系数行向量
- sys_tf = tf( num, den ) % 建立传递函数模型
- [z,p,k] = tf2zp( num,den ) % 从传递函数模型获取系统的零极点增益
- sys_zpk = zpk( z,p,k ) % 建立系统的零极点增益模型
- [A,B,C,D] = zp2ss( z,p,k ); % 从零极点增益模型获取系统的状态空间模型
- sys_ss = ss(A,B,C,D) % 建立系统的状态空间模型
程序运行结果如下:
- Transfer function: %传递函数模型:
- 1
- -------------
- s^2 + 2 s + 2
- % 系统的零点、极点和增益:
- z = Empty matrix: 0-by-1
- p = -1.0000 + 1.0000i
- -1.0000-1.0000i
- k = 1
- Zero/pole/gain: %系统的零极点增益模型:
- 1
- ---------------
- (s^2 + 2s + 2)
- %系统的状态空间模型:
- a = x1 x2
- x1 -2 -1.414
- x2 1.414 0
- b = u1
- x1 1
- x2 0
- c = x1 x2
- y1 0 0.7071
- d = u1
- y1 0
- Continuous-time model.
【步骤3】 求取阶跃响应。
根据已经建立好的数学模型,利用MATLAB中的step函数,求解系统的阶跃响应,程序如下:
- step( sys_tf ); %求解系统的阶跃响应
- grid on; %添加栅格
输出的响应曲线如图4.15所示。
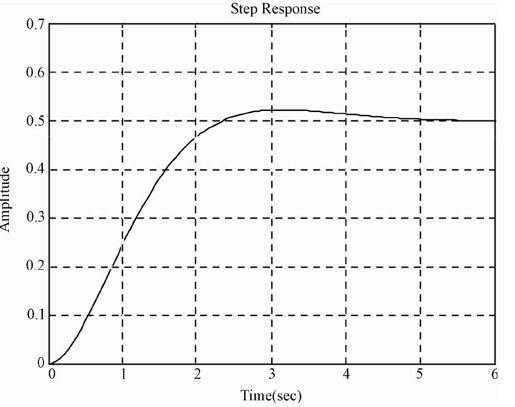
图4.15 系统的阶跃响应曲线
这是一个典型的二阶系统,后面的几章将会讨论如何利用MATLAB对系统的性能进行分析,进而研究如何对系统进行校正使系统性能达到要求。
【例4-14】 已知某双环调速的电流环系统的结构图如图4.16所示。试采用Simulink动态结构图求其线性模型。
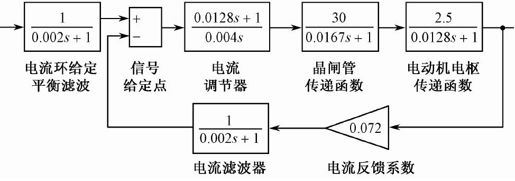
图4.16 系统结构图
解:采用Simulink动态结构图仿真的思路是:利用Simulink提供的提取线性模型的函数linmod()或linmod2(),得到状态空间模型,然后就可以对状态空间模型进行各种仿真。
【步骤1】 建立Simulink动态结构图。
按照系统结构图,在Simulink模块库中,选择相应的模块,得到如图4.17所示的该系统的动态模型,并将模型存为“Samples_4_14.mdl”文件。
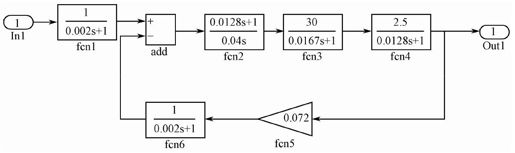
图4.17 Simulink中的系统动态模型
【步骤2】 求取系统的线性状态空间模型。
在MATLAB命令窗口中运行以下命令,得到一个线性状态空间模型(A, B, C, D),即
- [A,B,C,D]=linmod('Samples_4_14'); %提取Simulink模型的线性状态空间模型
输出结果为:
- A = 1.0e+003 *
- -0.0781 0 0 0 1.7964
- 0 -0.5000 0 0 0
- 0.0141 0 -0.5000 0 0
- 0 0.5000 -0.5000 0 0
- 0 0.1600 -0.1600 0.0250 -0.0599
- B = 0
- 1
- 0
- 0
- 0
- C = 195.3125 0 0 0 0
- D = 0
在MATLAB命令窗口中运行以下命令,得到系统的传统函数并显示出来。
- [num,den]=ss2tf(A,B,C,D); %将状态空间模型转换为传递函数模型
- printsys(num,den,'s'); %以传递函数形式显示出来
输出结果为:
- num/den =
- 9.0949e-013 s^4 + 5.8208e-010 s^3 + 56137724.5509 s^2 + 32454622005.9881 s
- + 2192879865269.466
- -------------------------------------------------------------------------------
- ------------------------
- s^5 + 1138.0052 s^4 + 392683.3832 s^3 + 43221369.7605 s^2 + 3506268712.5749 s
- + 157887350299.4013
习 题
【4.1】 控制系统结构如图4.A所示:
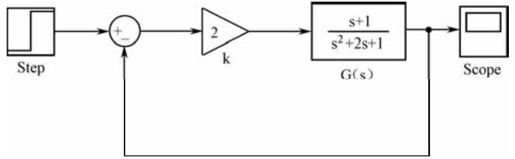
图4.A 习题
(1)利用MATLAB对以上单位负反馈控制系统建立传递函数模型;
(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
【4.2】 控制系统结构如图4.B所示:
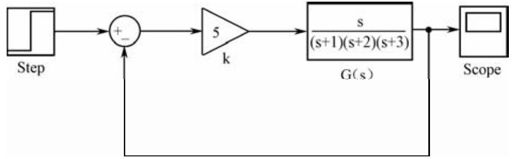
图4.B 习题
(1)利用MATLAB对图示单位负反馈控制系统建立零极点增益模型;
(2)将第一问中求得的模型转化为传递函数形式和状态空间形式。
【4.3】 控制系统的状态方程和输出方程如下:
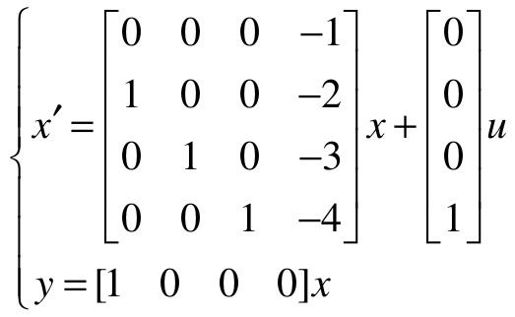
(1)利用MATLAB对控制系统建立状态空间模型;
(2)将第一问中求得的状态空间模型转化为传递函数模型和零极点增益模型。
【4.4】 某控制系统结构如图4.C所示:
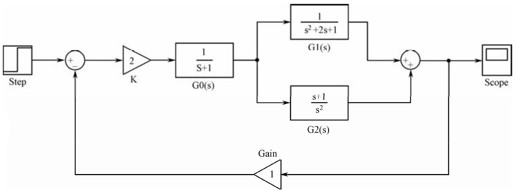
图4.C 习题
试利用MATLAB建立图示控制系统的数学模型。
【4.5】 某控制系统结构如图题4.D所示:
(1)利用MATLAB建立上述控制系统的传递函数模型;
(2)利用MATLAB得出上述控制系统的状态空间模型;
【4.6】 已知某控制系统的运动方程为y"(t)+5y'(t)+6y(t)=u(t),其中y(t)为系统输出变量,u(t)为系统的输入变量。
(1)选择一组状态变量,利用MATLAB建立系统的状态空间模型;
(2)选择另外一组状态变量,建立系统的状态空间模型;
(3)将以上两问中得到的状态空间模型转换为传递函数模型,比较结果的异同。
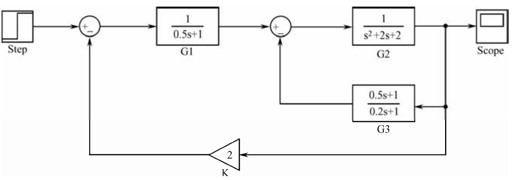
图4.D 习题
【4.7】 已知两系统的传递函数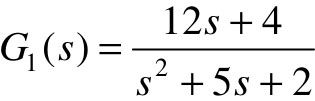 ,
,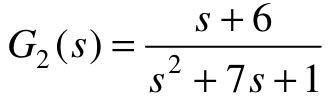 ,试分别求两系统串联、并联时的传递函数。
,试分别求两系统串联、并联时的传递函数。
【4.8】 已知单位负反馈二阶系统的开环传递函数为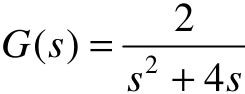 ,试利用Simulink建立系统在单位阶跃输入作用下的模型。
,试利用Simulink建立系统在单位阶跃输入作用下的模型。
