5.4 稳定性分析
自动控制系统能够正常工作的首要条件是系统必须是稳定的。稳定性的问题也是控制理论发展过程中首先涉及的一个具有实际意义的理论问题。
稳定性的提法有多种,此书仅介绍在工程中常用的经典提法。若控制系统在足够小的初始偏差作用下,其过渡过程随时间的推移逐渐衰减并趋于零,即具有恢复原平衡状态的能力,则称该系统是稳定的,否则,称该系统是不稳定的。
5.4.1 稳定性基本概念
系统稳定就是要求系统时域响应的动态分量随时间的推移而最终趋于零。设n阶线性定常系统的微分方程为:
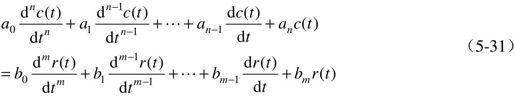
对式(5-31)进行拉氏变换,得

在式(5-32)中取R(s)=0,得到在初始状态影响下系统的时域响应(即零输入响应)为:

若pi为系统特征方程D(s)=0的根,当pi各不相同时,有:

若系统所有特征根pi的实部均为负值,即Re[pi]<0,则零输入响应(暂态响应)最终将衰减到零,即

这样的系统就是稳定的。反之,若特征根中有一个或多个根具有正实部,则暂态响应将随时间的推移而发散,即

这样的系统是不稳定的。
综上所述,系统稳定的充分必要条件是系统特征根的实部均小于零,即系统的特征根均在根平面的左半平面。
5.4.2 稳定性判据
由稳定性定义可知,稳定性问题可归结为系统闭环极点的求取,即闭环特征方程根的求取问题。由于高阶代数方程式的根一般没有解析解,故只能用数值方法来求取。其次,用直接求根法来分析系统的稳定性,不易给出系统结构和参数与稳定性的关系,对系统的综合问题帮助不大,因此需要寻求各种不直接求解代数方程式的方法来判断系统的稳定性,这就是所谓的稳定性判据。常见的稳定性判据有劳斯判据和赫尔维茨判据。
5.4.2.1 劳斯判据
设闭环特征方程式为:
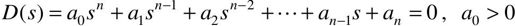
系统稳定的必要条件是:方程中各次项系数均大于0,即ai>0, i=1,2,…,n。
设n阶系统的特征方程为:
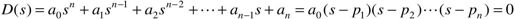
将上式的系数排成如下所示的行和列,即构成劳斯阵列(劳斯表),即
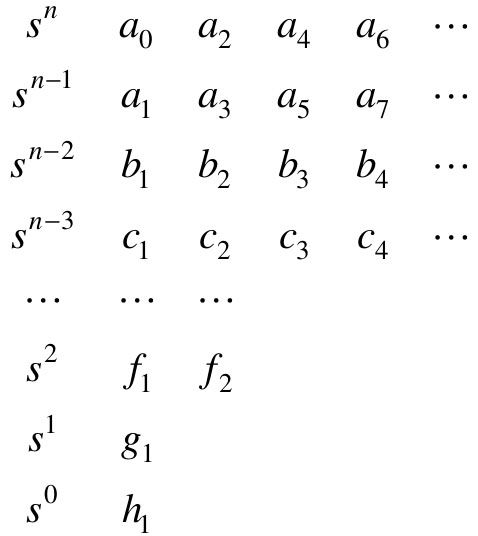
其中,
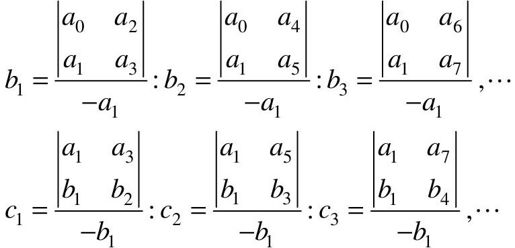
劳斯判据给出了控制系统稳定的充分条件,即劳斯表中第一列所有元素均大于零。
在使用劳斯判据时,对劳斯表计算中的一些特殊情况应引起注意:
(1)如果劳斯表中某一行的第一个元素为零,而该行其他元素并不为零,在计算下一行的第一个元素时,该元素必将趋于无穷大,以至使劳斯表的计算无法往下进行,则用一个有限小的数值ε来代替该行的第一个元素,然后按照通常方法计算。
(2)如果劳斯表中某一行的元素全部为零,表示在S平面内存在一些大小相等而符号相反的实根或共轭虚根,系统是不稳定的,则建立辅助方程式。
5.4.2.2 赫尔维茨判据
设系统的特征方程为:
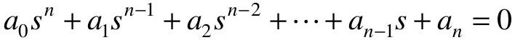
以特征方程的各项系数组成如下行列式:
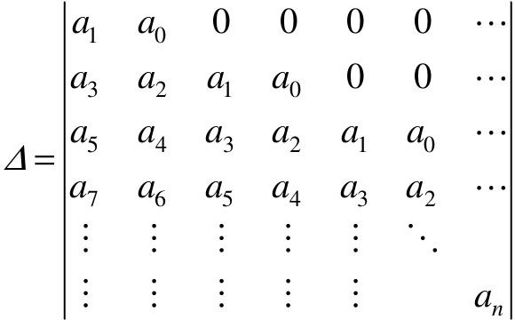
赫尔维茨判据指出,系统稳定的充分必要条件是:在a0>0情况下,上述行列式的各阶主子式Δi均大于零,即
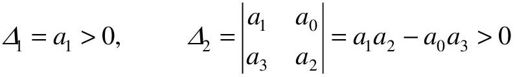
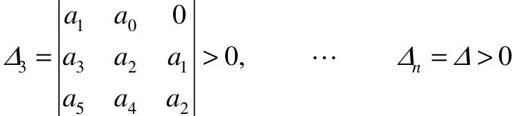
当且仅当由系统分母多项式构成的赫尔维茨矩阵为正定矩阵时,系统稳定。
5.4.2.3 稳定判据使用举例
下面通过实例来讲述稳定性判据的应用。
【例5-12】 已知系统特征方程为:s4+6s3+12s2+11s+6=0,试用劳斯判据判断其稳定性。
解:列出如下劳斯表
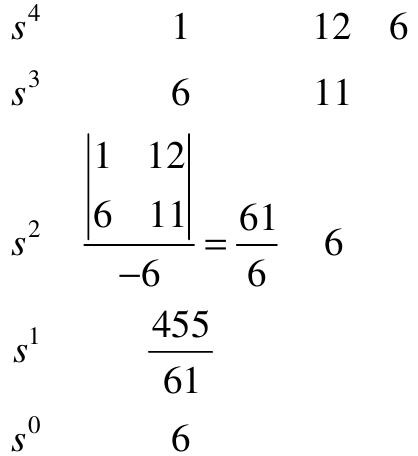
从表中可以看出,劳斯表中第一列元素大于零,因此系统是稳定的,即所有特征根均在S平面的左半平面。
【例5-13】 已知系统特征方程为:s3+10s2+16s+160=0,试用劳斯判据判断其稳定性。
解:列出如下劳斯表

劳斯表中第一列元素符号没有改变,系统没有右半平面的根,但由P(s)=0可得:
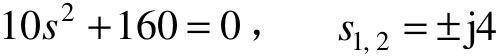
系统有一对共轭虚根,系统处于临界稳定状态,但从工程角度来看,临界稳定属于不稳定,因此该系统是不稳定的。
【例5-14】 已知系统特征方程为:s5+2s4+3s3+6s2-4s-8=0,试用劳斯判据判断其稳定性。
解:列出如下劳斯表
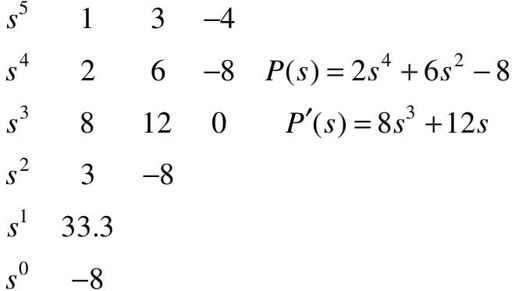
劳斯表中第一列元素符号改变一次,系统不稳定,且有一个右半平面的根,由P(s)=0得:
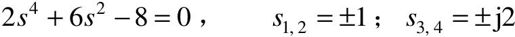
【例5-15】 已知系统特征方程为:a0s3+a1s2+a2s+a3=0,(a0>0),试用赫尔维茨判据求其稳定的充分必要条件。
解:列出如下行列式Δ:
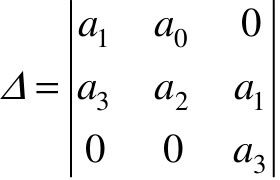
由赫尔维茨判据可知,系统稳定的充分必要条件是:
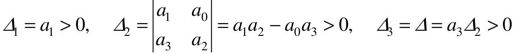
或写为:
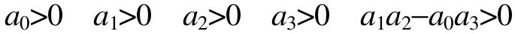
5.4.3 稳态误差分析
系统的稳态条件下输出量的期望值与稳态值之间存在的误差称为系统的稳态误差。稳态误差的大小是衡量系统稳态性能的重要指标。
5.4.3.1 稳态误差定义
考虑如图5.36所示的控制系统。
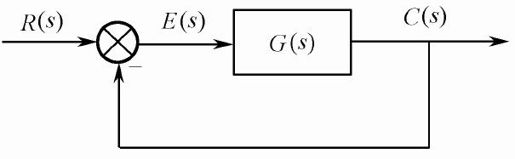
图5.36 控制系统结构示意图
其闭环传递函数为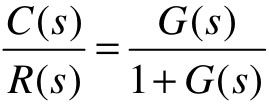 ,系统的误差e(t)一般定义为被控量的期望值与实际值之差,即
,系统的误差e(t)一般定义为被控量的期望值与实际值之差,即

则误差E(s)与输入信号R(s)之间的传递函数为:

则E(s)为:

误差响应e(t)与系统输出响应c(t)一样,也包含暂态分量和稳态分量两部分,对于一个稳定系统,暂态分量随着时间的推移将逐渐消失,需要关注的是控制系统平稳以后的误差,即系统误差响应的稳态分量(稳态误差),记为ess。
定义稳态误差为稳定系统误差响应e(t)的终值。当时间t趋于无穷时,e(t)的极限存在,则稳态误差为:
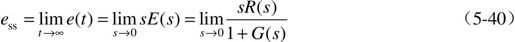
从式(5-40)可得两点结论:
- 稳态误差与系统输入信号R(s)的具体形式有关;
- 稳态误差与系统的结构和参数有关。
5.4.3.2 稳态误差系数
系统的开环传递函数G(s)H(s)可表示为:
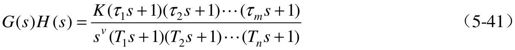
常按开环传递函数中所含有的积分环节个数来对系统进行分类。把积分环节个数为0, 1, 2,…的系统分别称为0型,Ⅰ型,Ⅱ型,…系统。
下面看一下几种常见的稳态误差系数,即静态位置误差系数Kp、静态速度误差系数Kv和静态加速度误差系数Ka。
- 静态位置误差系数Kp
当系统的输入为单位阶跃信号r(t)=1(t)时,由式(5-40)有
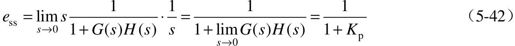
式中,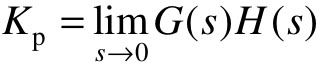 ,定义为系统静态位置误差系数。
,定义为系统静态位置误差系数。
对于0型系统,有
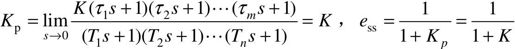
对于Ⅰ型或Ⅰ型以上系统,有
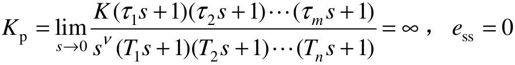
- 静态速度误差系数Kv
当系统的输入为单位斜坡信号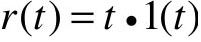 时,
时, ,由式(5-40)有
,由式(5-40)有
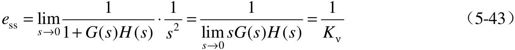
式中,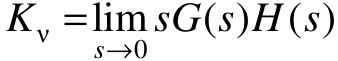 ,定义为系统静态速度误差系数。
,定义为系统静态速度误差系数。
对于0型系统,有
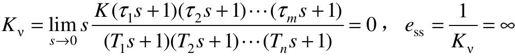
对于Ⅰ型系统,有
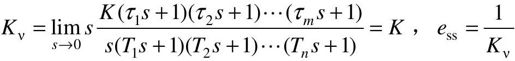
对于Ⅱ型或Ⅱ型以上系统,有
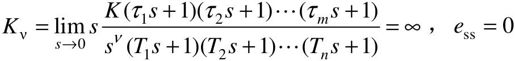
- 静态加速度误差系数Ka
当系统输入为单位加速度信号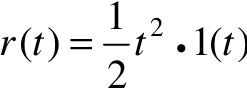 时,
时,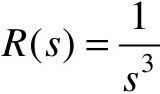 ,则系统稳态误差为:
,则系统稳态误差为:

式中, ,定义为系统静态加速度误差系数。
,定义为系统静态加速度误差系数。
对于0型系统,有Ka=0, ess=∞。
对于Ⅰ型系统,有Ka=0, ess=∞。
对于Ⅱ型系统,有Ka=K。
对于Ⅲ型或Ⅲ型以上系统,有Ka=∞, ess=0。
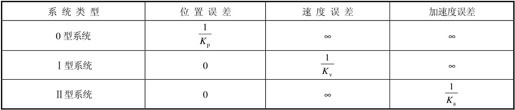
几种常见系统的稳态误差如表5.1所示。
表5.1 几种常见系统的稳态误差
【例5-16】 已知单位负反馈控制系统,其中开环传递函数为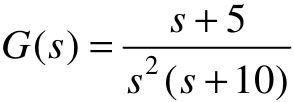 ,试计算当输入为单位阶跃信号、单位斜坡信号和单位加速度信号时系统的稳态误差。
,试计算当输入为单位阶跃信号、单位斜坡信号和单位加速度信号时系统的稳态误差。
解:Simulink的模型如图5.37所示。
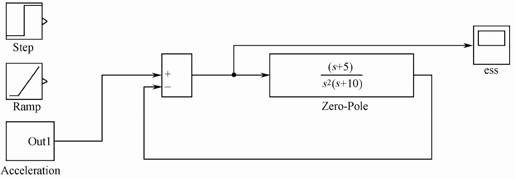
图5.37 例5-16的Simulink模型
图中,“Zero-Pole”建立G(s)的模型,信号源选择“Step”(单位阶跃信号)、“Ramp”(单位斜坡信号)和使用基本模块构成的“Acceleration”(单位加速度信号),“Acceleration”的子系统如图5.38所示,它由单位斜坡信号和y=0.5u2(u为输入信号,y为输出信号)的函数串联而成。
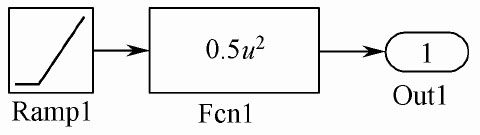
图5.38 例5-16的Acceleration子系统模型
信号源选定“Step”时,连好模型进行仿真,仿真结束后,双击示波器,输出图形如图5.39所示,它是输入信号为单位阶跃时系统的输出误差。
信号源选定“Ramp”时,连好模型,进行仿真,仿真结束后,双击示波器,输出图形如图5.40所示,它是输入信号为单位斜坡时系统的输出误差。
信号源选定“Acceleration”时,连好模型,进行仿真,仿真结束后,双击示波器,输出图形如图5.41所示,它是输入信号为单位加速度时系统的输出误差。
从图5.39、图5.40、图5.41可以看出不同输入情况下系统的稳态误差,系统是II型系统,因此在阶跃、斜坡输入信号下,系统的稳态误差都为零,在加速度信号输入下,存在稳态误差,稳态误差的数值通过放大示波器可以准确地看到,数值为2,而且仿真时间越长,离2就越接近,这与通过稳态误差系数计算的结果吻合。
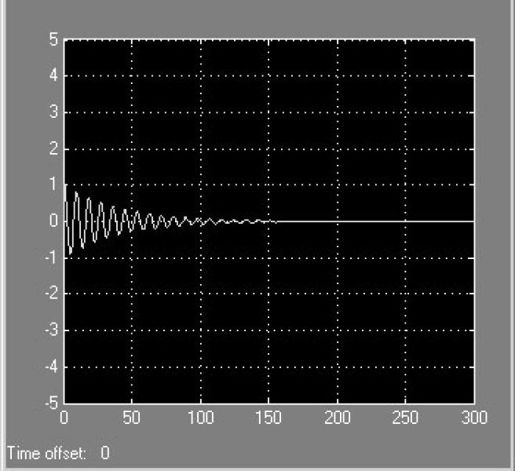
图5.39 单位阶跃时系统的输出误差
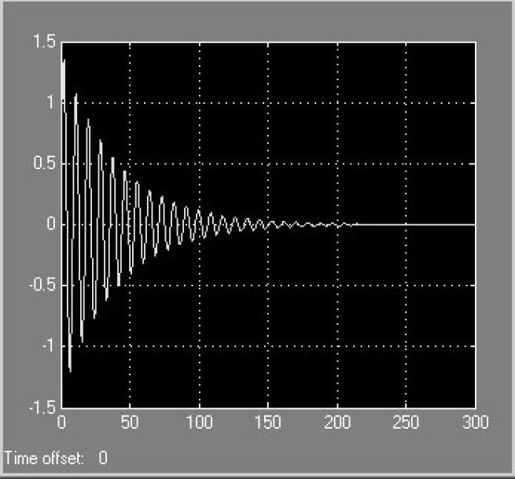
图5.40 单位斜坡时系统的输出误差
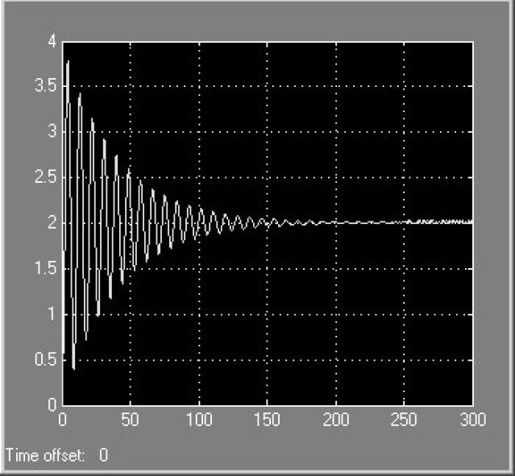
图5.41 单位加速度时系统的输出误差
5.4.4 MATLAB在稳定性分析中的应用
MATLAB提供了直接求取系统所有零极点的函数,因此可以直接根据零极点的分布情况对系统的稳定性进行判断。
MATLAB提供了直接求根的命令roots,因此可以用直接求根来判断稳定性,至于稳定范围的求取,则可以用循环语句迭代计算的方法来求取。下面给出应用实例。
【例5-17】 已知单位负反馈控制系统的开环传递函数为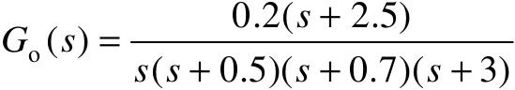 ,试用MATLAB编写程序判断此闭环系统的稳定性,并绘制闭环系统的零极点图。
,试用MATLAB编写程序判断此闭环系统的稳定性,并绘制闭环系统的零极点图。
解:MATLAB程序代码如下。
- z=-2.5; p=[0, -0.5, -0.7, -3]; k=0.2 %开环零点、极点、增益
- Go=zpk(z, p, k) %建立零极点形式的开环传递函数
- Gc=feedback(Go, 1) %单位负反馈连接
- Gctf=tf(Gc) %建立闭环传递函数
- dc=Gctf.den %获取闭环传递函数的特征多项式
- dens=poly2str(dc{1}, 's') %将特征多项式系数转换为字符形式的函数,便于查看
运行结果如下:
- dens = s^4 + 4.2 s^3 + 3.95 s^2 + 1.25 s + 0.5
dens是系统的特征多项式,接着输入如下MATLAB程序代码:
- den =[1, 4.2, 3.95, 1.25, 0.5] %提取其多项式系数
- p=roots(den) %求取特征根
运行后,输出特征根p如下:
- p =-3.0058
- -1.0000
- -0.0971 + 0.3961i
- -0.0971 - 0.3961i
可见,系统只有负实部的特征根,因此闭环系统是稳定的。
下面绘制系统的零极点图,在命令窗口接着输入以下MATLAB程序代码:
- pzmap(Gctf) %绘制零极点图
- grid %添加栅格
运行程序,输出如图5.42所示,其中闭环极点用“×”标识,闭环零点用“O”标识。
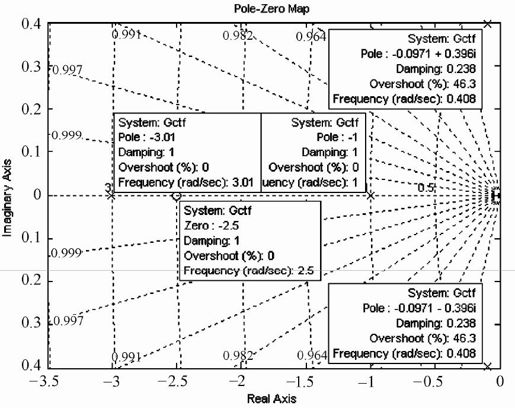
图5.42 例5-17闭环零极点图
