6.5 用根轨迹法分析系统的暂态特性
前几节讨论了如何根据开环系统的传递函数求取闭环系统的根轨迹。根轨迹求出后,对于一定的增益K值,就可利用幅值条件,确定系统的特征根(闭环极点)。如果闭环系统的零点、输入信号是已知的,那么可以结合根轨迹,在图上直观地对系统的暂态特性展开分析。用根轨迹法分析系统暂态品质的最大优点是:可以看出在开环放大系数发生变化时,系统的暂态品质是怎样变化的。
从前面章节可得出以下基本结论:
(1)如果已知系统的闭环零极点分布,那么控制系统的动力学性能就可唯一确定。在给出具体输入函数的条件下,可以求出其输出响应和性能指标。
(2)如果所有闭环极点均分布于复平面虚轴左侧,那么系统是稳定的。
(3)稳定系统的动力学特性主要取决于主导极点的位置。所谓主导极点指的是它们距虚轴的距离较其他闭环零极点距虚轴的距离近5倍或5倍以上。
(4)其他闭环零极点对系统动力学性能的影响:在主导极点的基础上,增加闭环极点,系统的响应速度将降低而超调量将减少;闭环零点的作用则刚好相反,其影响程度将随着距虚轴距离的减小而增强。
(5)偶极子对系统动力学性能的影响可以忽略。所谓偶极子指的是一对靠近的闭环零极点,它们之间的距离较它们本身到虚轴的距离要小10倍或10倍以上。
由上可知,可以由闭环零极点的分布来分析系统的时域响应。从前面的分析可知,闭环零点是开环传递函数中G(s)的零点和H(s)的极点,可以从开环传递函数中直接得到;而闭环极点,可以在根轨迹图上求出,例如利用MATLAB的rlocfind( )函数可以很方便、直观地求出系统的闭环极点。
【例6-9】 绘制以下系统的根轨迹并利用根轨迹图分析系统性能。已知一个三阶系统的开环传递函数为 ,试从根轨迹图分析其单位负反馈系统的暂态特性。
,试从根轨迹图分析其单位负反馈系统的暂态特性。
解:MATLAB程序代码如下。
- num=1; den=conv([1, 0], conv( [1, 1], [1, 4]) );
- %传递函数分子、分母多项式系数行向量
- sys=tf(num, den) %建立传递函数模型
- rlocus(sys); grid on; %绘制根轨迹图并添加栅格
- [k, poles]=rlocfind(sys) %计算用户所选定的点处的增益和其他闭环极点
- title('根轨迹图') %添加图标题
运行程序,输出如图6.16所示的根轨迹图,图中,“×”表示闭环系统的极点,“○”表示闭环系统的零点。由于根轨迹所绘制的范围很大,显示出来的部分看得不是非常仔细,因此需要结合工具栏上的放大、缩小和拖拉等工具,方便灵活地查看根轨迹。如果用鼠标单击图中的曲线,可以得到一个文本框,里面显示对应的系统名(System)、增益(Gain)、极点(Pole)、阻尼比(Damping)、超调(Overshoot)、角频率(Frequency)等参数。
从图6.16可以看出,在根轨迹上选定的那点的参数:增益为8.37、极点为0.209±j2.48、阻尼比为-0.0839、超调为130%、角频率为2.49rad/s,从这些参数可以看出,此时系统是不稳定的。同时,此时的根轨迹上的那点位于虚轴的左半平面。
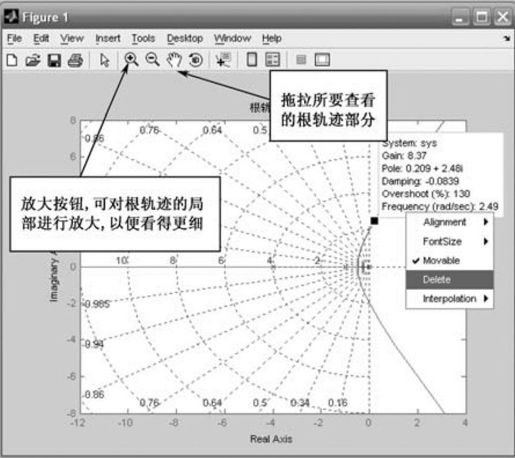
图6.16 例6-9的根轨迹图
非常方便的是,显示上述参数的文本框有一些属性,如可移动性(Movable),当选中Movable后,便可以方便地找到所需要看到的根轨迹上的点。
还可求得当K≈0.22时,闭环系统的两个极点重合在实轴上,输出结果如图6.17所示,极点以“+”表示。
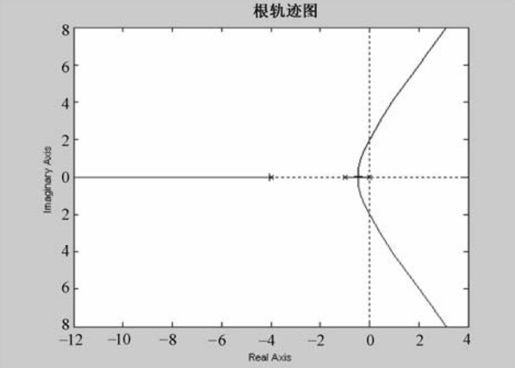
图6.17 例6-9的根轨迹图2
进一步减小K值,会看到其中一个极点将沿实轴向原点靠拢,如图6-18所示,暂态响应越来越慢。如果K=0.75,此时一对复极点(p1, p2=-0.39±j0.745)的实部比另一个极点(p3=-4.22)的实部大得多,因此完全可以忽略p3的影响,这样就可以用二阶系统的指标来分析系统的暂态特性。
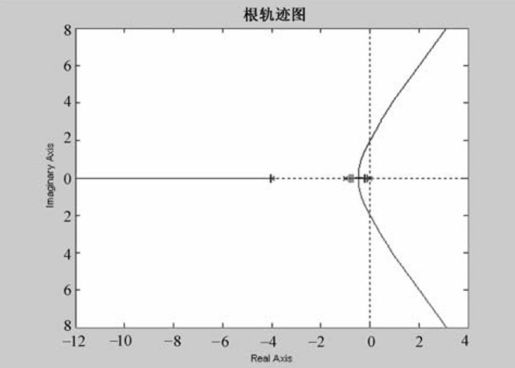
图6.18 例6-9的根轨迹图3
系统的动态性能最终体现在时间响应上,影响时间响应的因素有两个:闭环传递函数和输入函数。从前面的分析可知:时间响应的暂态分量主要取决于闭环零点和极点,时间响应的稳态分量主要取决于输入函数。
闭环系统的稳定性完全取决于闭环极点,实际上时间响应的暂态分量也主要取决于闭环极点。每一个闭环极点pi在S平面上的位置决定了它对应的暂态分量的运动形式。
图6.19表示了pi分布于S平面上不同位置所对应的暂态分量,其规律可以总结为:
(1)左右分布决定终值。pi位于虚轴左边时暂态分量最终衰减到零,pi位于虚轴右边时暂态分量一定发散,pi正好位于虚轴(除原点)时暂态分量为等幅振荡。
(2)虚实分布决定振型。pi位于实轴上时暂态分量为非周期运动,pi位于虚轴上时暂态分量为周期运动。
(3)远近分布决定快慢。pi位于虚轴左边时,离虚轴越远过渡过程衰减得越快。所以离虚轴最近的闭环极点“主宰”系统响应的时间最长,是主导极点。
系统的闭环零点对系统的稳定性没有影响,对系统的时间响应没有实质影响,但对时间响应的具体形状是有影响的。
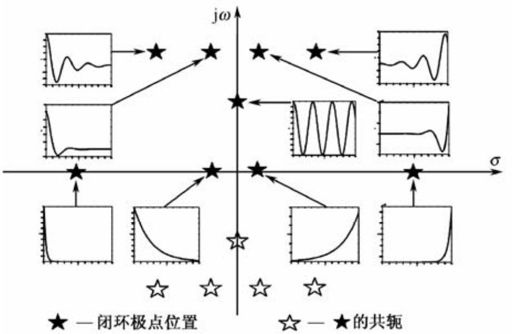
图6.19 闭环极点分布与暂态分量的运动形式
