12.6　离散控制系统性能分析

12.6.1　稳定性分析

在线性连续系统中，根据特征方程的根在S平面的位置判别系统的稳定性。若系统特征方程的所有根都在S平面左半平面，则系统稳定。对线性离散系统进行了Z变换以后，对系统的分析要采用Z平面，因此需要弄清这两个复平面之间的相互关系。

  1. S平面到Z平面的映射关系

S平面到Z平面的映射关系式为z=eTs，其中，s是复变量，也可写成s=σ+jω，所以z也是复变量，即z=eTs=eTσejωT。

极坐标形式为：z=|z|ejθ，其中，|z|=eTσ，θ=ωT。

因此，从上式的关系可得到Z平面的稳定条件，如表12.9所示。

表12.9　Z平面稳定条件

P_355-1

由此可见，S平面的左半平面对应于Z平面以原点为圆心的单位圆内，S平面的虚轴映射为Z平面的单位圆边界，如果12.15所示。

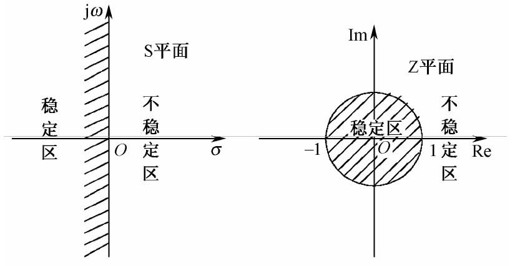
P_355-2

图12.15　S平面和Z平面的稳定区域

应当指出，如同分析连续系统的稳定性一样，用解特征方程根的方法来判别高阶采样系统的稳定性是很不方便的。因此，需要采用一些比较实用的判别系统稳定性的方法，其中比较常用的代数判据是劳斯判据。

  1. 离散控制系统稳定性判据

离散控制系统闭环稳定的充分条件是：闭环脉冲传递函数的全部极点均位于单位圆内。因此判断离散控制系统稳定性的最直接的方法是计算闭环特征方程的根，然后根据根的位置来确定系统的绝对稳定性。

劳斯判据是判断连续系统是否稳定的一种简单的代数判据。由于连续系统和离散系统的稳定区不同，所以在离散控制系统中不能直接应用劳斯判据，必须进行变换。基于双线性变换和劳斯判据的方法能用来判断离散控制系统的稳定性。

该方法是将离散控制系统用双线性变换将Z平面单位圆内的点映射到W平面的左半平面，然后用劳斯判据判别系统的稳定性。

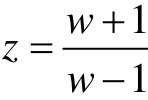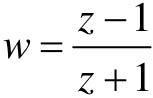复变函数双线性变换公式为：H_355-0-1，其中w是复变量，可写成：w=σw+jωw，或H_355-0-2。

这样，Z平面单位圆内部就变换到W平面的左半平面，它可以从几何上和数学上加以证明，此处从略。

因此稳定的条件就变为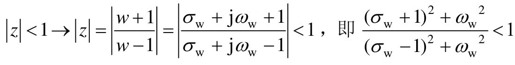：H_355-01。化简得：σw<0。

12.6.2　静态误差分析

在离散控制系统中，稳态误差系数的计算和线性连续系统中的类似，下面以单位反馈采样系统为例介绍系统的稳态误差系数。

设单位反馈采样系统如图12.16所示，其开环脉冲传递函数为G(z)。

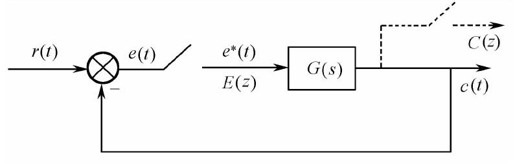
P_356-1

图12.16　单位反馈采样系统

采样系统的稳态误差既可从输出信号在各采样时刻的数值c(nT)(n=0,1,2,…,∞)中得到，也可以从过渡过程曲线c*(t)中求取，还可以应用Z变换的终值定理来计算。

系统的闭环传递函数Y(z)=Φ(z)R(z)，其中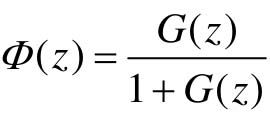H_356-01。

系统误差如下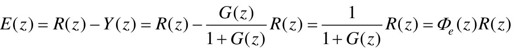：H_356-02。

利用Z变换的终值定理求的瞬时稳态误差为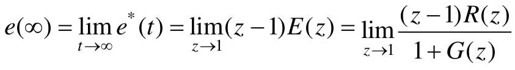：H_356-03，可以看出，系统的稳态误差e(∞)与G(z)及输入信号的形式有关。

由于z=eTs，原线性连续系统开环传递函数G(s)在s=0处极点的个数v作为划分系统型别的标准，可推广为将离散系统开环脉冲传递函数G(z)在z=1处极点的数目v作为离散系统的型别，将v=0, 1, 2的系统分别称为0型、I型、II型离散系统。

下面是几种典型输入条件下的稳态误差。

  1. 单位阶跃输入时的稳态误差

把单位阶跃函数的Z变换式代入e(∞)的表达式，得到单位阶跃输入时的稳态误差为

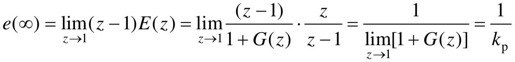
P_356-2

式中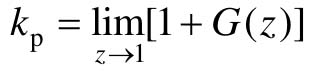，H_356-05，称为静态位置误差系数。

对0型离散系统（没有z=1的极点），kp≠∞，从而e(∞)≠0；对I型、II型以上的离散系统（有一个或一个以上z=1的极点），kp=∞，从而e(∞)=0。

因此，在单位阶跃函数作用下，0型离散系统在采样瞬时存在位置误差；I型或II型以上的离散系统在采样瞬时没有位置误差。这与连续系统十分相似。

  1. 单位斜坡输入时的稳态误差

把单位阶跃函数的Z变换式代入式（12-69），得到单位阶跃输入时的稳态误差为

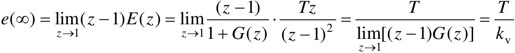
P_356-3

式中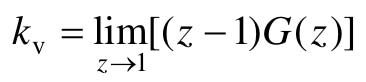，H_357-01，称为静态速度误差系数。

因为0型系统的kv=0，I型系统的为有限值，II型和II型以上系统的为无限值，所以有如下结论：0型离散系统不能承受单位斜坡函数作用；I型离散系统在单位斜坡函数作用下存在速度误差；II型和II型以上离散系统在单位斜坡函数作用下不存在稳态误差。

  1. 单位加速度输入时的稳态误差

把单位阶跃函数的Z变换式代入e(∞)的表达式，得到单位阶跃输入时的稳态误差为：

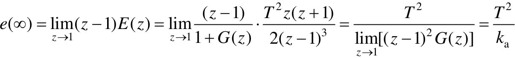
P_357-1

式中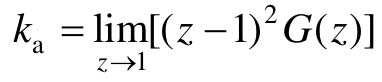，H_357-02，称为静态加速度误差系数，当然，上式也是系统的稳态位置误差，因此也称为加速度误差。

由于0型及I型系统的Ka=0，II型系统的为常值，III型及III型以上系统的Ka=∞，因此有如下结论：0型及I型离散系统不能承受单位加速度函数作用；II型离散系统在单位加速度函数作用于下存在加速度误差；只有III型及III型以上的离散系统在单位加速度函数作用下才不存在采样瞬时的稳态位置误差。

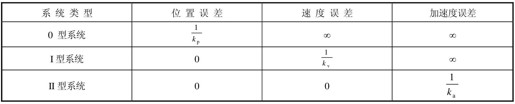
三种类型系统的误差系数归结如表12.10所示。

表12.10　三种类型系统的误差系数表

P_357-2

12.6.3　动态特性分析

在线性连续系统中，闭环传递函数零、极点在S平面的分布对系统的暂态响应有非常大的影响。与此类似，采样系统的暂态响应与闭环脉冲传递函数零、极点在Z平面的分布也有密切的关系。

设闭环系统的脉冲传递函数为

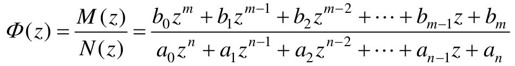
P_357-3

式中，m<n。为便于分析，设其无重极点（极点分别为p1, p2, …, pn）。

采样系统的单位阶跃响应为：y(z)=Φ(z)R(z)，其中R(z)=z/(z-1)，则Y(z)可写成

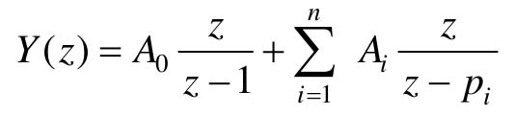
P_357-4

式中，Ai为留数，通过Z反变换导出输出信号的脉冲序列y*(t)在技术上并无困难。

可求得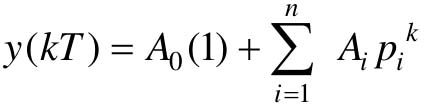H_357-03，式中，第一项为系统输出的稳态分量，第二项为输出的暂态分量。显然，随着极点在Z平面位置的变化，它所对应的暂态分量也不同。

  1. 实轴上有闭环单极点

设闭环极点pi为正实数，pi对应的暂态项为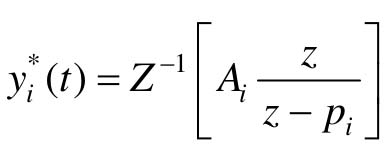H_358-01：

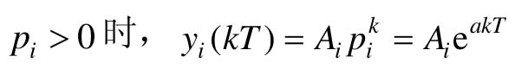  • H_358-02，动态过程为按指数规律变化脉冲序列；
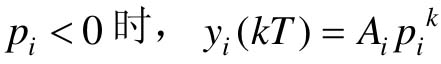  • H_358-03，动态过程为交替变号的双向脉冲序列。

闭环实极点分布与相应动态响应形式的关系，如图12.17所示。

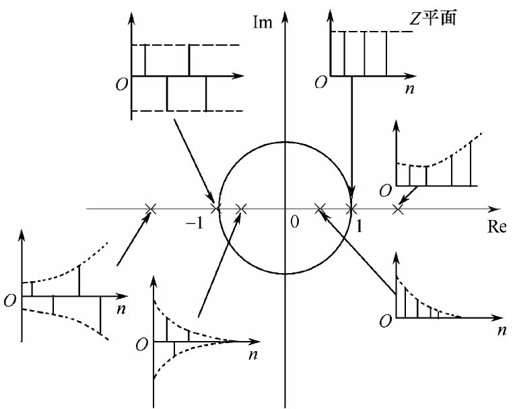
P_358-1

图12.17　实极点与动态响应的关系

从图12.17中可以看出：

  • 当闭环实数极点位于右半Z平面，则输出动态响应形式为单向正脉冲序列。实极点位于单位圆内，脉冲序列收敛，且实极点越接近原点，收敛越快；实极点位于单位圆上，脉冲序列等幅变化；实极点位于单位圆外，脉冲序列发散。
  • 若闭环实数极点为于左半Z平面，则输出动态响应形式为双向交替脉冲序列。实极点位于单位圆内，双向脉冲序列收敛；实极点位于单位圆上，双向脉冲序列等幅变化；实极点位于单位圆外，双向脉冲序列发散。
  1. 闭环共轭复极点

P_358-2

若|ph|>1，则闭环复数极点位于Z平面上的单位圆外，动态响应为振荡脉冲序列。

若|ph|=1，则闭环复数极点位于Z平面上的单位圆上，动态响应为等幅振荡脉冲序列。

若|ph|<1，则闭环复数极点位于Z平面上的单位圆内，动态响应为振荡收敛脉冲序列，且模越小，即复极点越靠近原点，振荡收敛越快。

闭环复数极点分布与相应动态响应形式的关系，如图12.18所示。

从图12.18中可以看出，闭环脉冲传递函数的极点在Z平面上的位置决定相应暂态分量的性质和特点。

  • 当闭环极点位于单位圆内时，其对应的暂态分量是衰减的，极点离原点越近衰减越快；
  • 当闭环极点位于正实轴上时，暂态分量按指数衰减，一对共扼复数极点的暂态分量为振荡衰减，其角频率为θk/T；
  • 当闭环极点位于负实轴上时，暂态分量也出现衰减振荡，其振荡角频率为π/T。

因此，为了使采样系统具有较为满意的暂态响应，其z传递函数的极点最好分布在单位圆内的右半部靠近原点的位置。在线性连续系统中采用的，根据一对主导极点分析系统暂态响应的方法，也可以推广到采样系统。

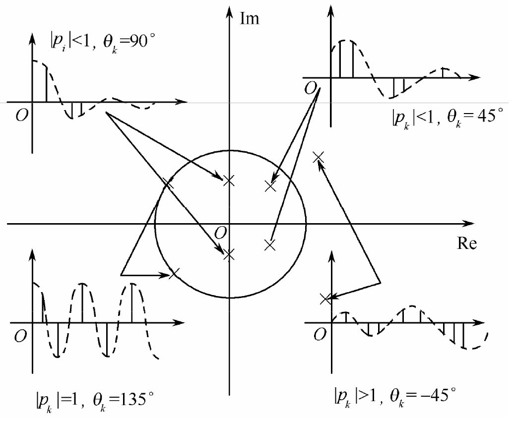
P_359-1

图12.18　复极点分布与响应的关系

12.6.4　MATLAB/Simulink在离散系统性能分析中的应用

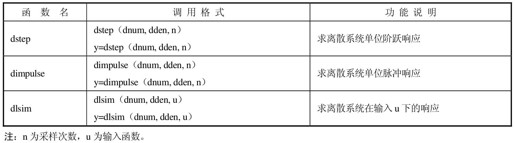
在MATLAB中，提供了用于求离散系统时域响应和频域响应的函数，分别如表12.11和表12.12所示。

表12.11　离散系统时域响应函数

P_359-2

离散时间LTI系统频域分析方法主要有3种：Bode图（开环对数幅频/相频特性曲线）法、Nyquist曲线（开环频率特性G(jω)的极坐标图）法和Nichols图（开环对数幅相图）法。表12.12列出了离散系统的频域分析函数。

表12.12　离散系统频域响应函数

P_360-1

下面通过几个实例，具体讲述MATLAB/Simulink在离散系统性能分析中的应用。

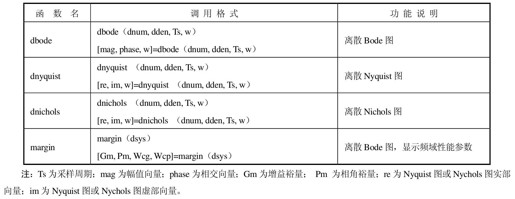
【例12-4】　已知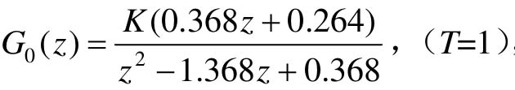H_360-01，试用劳斯判据确定离散系统稳定的K值范围。

解：首先进行w变换，代入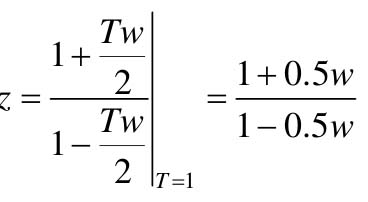H_360-02，得

P_360-2

由1+G0(w)=0导出特征方程式为

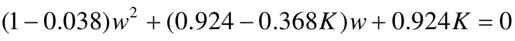
P_360-3

列出劳斯表，可以求出离散系统稳定的K值范围为0<K<2.394。

【例12-5】　使用MATLAB画出离散系统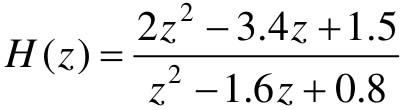H_360-03的带栅格线的根轨迹图。

解：MATLAB程序代码如下。

  1. num=[2, -3.4, 1.5]; den=[1, -1.6, 0.8];    %传递函数分子、分母多项式系数行向量
  2. axis('equal')      %对两个轴用统一的比例尺度
  3. zgrid('new')      %绘制出由等阻尼系数与自然振荡角频率组成的栅格线
  4. rlocus(num, den)        %绘制根轨迹图
  5. title('带栅格线的离散系统的根轨迹图')  %添加图标题

程序运行后得到如图12.19所示的根轨迹图。

【例12-6】　给定系统闭环传递函数为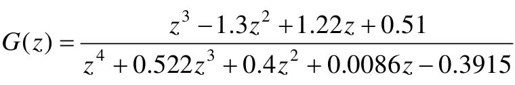H_360-04，（T=0.5），试绘制其零极点图，并判断此系统的稳定性。

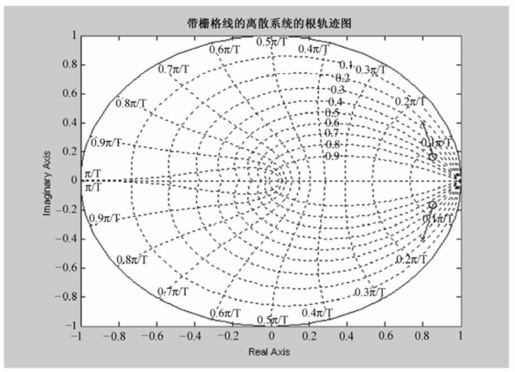
P_361-1

图12.19　例12-5带栅格线的离散系统根轨迹

解：MATLAB程序代码如下。

  1. num=[1 -1.3 1.22 0.51]; den=[1 0.522 0.4 0.0086 -0.3915];
  2. G=tf(num,den,0.5);
  3. pzmap(G);
  4. axis([-1.2 1.2 -1.2 1.2]);
  5. axis equal;

程序运行后得到如图12.20所示的根轨迹图。

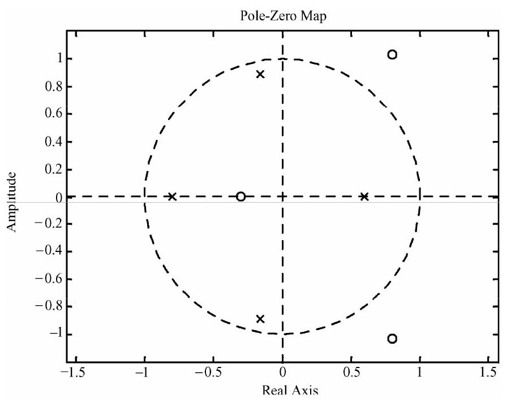
P_361-2

图12.20　例12-6的离散系统根轨迹

从根轨迹图上可以看出，闭环传递函数的所有极点都在单位圆内部，闭环系统稳定。

【例12-7】　设采样控制系统的开环脉冲传递函数为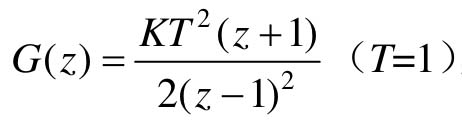：H_361-01，试用根轨迹方法说明，对任意K闭环系统都是不稳定的。

解：MATLAB程序代码如下。

  1. num=[1 1]; den=2*conv([1 -1], [1 -1]);
  2. G=tf(num,den,1);
  3. rlocus(G)
  4. axis equal;

程序运行后得到如图12.21所示的根轨迹图。

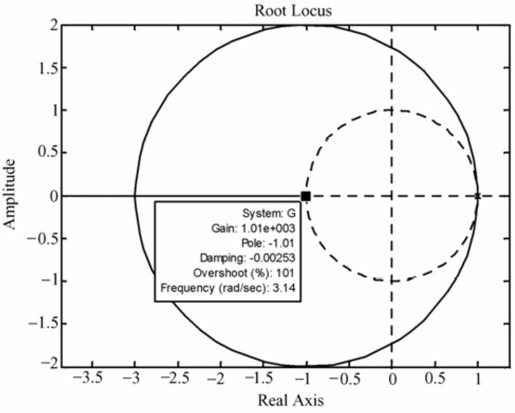
P_362-1

图12.21　例12-7的离散系统根轨迹

由系统根轨迹图可知，根轨迹并不穿过Z平面的单位圆区域，即所有的闭环极点都在单位圆外，此闭环系统始终不稳定

【例12-8】　已知一个离散线性系统如图12.22所示，其中采样周期Ts=1s，对象模型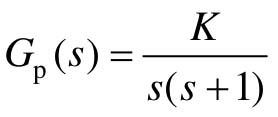H_362-01，零阶保持器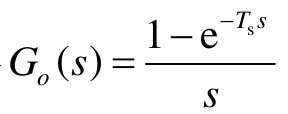H_362-02，试求开环增益的稳定范围。

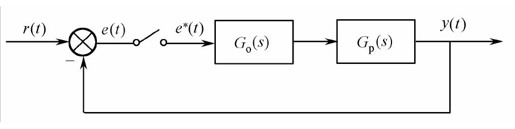
P_362-2

图12.22　离散系统结构图

解：开环系统的传递函数

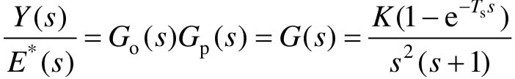
P_362-3

对开环传递函数进行Z变换，并将Ts=1s代入，得：

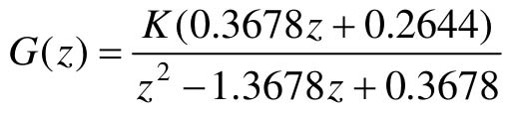
P_362-4

闭环Z传递函数T(z)的极点是特征方程q(z)=[1+G(z)]=0的根，因此

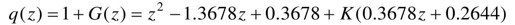
P_362-5

MATLAB程序代码如下：

  1. num=[0.3678, 0.2644];  den=[1, -1.3678, 0.3678];  sys=tf(num, den, -1)
  2. rlocus(sys)        %绘制根轨迹
  3. [k, poles]=rlocfind(sys)      %选择根轨迹上的点

用鼠标单击根轨迹与单位圆的交点，输出如下：

  1. Transfer function:
  2.   0.3678 z + 0.2644
  3. ----------------------
  4. z^2 - 1.368 z + 0.3678
  5. Sampling time: unspecified
  6. Select a point in the graphics window
  7. selected_point=   0.2494 + 0.9736i
  8. k=    2.3874
  9. poles=   0.2449 + 0.9691i
  10.          0.2449 - 0.9691i
  11. >> abs(poles)       %计算极点的模
  12. ans=    0.9995
  13.          0.9995

从输出结果可近似得到临界稳定的根轨迹图，根据根轨迹图可得系统稳定的K值范围。输出的根轨迹如图12.23所示。

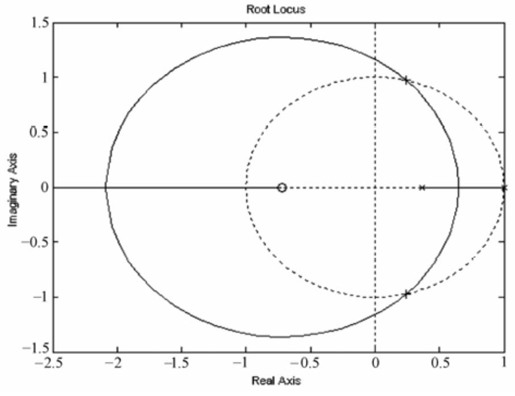
P_363-1

图12.23　根轨迹图

在离散系统根轨迹图上，虚线表示的是单位圆，从根轨迹的走向以及与单位圆的交点可以大致判断系统的稳定性。

本例中，一个极点位于单位圆上，另一个位于单位圆中，因此，系统在K=0时是稳定的；随着K值的增大，两条根轨迹离开单位圆，系统变得不稳定；随着K值继续增大，虽然有一个极点落在单位圆内，但另一个极点趋向实轴的无穷远处，系统是不稳定的。所以K值的稳定范围是从0开始的一段区间。从图12.23上可以看出，使系统稳定的K值的稳定范围略为0<K<2.39。

【例12-9】　已知一个离散线性系统如图12.24所示，对象模型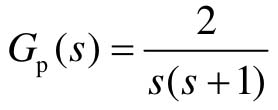H_363-01，Go(s)为保持器，R(t)为单位阶跃输入，试求：

（1）当Go(s)为零阶保持器时，采样周期Ts=0.1s, 1s, 2s时系统的输出。

（2）当采样周期Ts=1s时，保持器为零阶保持器和一阶保持器时系统的输出。

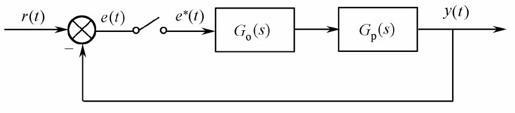
P_364-1

图12.24　离散系统结构图

解：此题可利用Simulink中的模型离散化工具Model Discretizer来实现系统在不同采样周期条件下的响应，其操作步骤如下。

（1）打开Simulink，建立系统系统模型，如图12.25所示。

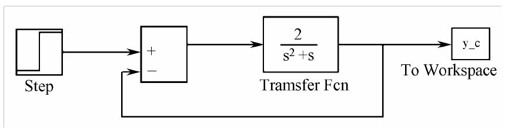
P_364-2

图12.25　例12-9连续系统的Simulink仿真图

（2）选择Model Discretizer工具，其路径是Tools→Control Design→Model Discretizer，如图12.26所示。

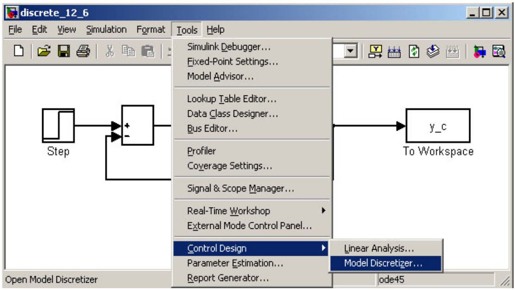
P_364-3

图12.26　进入Model Discretizer的菜单

（3）打开Model Discretizer工具，如图12.27所示。在Transform method的下拉选项中选定Z变换的方法，这些方法有'zoh'、'foh'、'imp'、'tustin'、'prewarp'和'matched'，它们的含义在前面已做介绍；在Sample time中输入采样周期；在Replace current selection with的下拉选项中选定变换后的模型参数显示，显示的方式有Discrete blocks （Enter parameters in s-domain）（模型框显示原连续系统的参数）、Discrete blocks （Enter parameters in z-domain）（模型框显示变换后的离散系统的参数）、Configurable subsystem （Enter parameters in s-domain）（子系统显示原连续系统的参数）和Configurable subsystem （Enter parameters in z-domain）（子系统显示变换后的离散系统的参数）；最后单击图标H_364-0-1实现模型的转换，变换后的模型如图12.28所示。

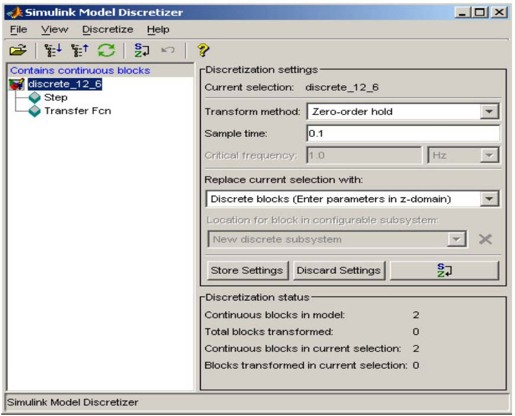
P_365-1

图12.27　Model Discretizer界面

P_365-2

图12.28　例12-9连续系统变换后的离散系统仿真图

在本例中，依次按照上述步骤进行模型转换，可方便地求得不同变换条件下系统的输出。

（4）在Transform method的下拉选项中选定'zoh'，在Sample time中输入0.1，在Replace current selection with的下拉选项中选定Discrete blocks （Enter parameters in z-domain）进行转换后并仿真，系统输出如图12.29所示。它是系统采用零阶保持器时，采样周期Ts=0.1s离散s后的系统输出。

用类似的方法得到系统采用零阶保持器时，采样周期Ts=1s离散后的系统输出，如图12.30所示。

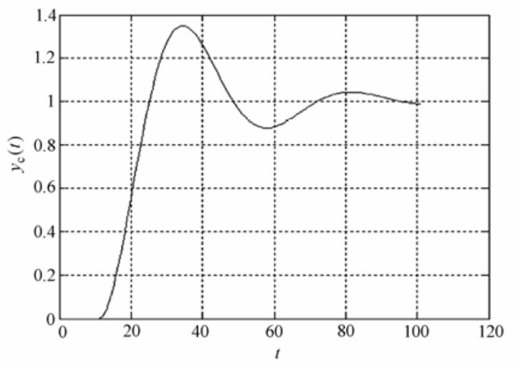
P_365-3

图12.29　采用零阶保持器时，采样周期Ts=0.1s离散后的系统输出

P_366-1

图12.30　采用零阶保持器时，采样周期Ts=1s离散后的系统输出

当系统采用零阶保持器时，采样周期Ts=2s离散后的系统的输出如图12.31所示。

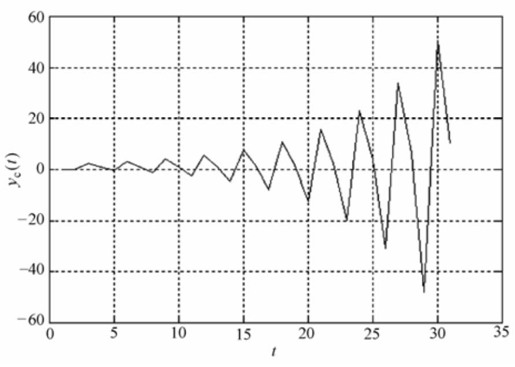
P_366-2

图12.31　采用零阶保持器时，采样周期Ts=2s离散后的系统输出

当系统采用一阶保持器时，采样周期Ts=1s离散后的系统输出如图12.32所示。

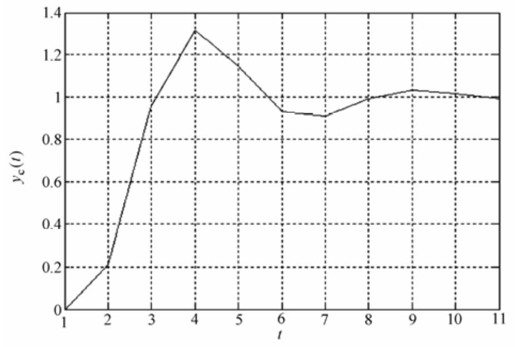
P_366-3

图12.32　采用一阶保持器时，采样周期Ts=1s离散后的系统输出

从以上结果可以看出，在同样的保持器下，随着采样周期的增大，系统稳定性能变差；而在同一采样周期条件下，采用一阶保持器变换的系统的动态特性比采用零阶保持器变换的系统要好。

【例12-10】　若某控制系统结构如图12.33所示，其中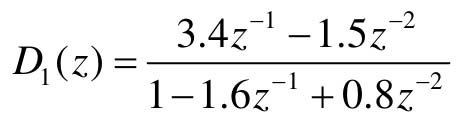H_367-01，G1是零阶保持器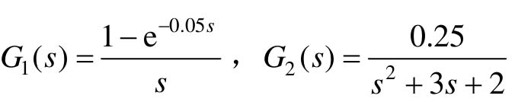，H_367-02，采样周期Ts=0.05s，试求系统开环和闭环Z传递函数以及S传递函数，当输入为单位阶跃函数时，试求其输出。

P_367-1

图12.33　采样离散控制系统

解：求取系统开环和闭环S传递函数的程序代码如下。

  1. dnum1=[3.4, -1.5]; dden1=[1, -1.6, 0.8];  Ts=0.05
  2. sysd1=tf(dnum1, dden1, Ts)     %建立z传递函数模型
  3. sysc1=d2c(sysd1, 'zoh')            % z传递函数模型转换成s传递函数模型
  4. num2=[0.25]; den2=[1, 3, 2]; sys2=tf(num2, den2)
  5. sysc2=sysc1*sys2;  sysbc=feedback(sysc2, 1)
  6. [num, den]=tfdata(sysbc, 'v')       %提取闭环传递函数的分子和分母
  7. p=rots(den)       %求闭环系统特征根

运行结果如下：

  1. Transfer function:       %数字控制器脉冲传
  2.    3.4 z - 1.5
  3. -----------------
  4. z^2 - 1.6 z + 0.8
  5. Sampling time: 0.05
  6. Transfer function:       %数字控制器转换为
  7.    55.97 s + 864.2
  8. ---------------------
  9. s^2 + 4.463 s + 90.97
  10. Transfer function:      %对象部分传递函数
  11.     0.25
  12. -------------
  13. s^2 + 3 s + 2
  14. Transfer function:      %系统开环传递函数
  15.                 13.99 s + 216
  16. ---------------------------------------------
  17. s^4 + 7.463 s^3 + 106.4 s^2 + 281.8 s + 181.9
  18. Transfer function:      %系统闭环传递函数
  19.                13.99 s + 216
  20. -------------------------------------------
  21. s^4 + 7.463 s^3 + 106.4 s^2 + 295.8 s + 398
  22. %求出特征方程的根，根都在S平面左半部，可见系统是稳定的。
  23. p=  -2.1667 + 9.1429i
  24.   -2.1667 - 9.1429i
  25.   -1.5647 + 1.4351i
  26.   -1.5647 - 1.4351i

求取系统开环和闭环Z传递函数程序代码如下：

  1. dnum1=[3.4, -1.5]; dden1=[1, -1.6, 0.8];  Ts=0.05
  2. sysd1=tf(dnum1, dden1, Ts)
  3. num2=[0.25]; den2=[1, 3, 2]; sys2=tf(num2, den2)
  4. sysd2=c2d(sys2, Ts, 'zoh')      %s传递函数模型转换成z传递函数模型
  5. sysd=sysd1*sysd2;  sysbd=feedback(sysd, 1)
  6. [dnum, dden]=tfdata(sysbd, 'v')     %提取闭环传递函数的分子和分母
  7. pd=roots(dden)         %求闭环系统特征根
  8. t=0:0.05:5
  9. y=dstep(dnum, dden, t)        %求闭环系统的单位阶跃响应
  10. stem(t, y)           %棒图显示响应曲线
  11. xlabel('t');  ylabel('y')
  12. grid

程序执行结果如下：

  1. Transfer function:       %数字控制器脉冲传递函数
  2.    3.4 z - 1.5
  3. -----------------
  4. z^2 - 1.6 z + 0.8
  5. Sampling time: 0.05
  6. Transfer function:      %对象部分传递函数
  7.     0.25
  8. -------------
  9. s^2 + 3 s + 2
  10. Transfer function:      %对象部分传递函数转换成z传递函数
  11. 0.0002973 z + 0.0002828
  12. -----------------------
  13. z^2 - 1.856 z + 0.8607
  14. Sampling time: 0.05
  15. Transfer function:      %系统开环z传递函数
  16.    0.001011 z^2 + 0.0005156 z - 0.0004242
  17. ---------------------------------------------
  18. z^4 - 3.456 z^3 + 4.63 z^2 - 2.862 z + 0.6886
  19. Sampling time: 0.05
  20. Transfer function:      %系统闭环z传递函数
  21.     0.001011 z^2 + 0.0005156 z - 0.0004242
  22. ----------------------------------------------
  23. z^4 - 3.456 z^3 + 4.631 z^2 - 2.861 z + 0.6881
  24. Sampling time: 0.05
  25. %求出特征方程的根，根都在z平面单位圆内，可见系统是稳定的。
  26. pd=   0.8030 + 0.3935i
  27.        0.8030 - 0.3935i
  28.        0.9250 + 0.0697i
  29.        0.9250 - 0.0697i

程序输出的图形如12.34所示。

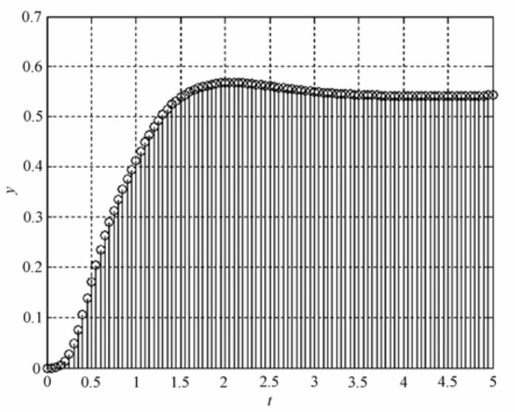
P_369-1

图12.34　单位反馈采样系统

【例12-11】　若某控制系统结构如图12.35所示，其中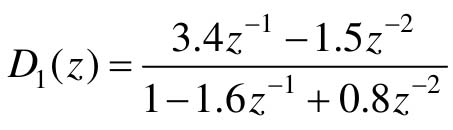H_369-01，G1是零阶保持器，H_369-02，采样周期Ts=0.05s，试求系统频率特性参数，并绘制Bode图、Nyquist图和Nichols图。

P_369-2

图12.35　采样离散控制系统

解：求系统开环脉冲传递函数频率响应的程序代码如下。

  1. dnum1=[3.4, -1.5];  dden1=[1, -1.6, 0.8];  Ts=0.05
  2. sysd1=tf(dnum1, dden1, Ts)
  3. num2=[0.25]; den2=[1, 3, 2];  sys2=tf(num2, den2)
  4. sysd2=c2d(sys2, Ts, 'zoh')
  5. sysd=sysd1*sysd2
  6. [dnumc, ddenc]=tfdata(sysd, 'v')        %提取开环传递函数的零极点
  7.  [Gm, Pm, Wcg, Wcp]=margin(sysd)      %求系统频率特性参数
  8. margin(sysd);  grid                %绘制Bode图
  9. w=0.01:0.01:100
  10. figure(2);  dnyquist(dnumc, ddenc, Ts, w); grid      %用nyquist函数绘制Nyquist图
  11. figure(3); nichols(sysd) ;  grid            %用nichols函数绘制Nyquist图
  12. 程序执行结果如下：
  13. Gm=   10.8194
  14. Pm=  133.7794
  15. Wcg=    6.4303
  16. Wcp=    0.5625

绘制的Bode图如图12.36所示。

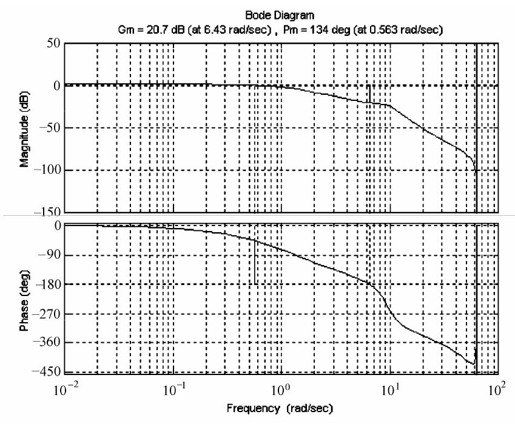
P_370-1

图12.36　Bode图及频率特性参数显示

绘制的Nyquist图如图12.37所示。

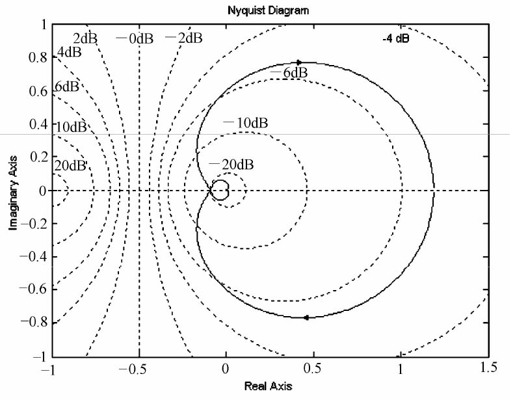
P_370-2

图12.37　Nyquist图

绘制的Nichols图如图12.38所示。

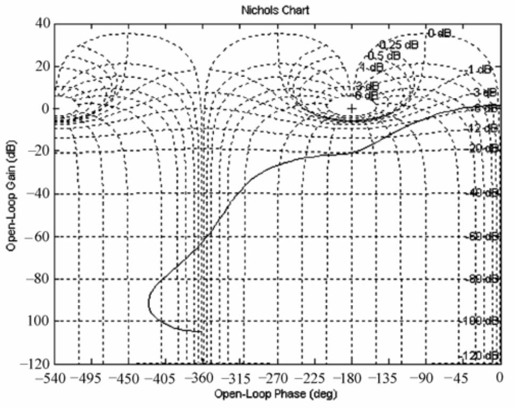
P_371-1

图12.38　Nichols图