11.6　综合实例及MATLAB/Simulink应用

下面通过一个综合实例，讲述MATLAB/Simulink在本章中的应用。

给定如图11.32所示的单位负反馈系统。

在系统中分别引入不同的非线性环节（饱和、死区与滞环），观察系统的阶跃响应，并且分析、比较不同的非线性环节对系统性能的影响。

解：使用MATLAB/Simunlink求解本题的基本步骤如下。

【步骤1】　利用MATLAB中的Simulink工具箱，对题设控制系统进行建模（如图11.32所示）。没有任何非线性环节的系统，其阶跃响应曲线如图11.33所示。

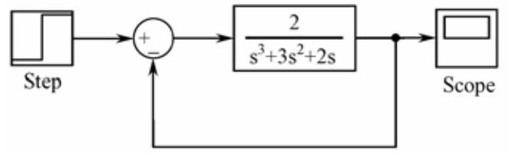
图11.32　给定单位负反馈系统

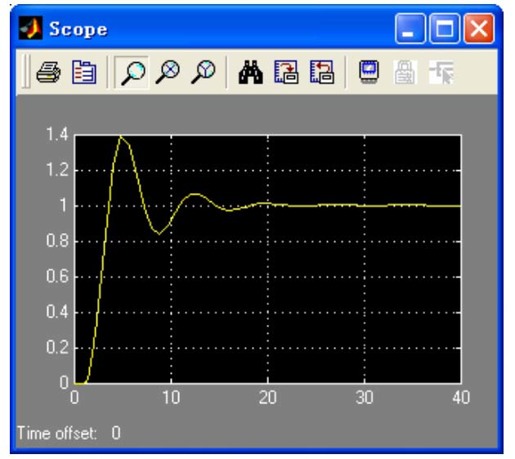
图11.33　未加入非线性环节的系统阶跃响应曲线

【步骤2】　在系统中加入饱和非线性环节，系统框图如图11.34所示。其中，饱和非线性环节的输出上限为0.1，输出下限为-0.1；阶跃信号幅值为1。

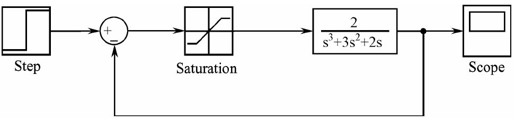
图11.34　加入饱和非线性环节后的系统框图

利用Simulink进行仿真，得到的阶跃响应曲线如图11.35所示。

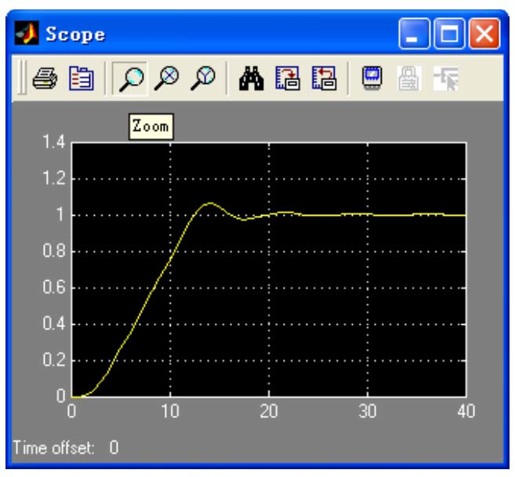
图11.35　加入饱和非线性环节后系统的阶跃响应曲线

为了比较当饱和非线性环节的输出上下限变化时系统阶跃响应的不同，可以利用Simulink中的To Workspace模块，将多次仿真的结果记录到工作空间的不同数组中，并且绘制在同一幅图像上。此时，系统框图如图11.36所示。

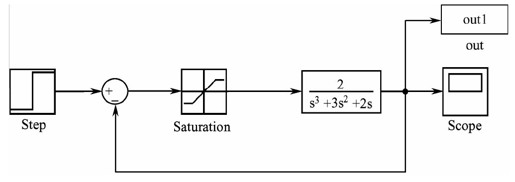
图11.36　利用To Workspace模块记录仿真的结果

设定饱和非线性环节输出上限为0.05，输出下限为-0.05，将仿真的结果记录到工作空间中的变量out1中；输出上限为0.1，输出下限为-0.1时，仿真结果存放在out2中；输出上限为0.2，输出下限为-0.2时，仿真结果存放在out3中；输出上限为0.5，输出下限为-0.5时，仿真结果存放在out4中。

将4种情况下系统的阶跃响应曲线绘制在同一幅图像中，代码如下：

plot(tout1,out1);        % 绘制第一条阶跃响应曲线
hold on;        % 设定在同一幅图像上绘制多条曲线
grid on;        % 显示网格线
gtext('0.05');       % 为曲线添加标注
plot(tout2,out2);        % 绘制第二条阶跃响应曲线
gtext('0.1');        % 为曲线添加标注
plot(tout3,out3);        % 绘制第三条阶跃响应曲线
gtext('0.2');        % 为曲线添加标注
plot(tout4,out4);        % 绘制第四条阶跃响应曲线
gtext('0.5');        % 为曲线添加标注

运行程序，结果如图11.37所示。

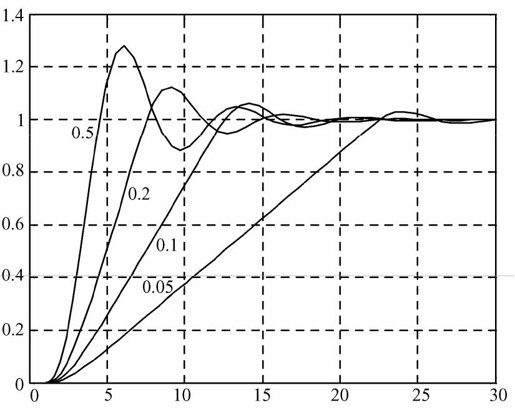
图11.37　加入不同的饱和非线性环节时系统的阶跃响应曲线

从图11.37中可以看出：当饱和非线性环节的输出范围较窄时，系统的阶跃响应速度较慢，上升时间长；同时，超调量较小，振荡不明显；随着输出范围的扩大，系统的响应速度加快，上升时间大大减少，同时伴有显著的振荡。

这是因为饱和环节会对信号起到限幅作用；不难想象，限制作用越强，系统的输出越不容易超调，响应也会越慢，这从图11.37也可看出这一趋势。

【步骤3】　在系统中引入死区非线性环节，系统框图如图11.38所示。其中，死区范围为[-0.1, 0.1]；阶跃信号幅值为1。

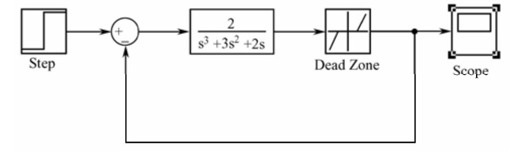
图11.38　加入死区非线性环节后的系统框图

利用Simulink进行仿真，得到的阶跃响应曲线如图11.39所示。

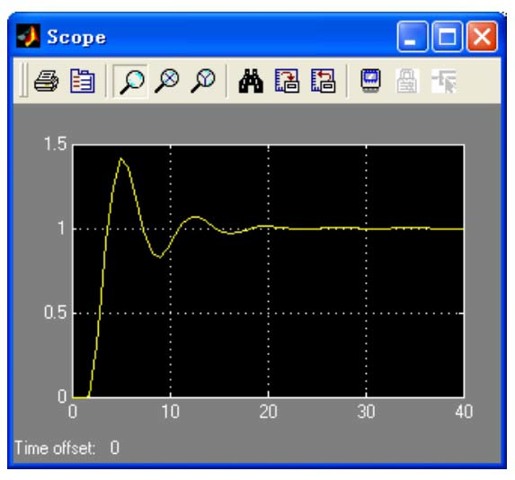
图11.39　加入死区非线性环节后系统的阶跃响应曲线

同样，为了对比死区范围不同时系统的阶跃响应，采用Simulink中的To Workspace模块，将仿真的结果保存在工作空间中的数组里。绘制阶跃响应曲线的代码同步骤2中完全类似。仿真结果如图11.40所示。

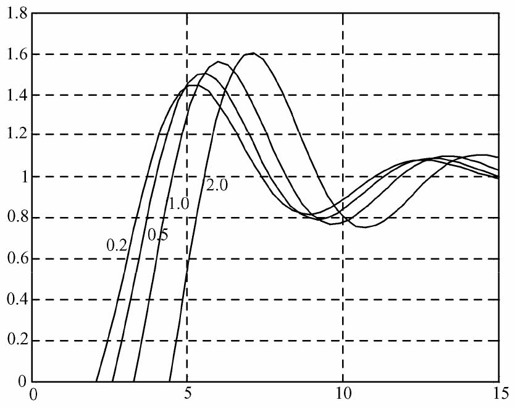
图11.40　加入不同的死区环节时系统的阶跃响应曲线

图中曲线上标注的0.2、0.5、1.0和2.0表示死区范围。不难看出，随着死区范围的增加，系统开始响应阶跃输入信号的时刻也逐渐推迟。这是因为死区环节会将死区内的输入“忽略”，使得系统的响应变慢。

【步骤4】　尝试在系统中同时加入死区单元和饱和单元，系统框图如图11.41所示。

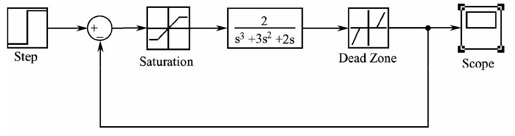
图11.41　同时引入饱和与死区非线性环节后的系统框图

利用Simulink进行仿真，得到的阶跃响应曲线如图11.42所示。

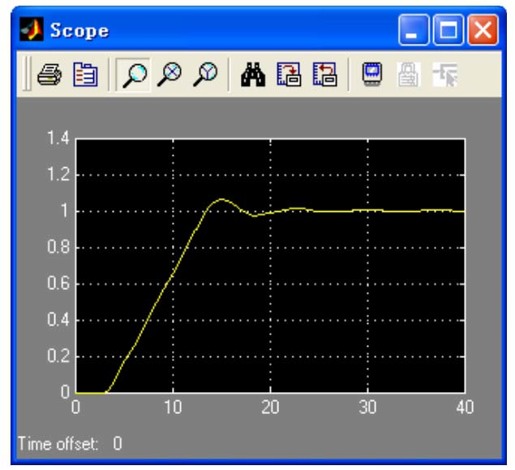
图11.42　同时引入饱和与死区非线性环节后系统的阶跃响应曲线

【步骤5】　在系统中引入滞环非线性环节，系统框图如图11.43所示。

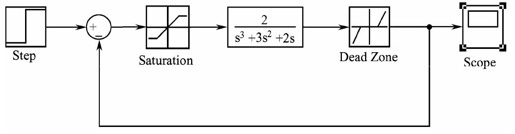
图11.43　加入滞环非线性环节后的系统框图

利用Simulink进行仿真，得到的阶跃响应曲线如图11.44所示。

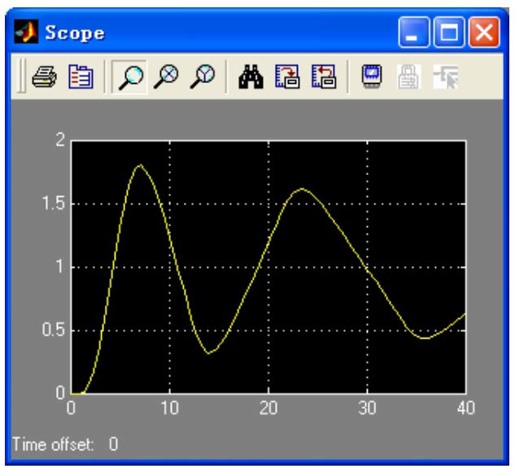
图11.44　加入滞环非线性环节后系统的阶跃响应曲线

改变滞环非线性环节中滞环的宽度，系统的阶跃响应曲线如图11.45所示。

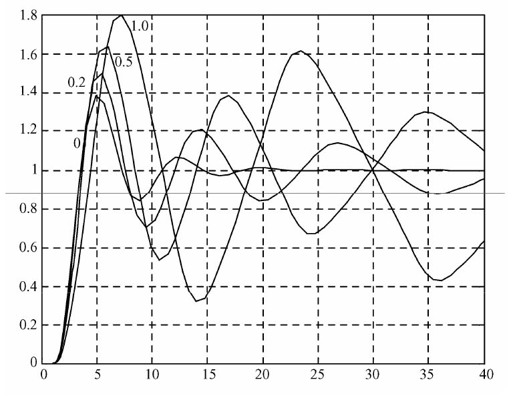
图11.45　加入不同滞环非线性环节时系统的阶跃响应曲线

图中曲线上标注的0、0.2、0.5和1.0表示滞环非线性环节中滞环的宽度。从图中不难看出，随着滞环宽度的增加，系统振荡加剧，变得越来越不稳定。所以说，滞环环节的引入会引起系统的振荡。

分析：对比以上各图，可以分析出非线性环节对控制系统稳定性能的影响：当系统中存在饱和非线性环节时，响应较慢，但是超调量减小；死区环节对0附近小范围内的输入信号无响应，而当输入超过这个“不灵敏区”后，输出与输入呈现出线性；同时，滞环环节会引起系统的振荡，使系统变得不稳定。

总结：非线性系统的相关理论和方法远远不及线性系统成熟，其特殊性导致没有普遍的研究非线性系统的方法。而利用Simulink，则可以很方便地完成对非线性系统的建模和仿真，为进一步的系统校正、综合提供基础。

习　题

【11.1】　给定非线性控制系统的结构如图11.A所示，其中，饱和环节的线性区为[-1,1]，斜率为1。试分析系统的稳定性，并绘制系统的阶跃响应曲线。

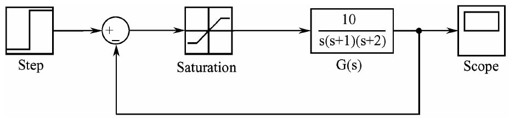
图11.A　习题

【11.2】　给定非线性控制系统的结构如图11.B所示。

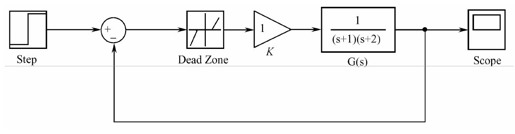
图11.B　习题

（1）在Simulink中建立上述系统的模型；

（2）设定开环增益为K=1，绘制系统的阶跃响应曲线；

（3）设定开环增益为K=10，绘制系统的阶跃响应曲线，并与第（2）问得到的曲线进行比较；

（4）继续修改K的取值，分析阶跃响应曲线的变化。