4.4　数学模型描述

为了对系统的性能进行分析首先要建立其数学模型，控制系统常用的模型有传递函数模型、零极点形式的数学模型和状态空间模型，下面分别进行讲述。

4.4.1　传递函数模型

传递函数是在拉氏变换的基础上，以系统本身的参数所描述的线性定常系统输入量和输出量的关系式，它表达了系统内在的固有特性，而与输入量或驱动函数无关。它可以是有量纲的，也可以是无量纲的，视系统的输入量、输出量而定，它包含着联系输入量与输出量所需要的量纲。它通常不能表明系统的物理特性和物理结构，许多物理性质不同的系统却有着相同的传递函数，正如一些不同的物理现象可以用相同的微分方程描述一样。

线性定常系统的传递函数定义为：在零初始条件下，输出量（响应函数）的拉普拉斯变换与输入量（驱动函数）的拉普拉斯变化之比。

考虑由下列微分方程描述的线性定常系统：

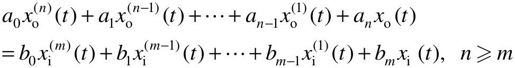
式中，xo为系统的输出量，xi为系统的输入量，在零初始条件下，输入量与输出量的拉普拉斯变换之比，就是这个系统的传递函数：

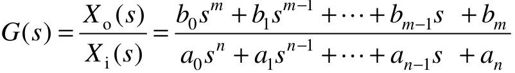
利用传递函数的概念，可以用以s为变量的代数方程表示系统的动态特性。如果传递函数分母中s的最高次数为n，则称该系统为n阶系统。

在自动控制中，传递函数是个非常重要的概念，它是分析线性定常系统的有力数学工具，它具有以下特点：

• 传递函数比微分方程简单，通过拉氏变换，实数域内复杂的微积分运算转化成代数运算；
• 当系统输入典型信号时，其输出与传递函数有一定对应关系，当输入是单位脉冲函数时，输入的象函数是1，其输出象函数与传递函数相同；
• 令传递函数中的s=jω，则系统可在频域内分析；
• 传递函数的零极点分布决定系统的动态特性。

对线性定常系统，式（4-5）中s的系数均为常数，且a0不等于0，这时系统在MATLAB中可以方便地由分子和分母多项式系数构成的两个向量唯一地确定出来，这两个向量分别用num和den表示。

num=[b0,b1,...,bm], den=[a0,a1,...,an]

则传递函数表示为：

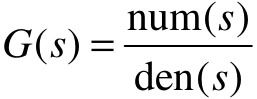
注意

它们都是按s的降幂进行排列的。

4.4.2　零极点形式的数学模型

零极点模型实际上是传递函数模型的另一种表现形式，其原理是分别对原系统传递函数的分子、分母进行分解因式处理，以获得系统零点和极点的表示形式。

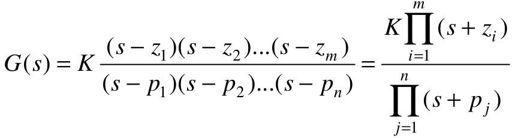
式中，K为系统增益；-zi（i=1,…,m）是分子多项式的根，称为系统的零点；-pj（j=1,…,n）是分母多项式的根，称为系统的极点。传递函数的分母多项式就是它的特征多项式，它等于零的方程就是传递函数的特征方程，特征方程的根也就是传递函数的极点。

传递函数的极点决定了所描述系统的自由运动模态，零点影响系统各模态在系统响应中所占的比重，这还会在后面章节详细论述。

控制系统常用到并联系统，这时就要对系统函数进行分解，使其表现为一些基本控制单元的和的形式，也就是用部分分式表示，如下式所示：

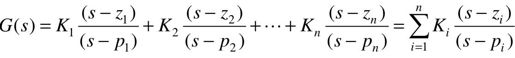
式中，Ki（i=1,…,n）为各个部分分式的增益；-zi（i=1,…,m）是分子多项式的根，称为系统的零点；-pj（j=1,…,n）是分母多项式的根，称为系统的极点。

4.4.3　状态空间模型

以传递函数为基础的经典控制理论的数学模型受当时手工计算的局限，着眼于系统的外部联系，重点为单输入单输出的线性定常系统。随着计算机的发展，以状态空间理论为基础的现代控制理论的数学模型则采用状态空间模型，以时域分析为主，着眼于系统的内部状态及其内部联系。

状态是系统动态信息的集合，在表征系统信息的所有变量中，能够全部描述系统运行的最小数目的一组独立变量称为系统的状态变量，其选取不是唯一的。所谓状态方程是由系统状态变量构成的一阶微分方程组。

具有n个状态、r个输入和m个输出的线性时不变系统，用矩阵符号表示的状态空间模型如下：

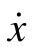=Ax+Bu（状态方程）

y=Cx+Du（输出方程）

式中，状态向量x是n维的，输入向量u是r维的，输出向量y是m维的，状态矩阵A是n×n维的，输入矩阵B是n×r维的，输出矩阵C是m×n维的，前馈矩阵D是m×r维的，对于一个时不变系统，A、B、C、D都是常数矩阵。