4.2　动态过程微分方程描述

4.2　动态过程微分方程描述

微分方程是控制系统模型的基础，一般来讲，利用机械学、电学、力学等物理规律便可以得到控制系统的动态方程，这些方程对于线性定常连续系统而言是一种常系数的线性微分方程。

控制系统动态微分方程的建立基于以下两个条件：

（1）在给定量产生变化或扰动出现之前，被控制量的各阶导数都为零，即系统是处于平衡状态的，因此，在任一瞬间，由各种不同环节组成的自动控制系统用几个独立变量就可以完全确定系统的状态。

（2）建立的动态微分方程式是以微小增量为基础的增量方程，而不是其绝对值的方程，因此，当出现扰动或给定量产生变化时，被控量和各独立变量在其平衡点附近将产生微小的增量，微分方程式描述的是微小偏差下系统运动状态的增量方程，不是运动状态变量的绝对值方程，也不是大偏差范围内的增量方程。

动态微分方程描述的是被控制量与给定量或扰动量之间的函数关系，给定量和扰动量可以看成系统的输入量，被控制量看成输出量。建立微分方程时，一般从系统的环节着手，先确定各环节的输入量和输出量，以确定其工作状态，并建立各环节的微分方程，而后消去中间变量，最后得到系统的动态微分方程。

【例4-1】　建立如图4.1所示的LRC电路的微分方程式。

083-1

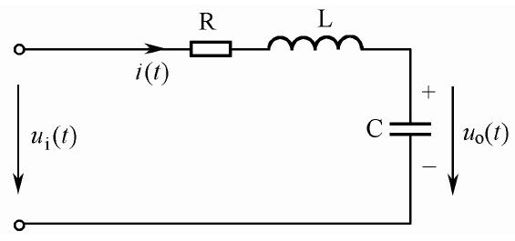
图4.1　RLC电路示意图

解：本题的基本解题步骤如下。

【步骤1】　确定电路的输入和输出量。

由图可知，当电压ui(t)发生变化时，将引起电路中电流i(t)的变化，因此uo(t)也将随着变化。在这里，取电路的输入量为ui(t)，以下式表示：

xcause=ui(t)

取输入量为uo(t)，以下式表示：

xcause=uo(t)

这两个量都是时间的函数，而回路中的电路i(t)则为联系输入和输出的中间变量。

【步骤2】　列出原始微分方程式。

根据基尔霍夫电压定律、电流定律得到系统的原始微分方程为：

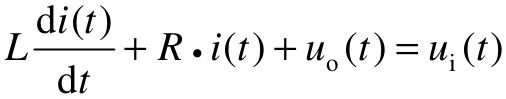
084gs-1

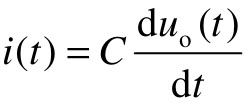
084gs-2

【步骤3】　消去中间变量。

联立以上方程式，消去中间变量i(t)，可得到电路微分方程式：

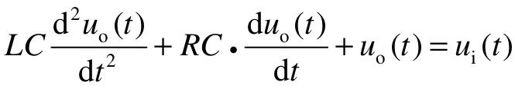
084gs-3

或

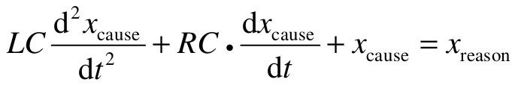
084gs-4

对于比较复杂的系统，建立系统微分方程一般可采用以下步骤：

（1）将系统划分为多个环节，确定各环节的输入及输出信号，每个环节可考虑写一个方程；

（2）根据物理定律或通过实验等方法得出物理规律，列出各环节的原始方程式，并考虑适当简化、线性化；

（3）将各环节方程式联立，消去中间变量，最后得出只含有输入变量、输出变量以及参量的系统方程式。

单输入单输出系统微分方程表示的输入模型一般具备如下形式：

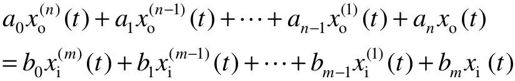
084gs-5

如果已知输入量及变量的初始条件，对微分方程进行求解，就可以得到系统输出量的表达式，并由此对系统进行性能分析。MATLAB提供了ode23、ode45等微分方程的数值解法函数，不仅适用于线性定常系统，也适用于非线性和时变系统。

【例4-2】　电路如图4.2所示，R=1.6Ω，L=2.1H，C=0.30F，初始状态是电感电流为零，电容电压为0.2 V，t=0时接入1.5 V的电压，求0<t<10s时i(t)，uo(t)的值，并画出电流与电容电压的关系曲线。

084-6

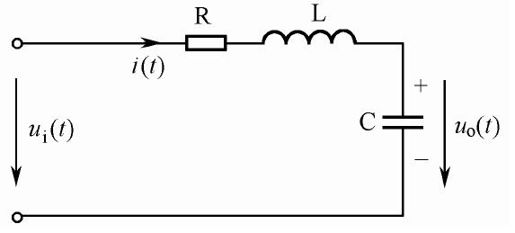
图4.2　RLC电路示意图

解：程序主函数的MATLAB代码如下。

clear all                                    %清除工作空间的变量
t0=0; tfinal=10;                            %响应时间
x0=[0.2;0];                                  %初始化，电感电流为0，电容电压为0.2V
[t, x]=ode45('rlcsys', t0, tfinal, x0);      %rlcsys是系统微分方程的描述函数
figure(1); subplot(211); plot(t, x(:, 1));  grid  %绘制状态响应图并添加栅格
title('电容电压/V'); xlabel('时间/s')        %添加图标题和标示横坐标轴
subplot(212); plot(t, x(:, 2)); grid      %绘制状态响应图并添加栅格
title('电感电流/A'); xlabel('时间/s')       %添加图标题并标示横坐标轴
figure(2); vc=x(:, 1); i=x(:, 2);
plot(vc, i); grid
title('电感电流与电容电压的关系曲线')        %添加图标题
xlabel('电容电压/v'); ylabel('电感电流/A') %标示横、纵坐标轴

系统微分方程描述函数的MATLAB如下：

function xdot=rlcsys(t, x)          %微分方程函数，状态导数
Vs=1.5; R=1.6; L=2.1; C=0.30;       %电压、电阻、电感、电容值
xdot=[x(2)/C;1/L*(Vs-x(1)-R*x(2))]; %导数关系式
%  function xdot=filename(t, x)     %格式
%  xdot=[表达式1；表达式2；表达式3；…；表达式n-1]
%  表达式1对应x1'=x2;       表达式2对应x2'=x3
%  表达式3对应x3'=x4    …    表达式n-1对应xn-1'=xn
%  本例中, x(1)=Vo, x(2)=iL, x(1)'=x(2)/C, x(2)'=(Vs-x(1)-R*x(2))/L

程序运行结果如图4.3和图4.4所示，图4.3为i(t)和uo(t)的时间关系曲线，图4.4为电流与电容电压的关系曲线。

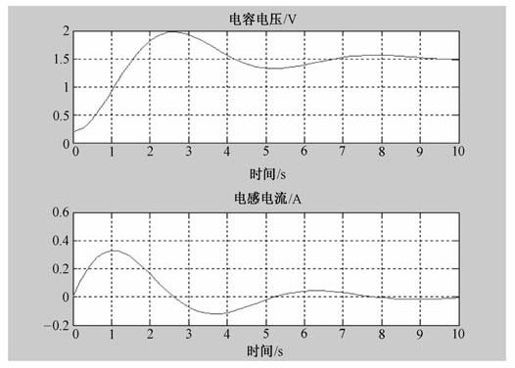
085-01

图4.3　i(t)和uo(t)的时间关系曲线

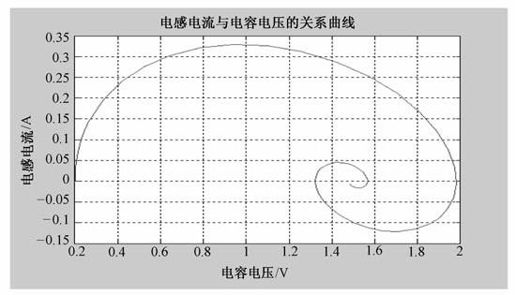
085-02

图4.4　电流与电容电压的关系曲线

4.2 动态过程微分方程描述