11.4　描述函数法

描述函数法是达尼尔（P. J. Daniel）于1940年提出的，它是线性系统频率法在非线性系统中的推广，是非线性系统稳定性的近似判别法，它要求系统具有良好的低通特性且非线性较弱，描述函数法的优点是能用于高阶系统。

11.4.1　描述函数基本概念

在频率法中，对于线性时不变系统，当输入为正弦函数时输出也是同频率的正弦函数，输出和输入只有幅值和相位的差别。对于非线性系统，当输入为正弦函数时，输出是同频率的非正弦函数，也就是说输出中含有高次谐波，可见线性系统的频率法不适用于非线性系统。描述函数的作用相当于对线性系统中的频率法进行改进并使之适用于非线性系统。

描述函数的基本思想：当系统满足一定的假设条件时，系统中非线性环节在正弦信号作用下的输出可用一次谐波分量来近似，由此导出非线性环节的近似等效频率特性，即描述函数。这样，非线性系统就近似等效为一个线性系统，并可用线性系统理论中的频率法对系统进行频域分析。

11.4.2　描述函数定义

对于如图11.23所示的非线性系统，其中N是非线性环节，它的输入/输出关系为y(t)=f(x(t))，线性部分的传递函数为G(s)。

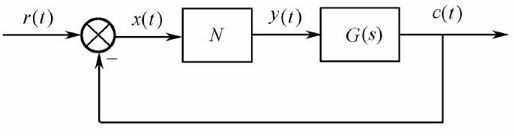
图11.23　非线性系统框图

当非线性环节的输入为如下正弦函数时：

式中，X是正弦函数的幅值。

将非线性环节的输出y(t)分解为傅里叶级数，有

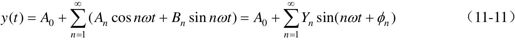
式中，A0是直流分量；An,Bn是傅里叶系数；Yn,φn分别是第n次谐波分量的幅值和相角，且

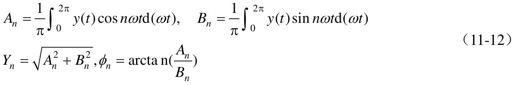
如果非线性特性是奇对称的，那么直流分量A0=0，式（11-11）可简化为

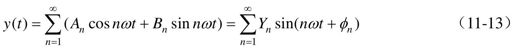
式（11-13）表明，非线性环节的输出y(t)中含有高次谐波。如果系统线性部分具有良好的低通滤波特性，那么系统信号中高次谐波就被大大衰减，即当n>1时Yn会很小，因此可以用基波来近似，如式（11-14）所示。

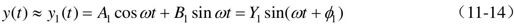
可以看出，非线性环节可近似为与线性环节类似的频率响应形式，这就是非线性特性在频域的线性化。

在正弦信号输入下可用非线性环节输出中的基波分量和输入正弦函数的复数比来描述这个非线性环节，如式（11-15）所示。

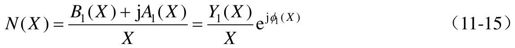
式中，幅值X是一个待定常数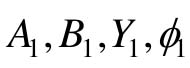；只与X有关，记为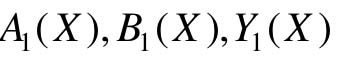和φ1(X)；N(X)称为非线性环节y(t)=f(x(t))的描述函数。

显然，描述函数是幅值X的函数，描述函数可以理解为非线性环节在忽略高次谐波情况下的非线性增益——这个增益与输入正弦函数的幅值有关。如果非线性特性是单值奇对称的，那么。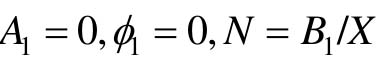

这相当于用一个等效环节代替原来的非线性环节，而等效环节的幅相特性函数N(X)是输入函数x(t)=X sin ωt幅值X的函数，这样，图11.23就可等效为图11.24。

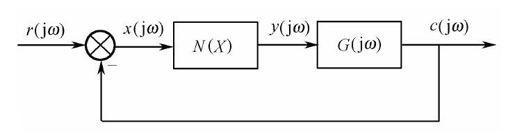
图11.24　非线性系统等效框图

11.4.3　描述函数的计算

当非线性环节的频率特性用描述函数表示后，线性系统中普遍应用的频率法就可以推广到非线性系统了，问题的关键是非线性环节描述函数如何计算。

描述函数求解的基本过程是：先根据已知的输入x(t)=X sin ωt和非线性特性y(t)=f(x(t))求出输出y(t)，然后通过积分求出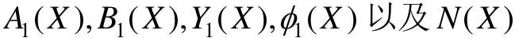。其工作量和技巧主要在积分。

下面举例说明描述函数的计算过程。

对于如图11.1所示的死区非线性，当输入为正弦函数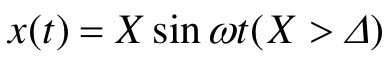时，输出y(t)为

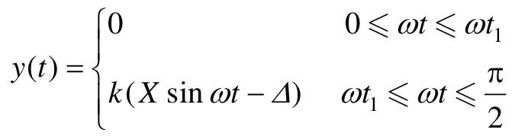
式中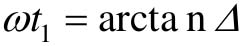，，由于图中的死区非线性是单值奇对称的，因此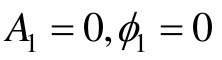，且

代入即可得理想死区非线性的描述函数，即

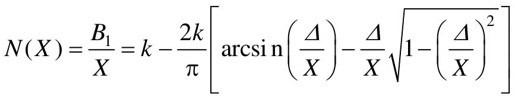
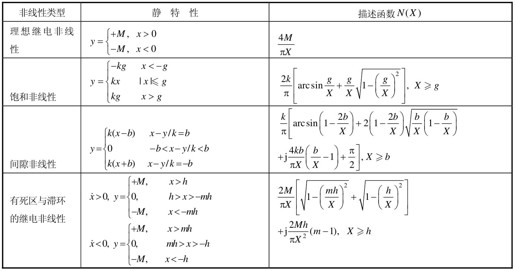
表11.1列出了一些典型非线性描述函数，以供查用。

表11.1　典型非线性描述函数

11.4.4　非线性系统的稳定性分析

对于如图11.25所示的非线性控制系统，N表示非线性部分，G(s)表示线性部分，

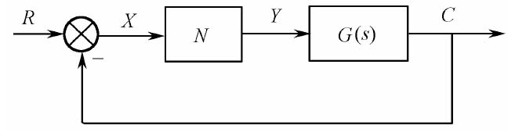
图11.25　非线性系统框图

则闭环系统频率特性为

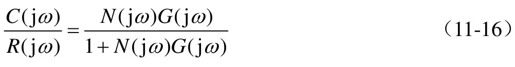
特征方程为

如果非线性部分用放大系数k来表示，即N(X)=k，则特征方程与线性系统的特征方程相似。式（11-17）可表示为

或

式（11-18）用线性部分的频率特性的逆与负描述函数特性比较，式（11-19）用负倒描述函数与频率特性比较，它们常用于非线性系统的稳定性分析。

非线性系统稳定条件为：线性部分频率特性G(jω)的逆应包围非线性部分描述函数负值-N(jω)的点；或者，线性部分的（-1, 0）稳定点的判别被描述函数的负倒数代替。将描述函数的负倒数的轨迹作为判别点轨迹，则系统稳定判据如下：

（1）在复平面上，如果曲线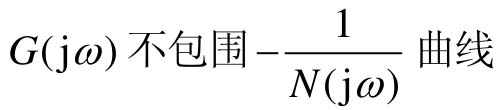，那么闭环系统稳定，两者的距离越远，系统越稳定；

（2）在复平面上，如果，那么闭环系统不稳定；

（3）在复平面上，如果曲线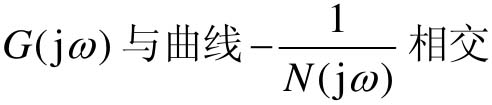，那么闭环系统临界稳定，闭环系统出现自激振荡（极限环）。

为了方便起见，通常将曲线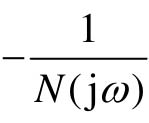称为“负倒描述函数曲线”。