1.4　控制系统仿真基本概念

系统仿真作为一种特殊的试验技术，在20世纪30～90年代的半个多世纪中经历了飞速发展，到今天已经发展成为一种真正的、系统的实验科学。伴随着第一台电子管电子计算机的诞生和以相似理论为基础的模拟技术的应用，仿真作为一种研究、发展新产品、新技术的科学手段，在航空、航天、造船、兵器等与国防科研相关的行业中首先发展起来，并显示了巨大的社会效益和经济效益。

以武器的作战使用训练为例，1930年前后，美国陆、海军航空队就使用了林克式仪表飞行模拟训练器。当时其经济效益相当于每年节约1.3亿美元，而且少牺牲524名飞行员，此后，固定基座及三自由度飞行模拟座舱陆续大量投入使用。1950—1953年，美国首先利用计算机来模拟战争，防空兵力或地空作战被认为是具有最大训练潜力的应用范畴。20世纪60年代，目标探测、捕获、跟踪和电子对抗已经进入了仿真系统。70年代利用放电影方式，在大球幕内实现了多目标、飞机-导弹作战演习。随着80年代数字计算机的高速发展，训练仿真开始蓬勃发展，甚至呈现了两个新概念，即武器系统研制与训练装置的开发同步进行以及训练装置作为武器系统可嵌入的组成部分而进入整个计算机软件系统。至于武器的控制与制导（C&G）系统研制、试验与定型中仿真技术的应用则更为普遍。在80年代对于导弹的研制中，由于采用仿真使飞行试验数量减小了30%～40%，节约研制经费10%～40%，缩短周期30%～60%，这足以说明系统仿真在工程应用中的重大意义。

仿真的基本思想是利用物理的或数学的模型来类比模仿现实过程，以寻求对真实过程的认识，它所遵循的基本原则是相似性原理。

1.4.1　计算机仿真基本概念

计算机仿真是基于所建立的系统仿真模型，利用计算机对系统进行分析与研究的技术与方法。

1.4.1.1　模型

模型是对现实系统有关结构信息和行为的某种形式的描述，是对系统特征与变化规律的一种定量抽象，是人们认识事物的一种手段或工具。

模型可以分为以下三类：

（1）物理模型，指不以人的意志为转移的客观存在的实体。例如，飞行器研制中的飞行模型、船舶制造中的船舶模型等。

（2）数学模型，指从一定的功能或结构上进行相似，用数学的方法来再现原型的功能或结构特征。

（3）仿真模型，指根据系统的数学模型，用仿真语言转化为计算机可以实现的模型。

1.4.1.2　仿真分类

可以从模型角度和计算机类型角度对不同的仿真系统进行分类。

1. 按模型分类

（1）物理仿真：采用物理模型，有实物介入，具有效果逼真、精度高等优点，但造价高或耗时长，大多在一些特殊场合下采用（如导弹、卫星一类飞行器的动态仿真，发电站综合调度仿真与培训系统等），具有实时、在线的特点。

（2）数学仿真：采用数学模型。它在计算机上进行，具有非实时、离线的特点，经济、快速、实用。

1. 按计算机类型分类

（1）模拟仿真：采用数学模型，在模拟计算机上进行的仿真实验。这是一种早期的仿真手段，现在基本被淘汰。它的特点是描述连续物理系统的动态过程比较自然、逼真，具有仿真速度快、失真小、结果可靠的优点，但受元器件性能影响，仿真精度较低，对计算机控制系统的仿真较困难，自动化程度低。模拟计算机的核心是运算部分，它由我们熟知的“模拟运算放大器”为主要构成部件。

（2）数字仿真：采用数学模型，在数字计算机上借助数值计算方法所进行的仿真实验。它是在20世纪60年代随着计算机的发展而发展起来的，其特点是计算与仿真的精度较高。理论上计算机的字长可以根据精度要求来“随意”设计，因此其仿真精度可以是无限的，但是由于受到误差积累、仿真时间等因素影响，其精度也不易定得太高。它对计算机控制系统的仿真比较方便，仿真实验的自动化程度较高，可方便地实现显示、打印等功能，但计算速度比较低，在一定程度上影响到仿真结果的可信度。随着计算机技术的发展，速度问题会在不同程度上有所改进与提高。数字仿真没有专用的仿真软件支持，需要设计人员用高级程序语言编写求解系统模型及结果输出程序。

（3）混合仿真：结合了模拟仿真与数字仿真的技术与特点。

（4）现代计算机仿真：采用先进的微型计算机，基于专用的仿真软件、仿真语言来实现，其数值计算功能强大，易学易用。它是在20世纪80年代发展起来的，是当前主流的仿真技术与方法。

1.4.1.3　仿真应用

仿真技术有着广泛的应用，而且应用的深度和广度也越来越大，目前主要应用在以下方面：

（1）航空与航天工业，包括飞行器设计中的三级仿真体系（即纯数学仿真）、半实物仿真、实物仿真或模拟飞行实验，飞行员及宇航员训练用飞行仿真模拟器等。

（2）电力工业，包括电力系统动态模型实验，电力系统负荷分配、瞬态稳定性以及最优潮流控制，电站操作人员培训模拟系统等。

（3）原子能工业，包括模拟核反应堆，核电站仿真器，用来训练操作人员以及研究异常故障的排除处理等。

（4）石油、化工及冶金工业。

（5）非工程领域，如医学、社会学、宏观经济和商业策略的研究等。

1.4.1.4　仿真技术应用意义

仿真技术的应用具有重要的意义，主要体现在以下方面：

（1）经济。大型、复杂系统直接实验是十分昂贵的，如空间飞行器一次飞行实验的成本在1亿美元左右，而采用仿真实验仅需其成本的1/10～1/5，而且设备可以重复使用。

（2）安全。某些系统，如载人飞行器、核电装置等，直接实验往往会有很大的危险，甚至是不允许的，而采用仿真实验可以有效降低危险程度，对系统的研究起到保障作用。

（3）快捷。提高设计效率，如电路设计、服装设计等。

（4）具有优化设计和预测的特殊功能。对一些真实系统进行结构和参数的优化设计是非常困难的，这时仿真可以发挥它特殊的优化设计功能。再如在非工程系统，如社会、管理、经济等系统，由于其规模及复杂程度巨大，直接实验几乎是不可能的，这时通过仿真技术与方法的应用可以获得对系统的某种超前认识。

1.4.2　控制系统仿真

控制系统仿真是系统仿真的一个重要分支，它是一门涉及自动控制理论、计算数学、计算机技术、系统辨识、控制工程以及系统科学的综合性新型学科。它为控制系统的分析、计算、研究、综合设计以及控制系统的计算机辅助教学等提供了快速、经济、科学及有效的手段。

控制系统仿真就是以控制系统模型为基础，采用数学模型替代实际控制系统，以计算机为工具，对控制系统进行实验、分析、评估及预测研究的一种技术与方法。

控制系统仿真通过控制系统的数学模型和计算方法，编写程序运算语句，使之能自动求解各环节变量的动态变化情况，从而得到关于系统输出和所需要的中间各变量的有关数据、曲线等，以实现对控制系统性能指标的分析与设计。

1.4.3　控制系统计算机仿真基本过程

控制系统仿真包括以下几个基本步骤：问题描述、模型建立、仿真实验、结果分析，其流程如图1.5所示。

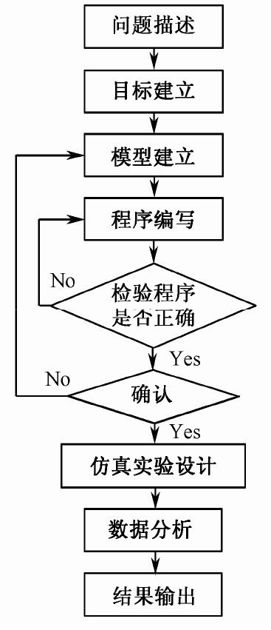
图1.5　计算机仿真流程图

1. 建立数学模型

控制系统模型，是指描述控制系统输入、输出变量以及内部各变量之间关系的数学表达式。控制系统模型可分为静态模型和动态模型，静态模型描述的是控制系统变量之间的静态关系，动态模型描述的是控制系统变量之间的动态关系。最常用、基本的数学模型是微分方程与差分方程。控制系统数学模型的建立将在第4章中进行详细的论述。

1. 建立仿真模型

由于计算机数值计算方法的限制，有些数学模型是不能直接用于数值计算的，如微分方程，因此原始的数学模型必须转换为能够进行系统仿真的仿真模型。例如，在进行连续系统仿真时，就需要将微分方程这样的数学模型通过拉普拉斯变换转换成传递函数结构的仿真模型。

1. 编写仿真程序

控制系统的仿真涉及很多相关联的量，这些量之间的联系要通过编制程序来实现，常用的数值仿真编程语言有C、FORTRAN等，近年来发展迅速的综合计算仿真软件，如MATLAB/Simulink也可以用来编写仿真程序，而且编写起来非常迅速、界面友好，已得到了广泛应用，本书将结合MATLAB/Simulink来对控制系统仿真进行阐述。

1. 进行仿真实验并分析实验结果

在完成以上工作后，就可以进行仿真实验了，通过对仿真结果的分析来对仿真模型与仿真程序进行检验和修改，如此反复，直至达到满意的实验效果为止。

1.4.4　计算机仿真技术发展趋势

随着计算机技术的发展与进步，与之紧密结合的计算机仿真技术也得到了飞速发展，其发展趋势主要体现在以下方面。

（1）硬件方面：基于多CPU并行处理技术的全数字仿真将有效提高仿真系统的速度，大大增强数字仿真的实时性。

（2）应用软件方面：直接面向用户的数字仿真软件不断推陈出新，各种专家系统与智能化技术将更深入地应用于仿真软件开发之中，使得在人机界面、结果输出、综合评判等方面达到更理想的境界。

（3）分布式数字仿真：充分利用网络技术进行分布式仿真，投资少，效果好。

（4）虚拟现实技术：综合了计算机图形技术、多媒体技术、传感器技术、显示技术以及仿真技术等多学科，使人仿佛置身于真实环境之中，这就是“仿真”追求的最终目标。