4.5　MATLAB/Simulink在模型中的应用

由于传递函数表示为多项式之比的形式，因此下面先讲述MATLAB中多项式处理相关的函数。

4.5.1　多项式处理相关的函数

MATLAB中多项式用行向量表示，行向量元素依次为降幂排列的多项式的系数。

  1. 多项式乘法函数conv()

MATLAB中提供的卷积分函数conv()可以用来进行多项式乘法处理，其常见的函数调用格式为：

  1. C=conv(A,B)

其中，A和B分别表示一个多项式的系数（通常是降幂排列），C为A和B多项式的乘积多项式。

注意

conv()函数的调用允许多级嵌套。

  1. 多项式求根函数roots()

传递函数G(s)输入之后，分别对分子和分母多项式进行因式分解，则可求出系统的零极点。

MATLAB中提供了多项式求根函数roots()，其常见的函数调用格式为：

  1. r= roots(p)

其中，p为多项式，r为所求的根。

  1. 由根创建多项式函数poly()

如果已知多项式的因式分解式或特征根r，可用MATLAB函数poly()直接得出特征多项式系数矢量p，其常见的调用格式为：

  1. p=poly(r)

可见，函数roots( )与函数poly( )互为逆运算。

  1. 求多项式在给定点的值函数polyval()

如果已知多项式p，要求其变量取a时的值v，可用MALAB中的函数polyval( )来求取，其常见的调用格式为：

  1. v=polyval(p,a)

4.5.2　建立传递函数相关的函数

假设系统是单输入单输出（SISO）系统，其输入、输出分别用u(t)、y(t)来表示，则得到线性系统的传递函数模型：

090-1

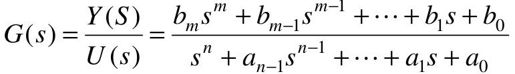
在MATLAB语言中，可以利用传递函数分子、分母多项式的系数向量进行描述，分子num、分母den多项式的系数向量分别为：

090-2

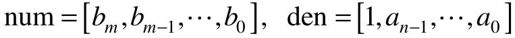
这里分子、分母多项式系数按s的降幂排列。

  1. 建立传递函数模型的函数tf()

MATLAB提供了建立传递函数模型的函数tf()，其常见的调用格式如下：

（1）sys=tf(num, den)。

（2）sys=tf(num, den, 'InputDelay', tao)。

其中，num是分子多项式系数行向量，den是分母多项式系数行向量，sys是建立的传递函数。

调用格式（1）建立的是常规系统G(s)的传递函数。调用格式（2）建立的是带时间延迟的系统Gd(s)=G(s)e-τs的传递函数，其中InputDelay为关键词，也可写成OuputDelay，对于线性SISO系统，二者是等价的。tao为系统延迟时间τ的数值。

  1. 提取模型中分子分母多项式系数的函数tfdata()

对于已经建立的传递函数模型，MATLAB提供了函数tfdata()，可以从传递函数模型中提取模型中的分子分母多项式系数，其常见的调用格式如下：

  1. [num, den] =tfdata(sys,'v')

其中，v为关键词，其功能是返回列向量形式的分子分母多项式系数。

4.5.3　建立零极点形式的数学模型相关函数

假设系统是单输入单输出系统（简称SISO），其零极点模型表示为：

091-1

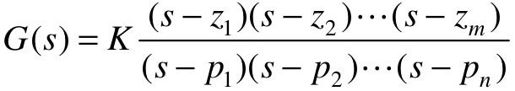
其中，Zi（i=1,2,…,m）和Pi（i=1,2,…,n）分别为系统的零点和极点，K为系统的增益。[z]、[p]、[k]分别为系统的零极点和增益向量。

  1. 建立零极点形式数学模型的函数zpk()

MATLAB提供了建立零极点形式的数学模型zpk()，其常见的调用格式如下：

（1）sys=zpk([z],[p],[k])。

（2）sys=zpk(z,p,k,'InputDelay',tao)。

其中，[z]、[p]、[k]分别为系统的零极点和增益向量，sys是建立的零极点形式的数学模型。

格式（1）建立的是常规系统G(s)的零极点形式的数学模型，格式（2）建立的是带时间延迟的系统Gd(s)=G(s)e-τs的零极点形式的数学模型，其中InputDelay为关键词，也可写成OuputDelay，对于线性SISO系统，二者是等价的。tao为系统延迟时间τ的数值。

  1. 提取模型中零极点和增益向量的函数zpkdata()

对于已经建立的零极点形式的数学模型，MATLAB提供了函数zpkdata()，可以从模型中提取出模型中的零极点和增益向量，其常见的调用格式如下：

  1. [z, p, k]=zpkdata(sys, 'v')

其中，v为关键词，其功能是返回列向量形式的零极点和增益向量。

  1. 传递函数模型部分分式展开的函数residue()

MATLAB提供了函数residue()，它的功能是对两个多项式的比进行部分展开，以及把传递函数分解为微分单元的形式，其常见的调用格式如下：

  1. [r, p, k]=residue(b, a)

其中，向量b和a是按s的降幂排列的多项式系数。部分分式展开后，余数返回到向量r，极点返回到列向量p，常数项返回到k。

[b, a]=residue(r, p, k)可以将部分分式转化为多项式比p(s)/q(s)。

4.5.4　建立状态空间模型相关的函数

状态方程是研究系统最有效的系统数学描述，在引进相应的状态变量后，可将一组一阶微分方程表示成状态方程的形式。在MATLAB中，系统状态空间用（A, B, C, D）矩阵组表示。

  1. 建立状态空间模型的函数ss()

MATLAB提供了建立状态空间模型的函数ss()，其常见的调用格式如下：

  1. sys=ss(A,B,C,D)

其中，(A, B, C, D)为系统状态空间的矩阵组表示，sys是建立的状态空间模型。

  1. 提取模型中状态空间矩阵的函数ssdata()

对于已经建立的状态空间模型，MATLAB提供了函数ssdata()，可以从模型中提取出模型的状态空间矩阵，其常见的调用格式如下：

  1. [A,B,C,D]=ssdata(sys)

其中，sys是建立的状态空间模型，[A, B, C, D]为系统状态空间的矩阵。

4.5.5　Simulink中的控制系统模型表示

在Simulink基本模块中选择“Continuous”后，单击便看到其中包括的连续模块，它包括的子模块及功能如表4.3所示。

表4.3　连续模块的名称及功能

092-5

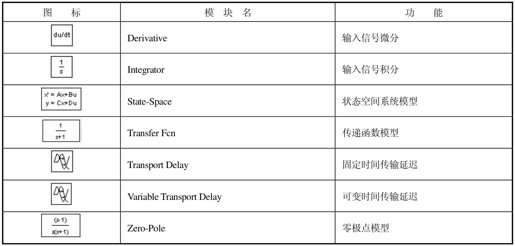
使用这些模块进行仿真时，将图标拖到Simulink的模型窗口中，双击图标就打开了其属性设置对话框，设置具体的模型系数即可。

例如，要建立传递函数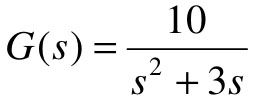092-6的模型，将“Transfer Fcn”图标拖到模型窗口，双击传递函数打开其属性设置对话框，并将其中的Numerator设置为“[10]”，Denominator设置为“[1 3 0]”，便建立了传递函数的模型，如图4.6所示。

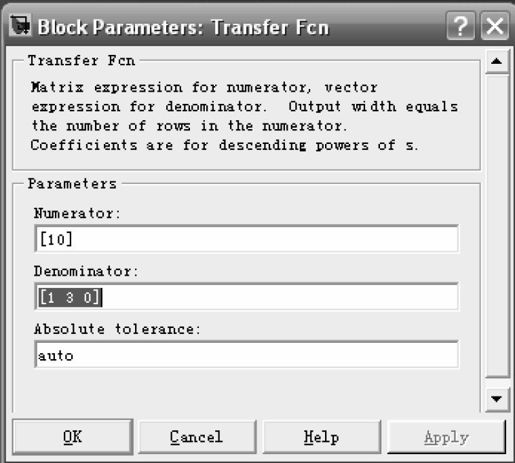
093-01

图4.6　模块参数设置对话框

4.5.6　Simulink中模型与状态空间模型的转化

Simulink提供了以状态空间形式线性化模型的函数命令：linmod和dlinmod，这两个命令需要提供模型线性化时的操作点，它们返回的是围绕操作点处系统线性化的状态空间模型。linmod命令执行的是连续系统模型的线性化，linmod2命令也是获取线性模型，采用高级方法，而dlinmod命令执行的是离散系统模型的线性化。

linmod命令返回的是由Simulink模型建立的常微分方程系统的线性模型，命令的语法结构为：

  1. [A, B, C, D] = linmod ('sys', x, u)

这里，sys是需要进行线性化的Simulink模型系统的名称，linmod命令返回的就是sys系统在操作点处的线性模型。x是操作点处的状态向量；u是操作点处的输入向量，如果删除x和u，缺省值为0。

需要注意的是，linmod函数如果要线性化包含微分（Derivative）或传输滞后（Transport Delay）模块的模型时会比较麻烦，在线性化之前，需要用一些专用模块替换这两个模块，以避免产生问题。

这些模块在Simulink Extras库下的Linearization子库中：

（1）对于Derivative模块，用Linearization子库中的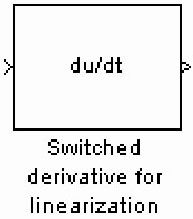093-1Switched derivative for linearization模块替换；

（2）对于Transport Delay模块，用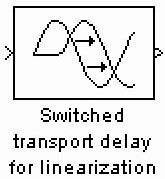093-2Switched transport delay for linearization模块替换（这些模块要求系统中安装了Control System Toolbox）。

当模型中有Derivative模块时，也可以试试把导数模块与其它模块合并起来。例如，如果一个Derivative模块与一个Transfer Fcn模块串联，最好用单个一个Transfer Fcn模块实现。

4.5.7　应用实例

下面通过几个典型的应用实例讲述MATLAB/Simulink在模型中的应用。

【例4-4】　求传递函数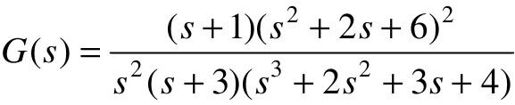094-1的分子和分母多项式，并求传递函数的特征根。

解：MATLAB程序代码如下。

  1. num=conv([1,1],conv([1,2,6],[1,2,6]) )  ;%num为分子多项式，conv()函数采用嵌套形式
  2. den=conv([1,0,0],conv([1,3],[1,2,3,4]) );%den为分母多项式，conv()函数采用嵌套形式
  3. r=roots(den);           %r为分母多项式的根

程序运行结果如下：

  1. num =     1     5    20    40    60    36
  2. den =     1     5     9    13    12     0     0
  3. r =       0
  4.           0
  5.          -3.0000
  6.          -1.6506
  7.          -0.1747 + 1.5469i
  8.          -0.1747 - 1.5469i

由计算结果可知，传递函数G(s)的分子多项式为：s5+5s4+20s3+40s2+60s+36；分母多项式为：s6+5s5+9s4+13s3+12s2。

传递函数的分子分母多项式表示形式为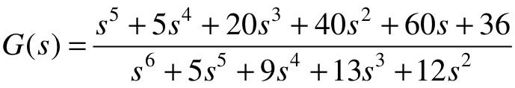：094-2，传递函数的特征根为0、0、-3、-1.6506、-0.1747+1.5469i和-0.1747-1.5469i。

【例4-5】　某一以微分方程描述系统的传递函数，其微分方程描述如下：

094-3

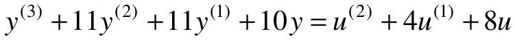
试使用MATLAB建立其模型。

解：建立模型的MATLAB代码如下。

  1. num=[1, 4, 8];  den=[1, 11, 11, 10]    %分子、分母多项式系数行向量
  2. G=tf(num, den)     %建立传递函数模型

程序运行结果如下：

  1.      s^2 + 4 s + 8

s^3 + 11 s^2 + 11 s + 10

从结果可知，系统的传递函数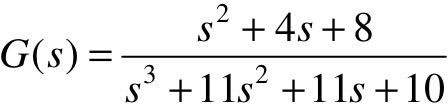094-4。

【例4-6】　已知某系统的传递函数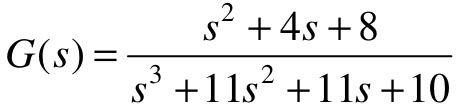094-5，求其分子分母多项式、零极点。

解：MATLAB程序代码如下。

  1. num=[1, 4, 8];  den=[1, 11, 11, 10]  %传递函数分子、分母多项式系数行向量
  2. G=tf(num, den)                       %建立传递函数模型
  3. [tt, ff]=tfdata(G, 'v')              %提取传递函数的分子和分母多项式
  4. [z, p, k]=tf2zp(num, den)            %提取传递函数的零极点和增益

程序运行结果如下：

  1. tt =     0     1     4     8
  2. ff =     1    11    11    10
  3. z =  -2.0000 + 2.0000i        %系统的零点
  4.       -2.0000 - 2.0000i
  5. p =  -10.0000                 %系统的极点
  6.       -0.5000 + 0.8660i
  7.       -0.5000 - 0.8660i
  8. k =     1                     %系统的增益

【例4-7】　已知某系统的传递函数095-1，求其部分分式表示形式。

解：MATLAB程序如下。

  1. num=[2, 0, 9, 1];   den=[1, 1, 4, 4];   %传递函数分子、分母多项式系数行向量
  2. [r, p, k]=residue(num, den)             %求取系统部分分式表示

程序运行结果如下：

  1. r =0.0000 - 0.2500i
  2.    0.0000 + 0.2500i
  3.   -2.0000
  4. p =-0.0000 + 2.0000i
  5.   -0.0000 - 2.0000i
  6.   -1.0000
  7. k =  2

可知结果表达式为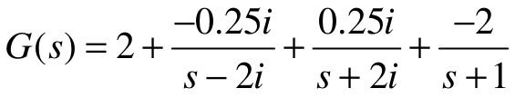：095-2。

【例4-8】　已知某两输入两输出系统的状态方程和输出方程如下：

095-3，求其状态空间模型。

解：MATLAB程序代码如下。

  1. A=[1 6 9 10;3 12 6 8;4 7 9 11;5 12 13 14];B=[4 6;2 4;2 2;1 0];%系统系数矩阵
  2. C=[0 0 2 1;8 0 2 2];  D=zeros(2, 2);     %系统系数矩阵
  3. G=ss(A,B,C, D)                           %生成状态空间模型

程序运行结果如下：

  1. a =   x1  x2  x3  x4
  2.    x1   1   6   9  10
  3.    x2   3  12   6   8
  4.    x3   4   7   9  11
  5.    x4   5  12  13  14
  6. b =   u1  u2
  7.    x1   4   6
  8.    x2   2   4
  9.    x3   2   2
  10.    x4   1   0
  11. c =    x1  x2  x3  x4
  12.    y1   0   0   2   1
  13.    y2   8   0   2   2
  14. d =   u1  u2
  15.    y1   0   0
  16.    y2   0   0

从结果可知，在MATLAB中生成了题中所示的状态空间模型。

【例4-9】　已知单位负反馈系统的开环传递函数为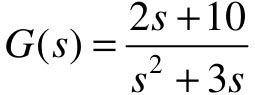096-1，试分别利用Simulink中的传递函数表示模型和零极点表示模型建立整个系统的模型，并将Simulink中的模型转换为状态空间模型。

解：建立Simulink中的传递函数表示模型的基本步骤如下：

（1）利用Simulink的Library窗口中的【File】|【New】，打开一个新的模型窗口。

（2）建立零极点表示的模型，分别从数学运算库（Math）、连续系统库（Continuous）中，用鼠标把传递函数表示模型（Transfer Fcn）、相加器（Sum）标准功能模块选中，并将其拖至模型窗口。

（3）按要求先将前向通道连接好，然后把相加器（Sum）的另一个端口与传递函数和示波器间的线段相连，形成闭环反馈，并将相加器设置为“+-”，形成单位负反馈。

（4）将端口和子系统模块（Ports&Subsystems）中的In输入口模块、Out输出口模块、拖至模型窗口；把In模块作为系统的输入，Out模块作为系统的输出，与系统连接起来。将模型存为“untitled1.mdl”文件。

（5）双击Transfer Fcn，打开其属性设置对话框，并将其中的Numerator（分子多项式表达式系数）设置为“[2 10]”，Denominator（分母多项式表达式系数）设置为“[1 3 0]”，设置的界面及产生的模型如图4.7所示。

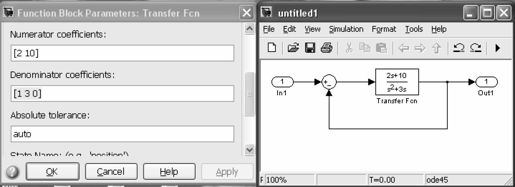
096-01

图4.7　Simulink中的传递函数表示模型及参数设置界面

（6）在MATLAB命令窗口中运行以下命令，得到线性状态空间模型（A, B, C, D）

  1. [A,B,C,D]=[A,B,C,D]=linmod('untitled1');

输出结果为：

  1. A =  -5   -10
  2.      1     0
  3. B =  1
  4.      0
  5. C =  2    10
  6. D =  0

根据题意，系统的开环传递函数的零极点表示形式为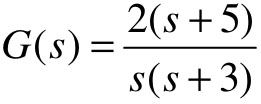097-1，零点为-5；极点为0和-3，增益为2。

建立Simulink中的零极点表示模型的基本步骤如下：

（1）利用Simulink的Library窗口中的【File】|【New】，打开一个新的模型窗口。

（2）建立零极点表示的模型，分别从数学运算库（Math）、连续系统库（Continuous）中，用鼠标把零极点表示模型（Zero-Pole）、相加器（Sum）标准功能模块选中，并将其拖至模型窗口。

（3）按要求先将前向通道连接好，然后把相加器（Sum）的另一个端口与传递函数和示波器间的线段相连，形成闭环反馈，并将相加器设置为“+-”，形成单位负反馈。

（4）将端口和子系统模块（Ports&Subsystems）中的In输入口模块、Out输出口模块、拖至模型窗口；把In模块作为系统的输入，Out模块作为系统的输出，与系统连接起来。将模型存为“untitled1.mdl”文件。

（5）双击零极点表示模型，打开其属性设置对话框，并将其中的Zeros设置为“[-5]”，Poles设置为“[0-3]”，Gain设置为“[2]”，设置的界面及产生的模型如图4.8所示。

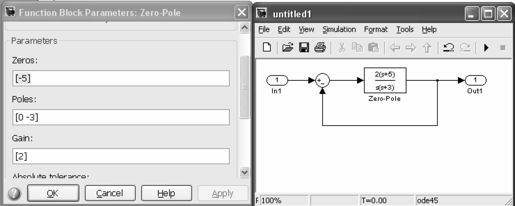
097-01

图4.8　Simulink中的零极点表示模型及参数设置界面