7.6　MATLAB在频率法中的应用

7.6　MATLAB在频率法中的应用
- 7.6.1　求取和绘制频率响应曲线相关的函数
- 7.6.2　应用实例

7.6.1　求取和绘制频率响应曲线相关的函数

MATLAB提供了多种求取并绘制频率响应曲线的函数，如Nyquist曲线绘制函数nyquist( )、Bode图绘制函数bode( )和Nichols曲线绘制函数nichols( )等，下面分别进行介绍。

Nyquist曲线绘制函数nyquist( )

MATLAB提供了绘制系统极坐标图的函数nyquist( )，其用法如下。

nyquist(a, b, c, d)：绘制系统的一组Nyquist曲线，每条曲线对应于连续状态空间系统[a, b, c, d]的输入/输出组合对，其中频率范围由函数自动选取，且在响应快速变化的位置会自动采用更多取样点。
nyquist(a, b, c, d, iu)：绘制从系统第iu个输入到所有输出的极坐标图。
nyquist(num, den)：绘制以连续时间多项式传递函数表示的系统极坐标图。
nyquist(a, b, c, d, iu, w)或nyquist(num, den, w)：利用指定的角频率矢量绘制系统的极坐标图。

当不带返回参数时，直接在屏幕上绘制出系统的极坐标图。

当带输出变量[re, im, w]引用函数时，可得到系统频率特性函数的实部re、虚部im以及角频率点w矢量（为正的部分）；可用plot(re, im)绘制出w从负无穷到零变化的对应部分。

Bode图绘制函数bode( )

MATLAB提供了绘制系统Bode图的函数bode( )，其用法如下。

bode(a, b, c, d)：绘制系统的一组Bode图，它们是针对连续状态空间系统[a, b, c, d]的每个输入的Bode图，其中频率范围由函数自动选取，且在响应快速变化的位置会自动采用更多取样点。
bode(a, b, c, d, iu)：绘制从系统第iu个输入到所有输出的Bode图。
bode(num, den)：绘制以连续时间多项式传递函数表示的系统Bode图。
bode(a, b, c, d, iu, w)或bode(num, den, w)：利用指定的角频率矢量绘制系统的Bode图。

当带输出变量[mag, pha, w]或[mag, pha]引用函数时，可得到系统Bode图相应的幅值mag、相角pha与角频率点w矢量，或只是返回幅值与相角。相角以度为单位，幅值可转换为分贝单位：mag(dB)=20×lg10(mag)。

Nichols曲线绘制函数nichols( )

MATLAB提供了绘制系统的Nichols图的函数nichols ( )，其用法如下。

nichols (a, b, c, d)：绘制系统的一组Nichols图，它们是针对连续状态空间系统[a, b, c, d]的每个输入的Nichols图，其中频率范围由函数自动选取，且在响应快速变化的位置会自动采用更多取样点。
nichols (a, b, c, d, iu)：绘制从系统第iu个输入到所有输出的Nichols图。
nichols (num, den)：绘制以连续时间多项式传递函数表示的系统Nichols图。
nichols (a, b, c, d, iu, w)或nichols (num, den, w)：利用指定的角频率矢量绘制系统的Nichols图。

当带输出变量[mag, pha, w]或[mag, pha]引用函数时，可得到系统Nichols图相应的幅值mag、相角pha与角频率点w矢量，或只是返回幅值与相角。相角以度为单位，幅值可转换为分贝单位：mag(dB)=20×lg10(mag)。

绘制等M圆和等N圆的函数ngrid ( )

MATLAB提供了绘制等M圆和等N圆的函数ngrid( )，ngrid( )对于用nichols函数绘制的Nichols曲线，绘制的相应的等M圆和等N圆，均为虚线圆，并提供有关的对数幅值和相位值。值得注意的是，在对数坐标中，圆的形状发生变化。

ngrid( )的常用的调用格式为：

ngrid('new')：可在绘制网格前清除原图，然后再设置程hold on，这样，后续的nichols函数可与网格绘制在一起。

Nichols图通常与等M圆（等幅值圆）和等N圆（等相角圆）一起使用，从开环频率特性获得闭环频率特性。

7.6.2　应用实例

下面通过实例讲述利用MATLAB来绘制系统的频率响应曲线。

【例7-1】　已知一阶环节传递函数为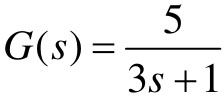 189-1 ，试绘制该环节的Nyquist图。

解：MATLAB程序代码如下。

num=5;  den=[3, 1];  G=tf(num, den)    %建立传递函数模型
nyquist(G); grid                       %绘制Nyquist曲线并添加栅格

输出的Nyquist图如图7.9所示。

190-1

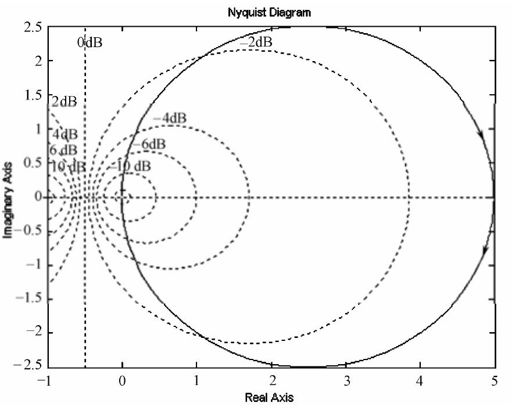
图7.9　例7-1的Nyquist曲线

【例7-2】　已知二阶环节传递函数为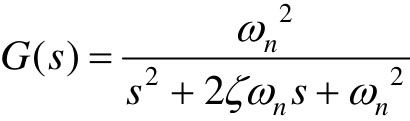 190-2 ，其中ωn=0.7，试分别绘制ζ=0.1, 0.4,1.0,1.6, 2.0时的Bode图。

解：MATLAB程序代码如下。

w=[0, logspace(-2, 2, 200)]     %w为10-2～10-2之间对数等间距分布的200个数
wn=0.7                          %自然振荡角频率
tou=[0.1, 0.4, 1.0, 1.6, 2.0]   %阻尼比的不同取值
for j=1:5
sys=tf([wn*wn], [1, 2*tou(j)*wn, wn*wn]) %不同阻尼比下的系统传递函数
bode(sys, w);  hold on;         %绘制Bode图
end
%放置tou取不同值的文字注释
gtext('tou=0.1'); gtext('tou=0.4'); gtext('tou=1.0'); gtext('tou=1.6'); gtext('tou=2.0')

输出的Bode图如图7.10所示。

190-3

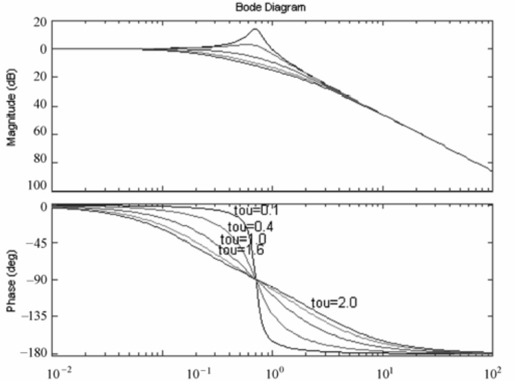
图7.10例7-2的二阶系统Bode图

【例7-3】　已知一高阶系统的传递函数为 191-1 ，试绘制系统的Nichols图。

解：MATLAB程序代码如下。

num=[0.0001, 0.0281, 1.06356, 9.6];    %传递函数分子多项式系数行向量
den=[0.0006, 0.0286, 0.06356, 6]       %传递函数分母多项式系数行向量
G=tf(num, den)                         %建立传递函数模型
ngrid('new')                           %绘制等M圆和等N圆
nichols(G)                             %绘制系统的Nichols图

输出的Nichols图如图7.11所示。

191-2

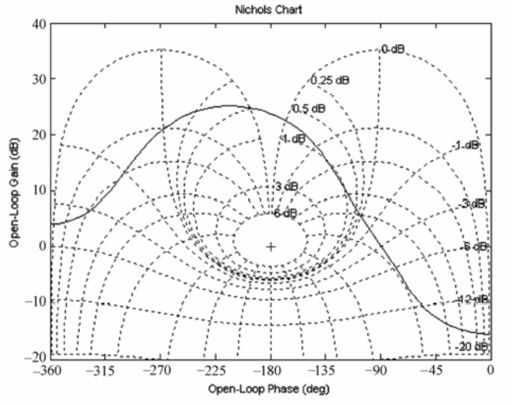
图7.11　例7-3高阶系统Nichols图

【例7-4】　已知二阶系统的传递函数为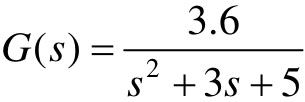 191-3 ，试计算此系统的谐振幅值和谐振频率。

解：计算谐振幅值和谐振频率的MATLAB程序代码如下。

function [Mr, Pr, Wr]=mr(G)
[mag, pha, w]=bode(G)    %得到系统Bode图相应的幅值mag、相角 pha与角频率点w矢量
magn(1, :)=mag(1, :); phase(1, :)=pha(1, :)
[M, i]=max(magn)
Mr=20*log10(M)           %求得谐振峰值
Pr=phase(1, i)
Wr=w(i, 1)               %求得谐振频率

主函数的MATLAB程序代码如下。

num=[3.6]; den=[1, 3, 5];  G=tf(num, den)   %建立传递函数
[Mr, Pr, Wr]=mr(G)         %求取谐振幅值和谐振频率

程序运行结果如下：

Mr = -2.8098
Pr = -24.6446
Wr =  0.6915

由运行结果可知，系统的谐振峰值Mr=-2.8098dB，谐振频率ωr=0.6915rad/s。

还可以从MATLAB绘制的频率响应曲线上直接得到谐振峰值和谐振频率。步骤是先生成频率响应曲线，然后在频率响应图内部空白处用鼠标右键单击，弹出菜单，选择“Peak Response”菜单项，将在频率响应图上出现一个圆点，该点就是系统的谐振频率处。

例7-4绘制Bode图的MATLAB程序代码如下：

num=[3.6]; den=[1, 3, 5] ;  G=tf(num, den)   %建立传递函数
bode(G)             %绘制Bode图

程序输出如图7.12所示的Bode图（图中的弹出菜单非Bode图内容，作用见下）。

192-1

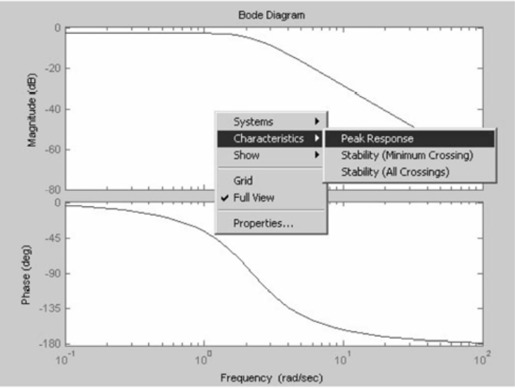
图7.12　例7-4系统Bode图

单击鼠标右键，弹出菜单，选择“Peak Response”菜单项，将光标移至圆点处，输出如图7.13所示的图形。

192-2

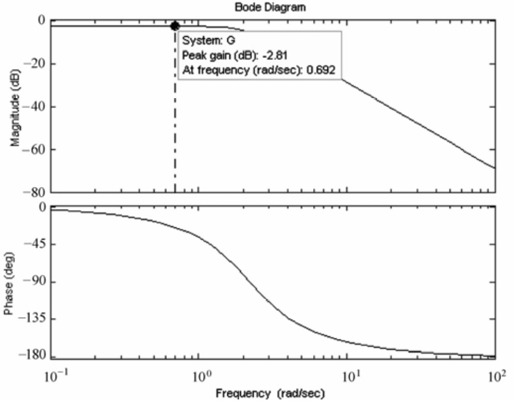
图7.13　例7-4系统Bode图（显示谐振峰值和谐振频率）

从图中可以看出，系统的谐振峰值Mr=-2.81 dB，谐振频率ωr=0.692 rad/s，与前面的计算结果是一致的。

也可以用同样的方法直接从MATLAB绘制的Nyquist图和Nichols图中得到谐振峰值和谐振频率。

7.6 MATLAB在频率法中的应用