7.8　综合实例及MATLAB/Simulink应用

下面通过一个综合实例，讲述MATLAB/Simulink在本章中的应用。

【例7-9】　已知晶闸管－直流电机开环系统的结构图如图7.23所示。试用Simukink动态结构图进行频域分析并求频域性能指标。

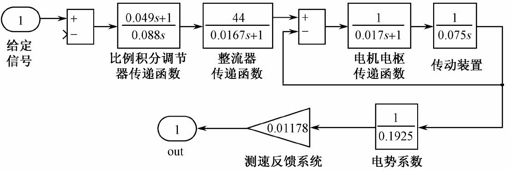
图7.23　系统结构图

解：利用Simulink求解的基本步骤如下。

【步骤1】　在Simulink中建立该系统的动态模型，如图7.24所示。

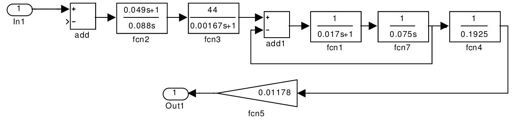
图7.24　Simulink中的系统动态模型

并将模型存为“Samples_7_9.mdl”。

【步骤2】　求取系统的线性状态空间模型，并求取频域性能指标。

在MATLAB命令窗口中运行以下命令：

[A,B,C,D]=linmod('Samples_7_9');     %提取Simulink模型的线性状态空间模型
sys=ss(A,B,C,D);
margin(sys);                         %求取频域指标

程序运行后，输出如图7.25所示。

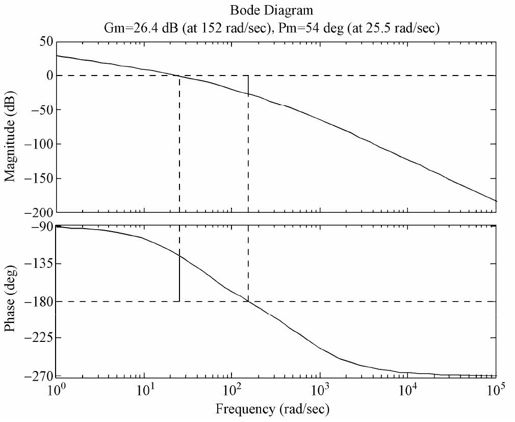
图7.25　系统的开环Bode图和频域性能指标

从图中可以看出：

• 幅值裕度GM=26.4dB，穿越频率为152 rad/sec；
• 相位裕度PM=54 deg，穿越频率为25.5 rad/sec。

习　题

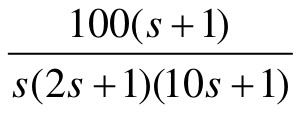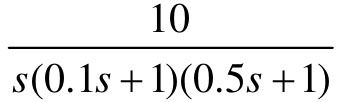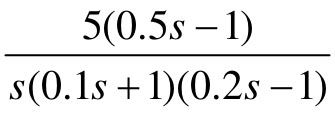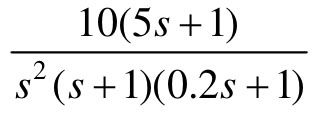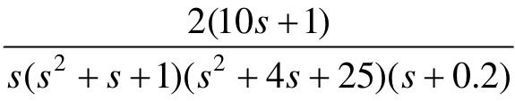【7.1】　给定控制系统的开环传递函数G(s)分别为、、、和，试用MATLAB分别绘制其幅频特性曲线和Nyquist曲线，并判断闭环系统的稳定性。

【7.2】　已知单位负反馈控制系统的开环传递函数G(s)分别为和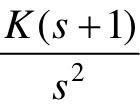。试分析系统增益K对相角裕量的影响。

【7.3】　某控制系统结构如图7.A所示。

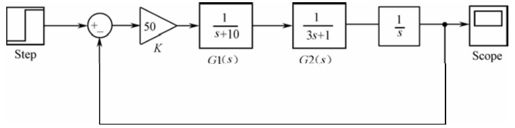
图7.A　习题

（1）利用MATLAB建立图示控制系统的数学模型；

（2）绘制开环系统的Bode曲线和Nyquist曲线；

（3）判断系统的稳定性，如果不稳定，绘制闭环系统的零极点图，给出极点的位置；

（4）计算系统的截止角频率、相角裕量和幅值裕量；

（5）绘制系统的阶跃响应曲线。

【7.4】　设单位负反馈控制系统的开环传递函数G(s)为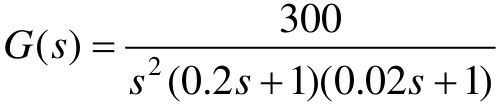

（1）利用MATLAB建立上述控制系统的数学模型；

（2）使用MATLAB中的margin命令，绘制系统的Bode图，分析系统的稳定性，并读出幅值穿越频率的值。

【7.5】　给定单位负反馈控制系统的开环传递函数G(s)分别为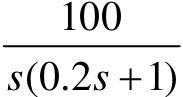、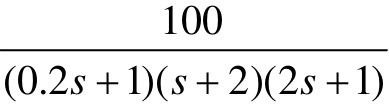和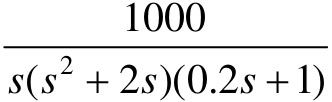，试利用LTI Viewer工具，分别绘制其Bode图和Nyquist曲线，判断系统的稳定性。如果系统稳定，利用margin命令计算系统的相角裕量和增益裕量。

【7.6】　设单位负反馈控制系统的开环传递函数G(s)分别为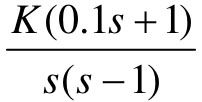、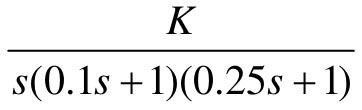和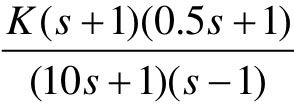，试绘制其Nyquist曲线，并确定使闭环系统稳定的K的取值范围。

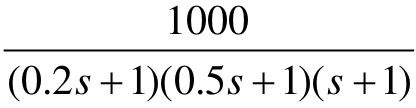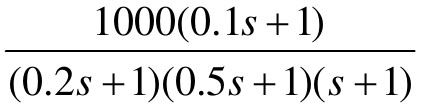
【7.7】　设单位负反馈控制系统的开环传递函数G(s)分别为、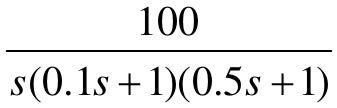和，试绘制其Nyquist曲线，判断闭环系统的稳定性。对于闭环不稳定的系统，通过Nyquist曲线得出位于S右半平面的闭环极点个数。

【7.8】　已知控制系统的开环传递函数为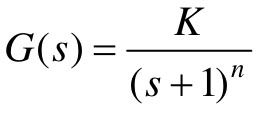

（1）利用MATLAB验证：当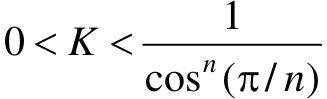时，闭环系统稳定；

（2）选定几组符合上述条件的n和K，绘制系统的阶跃响应曲线。