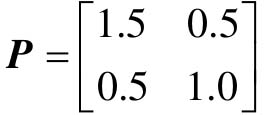9.4　线性系统稳定性分析

9.4.1　稳定性分析基础

对于一个实际的控制系统，其工作的稳定性无疑是一个极其重要的问题，一个不稳定的系统在实际应用中是很难有效发挥作用的。

从直观上看，系统的稳定性就是指一个处于稳态的系统，在某一干扰信号的作用下，其状态偏离了原有平衡位置，若系统是稳定的，那么在干扰取消后的有限时间内，系统会在自身作用下回到平衡状态；反之若系统不稳定，则系统永远不会回到原来的平衡位置。

系统的稳定分外部稳定和内部稳定两种：外部稳定又称为输出稳定，也就是系统在干扰取消后，在一定时间内其输出会恢复到原来的稳态输出，输出稳定有时描述为系统的BIBO稳定，即有限的系统输入只能产生有限的系统输出；系统内部稳定主要针对系统内部状态，反映的是系统内部状态受干扰信号的影响情况，当干扰信号取消后，若系统的内部状态会在一定时间内恢复到原来的平衡状态，则称系统状态是稳定的。

在经典控制论中，研究对象都是用高阶微分方程或传递函数描述的单输入单输出（SISO）系统，反映的仅是输入与输出的关系，不涉及系统的内部状态，因此经典控制论中只讨论系统的输出稳定问题。

系统的稳定性是系统本身的特性，与系统的外部输入（控制）无关。

如果系统不是线性定常系统，那么对于系统内部状态稳定问题，经典控制论中的方法就不好发挥作用了，这就需要用到下面介绍的李雅普诺夫（Lyapunov）稳定性理论。

设控制系统的齐次状态方程为

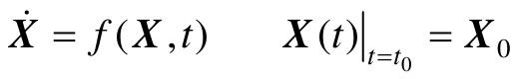
其中，X(t)为系统的n维状态向量，f是有关状态向量X以及时间t的n维矢量函数，f不一定是线性定常的。如果对于所有t，状态Xe总满足：f(Xe,t)=0，则称Xe为系统的平衡状态。对于一般控制系统，可能没有，也可能有一个或多个平衡状态。

如果系统是一个线性定常系统，即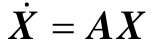，那么当A为非奇异矩阵时，Xe=0是系统的唯一平衡状态；当A为奇异矩阵时，AX=0有无数解，也就是说系统有无数个平衡状态。

系统的状态稳定性是针对系统的平衡状态的，当系统有多个平衡状态时，需要对每个平衡状态分别进行讨论。对系统矩阵A非奇异的线性定常系统，Xe=0是系统的唯一平衡状态，所以对线性定常（LTI）系统，一般可笼统地用Xe的稳定性代表系统的稳定性。

9.4.2　李雅普诺夫稳定性分析

1892年，李雅普诺夫就如何判断系统的稳定性问题归纳出两种方法（称为第一法和第二法），第一法的基本思路和分析方法与经典控制理论是一致的；第二法的特点是不求解系统方程，而是通过一个叫李雅普诺夫函数的标量函数来直接判断系统的稳定性。

9.4.2.1　李雅普诺夫稳定性定义

设一般控制系统的解为：X(t)=Φ(t;X0,t0)，它是与初始时间t0及其初始状态X0有关的，体现系统状态从(t0,X0)出发的一条状态轨迹。

设Xe为系统的一个平衡点，如果给定一个以Xe为球心，以ε为半径的n维球域S(ε)，总能找到一个同样以Xe为球心，δ(ε,t0)为半径的n维球域S(δ)，使得从S(δ)球域出发的任意一条系统状态轨迹Φ(t;X0,t0)在t≥t0的所有时间内，都不会跑出S(ε)球域，则称系统的平衡状态Xe是李雅普诺夫稳定的（Lyapunov Stability）。

一般来说，δ的大小不但与ε有关，而且与系统的初始时间t0有关。当δ仅与ε有关时，称Xe是一致稳定的平衡状态。

进一步地，如果Xe不仅是李雅普诺夫稳定的平衡状态，而且当时间t无限增加时，从S(δ)球域出发的任一条状态轨迹Φ(t;X0,t0)都最终收敛于球心平衡点Xe，那么称Xe是渐进稳定的（Asymptotic Stability）。

更进一步，如果从S(∞)即整个系统状态空间的任一点出发的任一条状态轨迹Φ(t;X0,t0)，当t→∞时都收敛于平衡点Xe，那么称Xe是大范围渐进稳定的。显然，此时的Xe是系统的唯一平衡点。

反之，对于给定S(ε)，不论δ>0取得多么小，若从S(δ)球域出发的状态轨迹Φ(t;X0,t0)至少有一条跑出S(ε)球域，那么称平衡点Xe是不稳定的。

9.4.2.2　李雅普诺夫第一法（间接法）

李雅普诺夫第一法通过分析系统微分方程的显式解来分析系统的稳定性，对线性定常系统，它可以直接通过系统的特征根来分析。李雅普诺夫第一法的基本思路与经典控制论中的稳定性判别思路基本一致。

设线性定常系统的动态方程为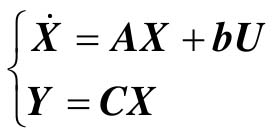，在讨论系统状态稳定性（内部稳定）时，可以不考虑系统的输入结构和输入信号，而只考虑系统的齐次状态方程或矩阵A，显然，当|A|≠0时，Xe=0是系统的惟一平衡点。

对于Xe=0的稳定性，有如下判据（Xe大范围渐进稳定的充分必要条件）。

当线性定常系统的系统矩阵A的所有特征根都有负的实部时，其惟一的状态平衡点Xe=0是渐进稳定的，而且是大范围渐进稳定的。

对于线性定常系统，其输入/输出的传递函数为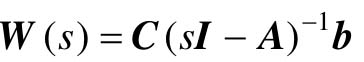，当W(s)的极点全部都有负实部时，该系统有界的输入将引起有界的输出（BIBO），也就是说系统是输出稳定的。

可以证明，当系统的传递函数W(s)没有零极点对消时，系统的状态稳定性和系统的输出稳定性是一致的，因为此时系统矩阵的特征根就是系统传递函数的极点。

9.4.2.3　李雅普诺夫第二法（直接法）

李雅普诺夫第二法不必求解系统的状态方程，而是通过一个系统的能量函数来直接判断系统的稳定性，所以又称为直接法。直接法不但适用于线性定常系统，而且适用于非线性和时变的系统。

在实际系统中，往往不容易找出系统的能量函数，于是李雅普诺夫定义了一个正定的标量函数V(x)，作为系统的虚构广义能量函数。根据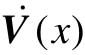的符号性质，可以判断系统的状态稳定性。

设V(x)是定义在n维空间Rn上的标量函数，且当X=0时，V(x)=0，那么对其余X∈Rn3，有

• 若V(x)>0，则称V(x)是正定的；
• 若V(x)≥0，则称V(x)是半正定的（非负定）；
• 若V(x)<0，称V(x)是负定的；
• 若V(x)≤0，则称V(x)是半负定的（非正定）；
• 若V(x)任意，则称V(x)不定。

在建立于李雅普诺夫第二法基础上的稳定性分析中，有一类标量函数起着重要的作用，它就是二次型函数。

设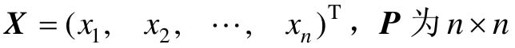阶的实对称矩阵，则

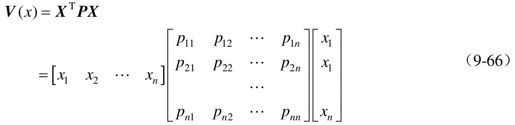
称为二次型函数。

二次型标量函数的符号性质可以由赛尔维斯特（Sylvester）准则来判别。设实对称阵P的各阶主子行列式为

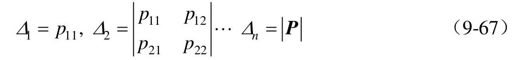
（1）若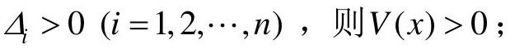

（2）若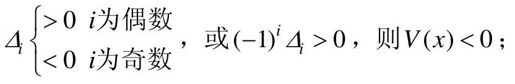

（3）若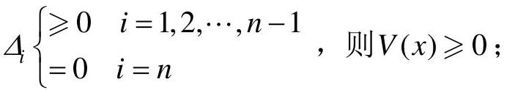

（4）若

设系统状态方程为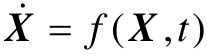：，其中，Xe=0为系统的一个平衡状态。

如果存在一个正定的标量函数V(x)，并且具有连续的一阶偏导数，那么根据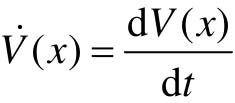的符号性质，有：

应当指出，上述稳定性判据只是一个充分条件，并不是必要条件。如果给定的V(x)满足上述4个条件之一，那么其结果成立。反之，如果给定的V(x)不满足上述任何一个条件，那么只能说明所选的V(x)对式（9-157）所表示的系统失效，必须重新构造V(x)。

9.4.2.4　线性定常系统的李雅普诺夫稳定分析及系统参数优化

研究下列线性定常系统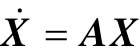：，若A为非奇异矩阵，那么Xe=0是系统的惟一平衡状态，其稳定性可以通过李雅普诺夫第二法来分析。取

式中，P为正定实对称矩阵，所以V(x)对X有连续偏导数，并且V(x)>0。

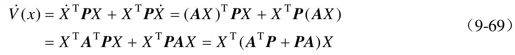
令

式（9-70）称为李雅普诺夫方程，可得

式中，Q=-(ATP+PA)为对称矩阵。若Q>0，则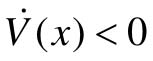，因此Xe=0为渐进稳定，而且是大范围渐进稳定。

在实际应用中，先给定一正定矩阵Q，然后通过李雅普诺夫方程求出实对称矩阵P，最后通过赛尔维斯特准则判别P的正定性。若P>0，则系统稳定。

在应用李雅普诺夫方程时，应注意以下几点：

（1）由李雅普诺夫方程求得的P为正定是Xe=0渐进稳定的充分必要条件。

（2）Q的选取是任意的，只要满足对称且正定（在一定条件下可以是半正定），Q的选取不会影响系统稳定性判别的结果。

（3）如果ai(t)沿任意一条轨迹不恒等于零，那么Q可以取半正定阵，即Q≥0。

（4）当Q取为单位阵I时，李雅普诺夫方程变为：ATP+PA=-I，这是一个比较简单的李雅普诺夫方程。

9.4.3　MATLAB/Simulink在李雅普诺夫稳定性分析中的应用

在MATLAB控制工具箱中，提供了求解李雅普诺夫方程的函数lyap( )、lyap2( )和dlyap( )，函数常用的调用格式如下：

P=lyap(A, Q)，其中输入参数A是已知系统的状态矩阵，Q是给定的正定对称矩阵，输出量P是李雅普诺夫方程AP+PAT+Q=0的解，即正定实对称矩阵P。

P=lyap2(A, Q)，其中输入参数A是已知系统的状态矩阵，Q是给定的正定对称矩阵，输出量P是李雅普诺夫方程AP+PAT+Q=0的解，即正定实对称矩阵P。lyap2( )采用特征值分解法求解李雅普诺夫方程，其运算速度比lyap( )快很多。

对于离散系统，相应的函数为P=dlyap(A, Q)，参数的含义与连续系统的类似，此处不再赘述。

【例9-12】　已知系统的状态矩阵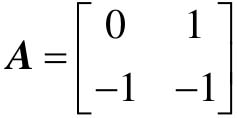，给定的正定对称矩阵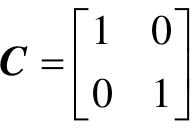，试求李雅普诺夫方程的解P。

解：MATLAB程序代码如下。

A=[0, 1; -1, -1];     %状态矩阵
Q=[1, 0; 0, 1];      %给定的正定对称矩阵
P=lyap(A', Q);      %求解李雅普诺夫方程

运行结果如下：

P= 1.5000  0.5000
    0.5000  1.0000

由运算结果可知，李雅普诺夫方程的解