11.2 非线性系统概述
11.2.1 非线性控制理论发展概况
在控制领域,人们最先研究的控制系统都是线性的。对线性系统的物理描述和数学求解是比较容易实现的事情,而且已经形成了一套完善的线性理论和分析研究方法。但对非线性系统来说,除极少数情况外,目前还没有一套可行的通用方法,而且每种方法只能适用于某一类问题,不能普遍适用。
目前对非线性系统的认识和处理基本上还是处于初级阶段。另一方面,从对控制系统的精度要求来看,用线性系统理论来处理目前绝大多数工程技术问题在一定范围内都可以得到比较满意的结果,因此,一个物理系统的非线性因素常常被忽略了,或者被各种线性关系所简化或代替。这就是线性系统理论发展迅速并趋于完善,而非线性系统理论长期得不到重视和发展的主要原因。
随着科学技术的不断发展,人们对实际生产过程的分析要求日益精密,各种较为精确的分析和科学实验结果表明,任何一个实际的物理系统都是非线性的。所谓线性只是对非线性的一种简化或近似,或者说是非线性的一种特例。
到20世纪40年代,对非线性系统的研究已取得一些明显的进展。目前主要的非线性分析方法有相平面法、李亚普诺夫法和描述函数法等,这些方法都已经被广泛用来解决实际的非线性系统问题。
但是这些方法都有一定的局限性,都不能成为分析非线性系统的通用方法。例如,用相平面法虽然能够获得系统的全部特征,如稳定性、过渡过程等,但对于大于三阶的系统则无法应用。李亚普诺夫法仅限于分析系统的绝对稳定性问题,而且要求非线性元件的特性满足一定条件。虽然这些年来,国内外有不少学者一直在这方面进行探讨,也研究出了一些新的方法,如频域的波波夫判据、广义圆判据、输入/输出稳定性理论等,但总的来说,非线性控制系统理论目前仍处于发展阶段,远非线性系统那样完善,很多问题都还有待解决,未来的研究领域十分宽广。
11.2.2 典型非线性特性
含有非线性元件或环节的系统称为非线性系统。非线性特性包括许多类型,典型的静态非线性特性包括死区非线性、饱和非线性、间隙非线性和继电非线性,下面分别加以介绍。
11.2.2.1 死区非线性
死区非线性是一种常见的非线性,如图11.1所示,它通常是由放大器、传感器、执行机构的不灵敏区造成的。
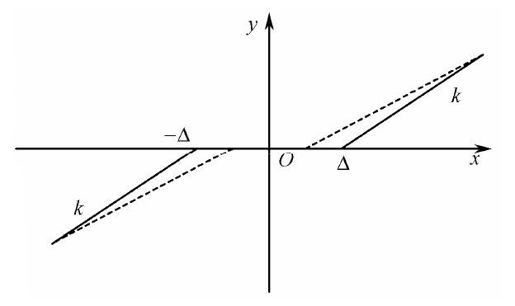
图11.1 死区非线性
理想的死区非线性一般可用图11.1中的三段直线(实线)来表示;实际的死区非线性一般可用图11.1中的点画线来表示。理想的死区非线性可用数学模型描述为

从式(11-1)可以看出,当输入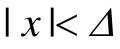 时,输出为0,系统处于开环状态,失去调节作用,控制灵敏度下降,稳态误差加大,给控制系统带来不利影响;另一方面,当系统输入端存在小扰动信号时,死区可减小扰动信号,给控制系统带来有利影响,有些系统为提高抗干扰能力而引入死区非线性。就静态特性而言,死区非线性总是增大系统稳态误差。
时,输出为0,系统处于开环状态,失去调节作用,控制灵敏度下降,稳态误差加大,给控制系统带来不利影响;另一方面,当系统输入端存在小扰动信号时,死区可减小扰动信号,给控制系统带来有利影响,有些系统为提高抗干扰能力而引入死区非线性。就静态特性而言,死区非线性总是增大系统稳态误差。
11.2.2.2 饱和非线性
饱和非线性如图11.2所示,它是由饱和引起的。当输入增大到某个值以后,输出便不再变化,这种现象称为饱和。任何实际的控制系统都存在饱和非线性,因为其输出不可能无限增大,这是放大元件或执行元件的固有特性。
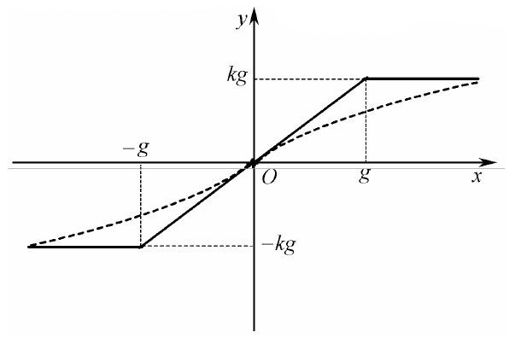
图11.2 饱和非线性
理想的饱和非线性一般可用图11.2中的三段直线来表示;实际的饱和非线性一般可用图11.2中的点划线表示。理想的饱和非线性特性可用数学模型描述为:

饱和非线性往往促使系统稳定,但会减小放大系数,因而降低稳态精度。有时出于技术上的考虑,采用限幅,以使特性的线性区变窄,实际上是利用了饱和非线性。
11.2.2.3 间隙非线性
间隙非线性如图11.3所示,其形成原因通常是由于滞后的作用,类似于线性系统的滞后环节,但不完全等价。齿轮传动是典型的间隙非线性。
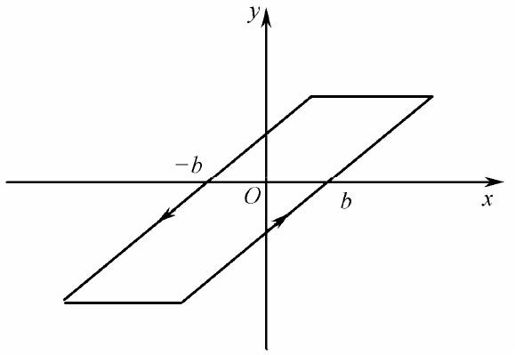
图11.3 间隙非线性
间隙非线性可用数学模型描述为
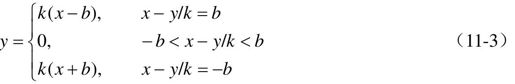
间隙非线性对控制总是有害的,它会引起系统不稳定或自激振荡,对系统稳定品质也不利,故应消除或削弱它的影响。
11.2.2.4 继电非线性
继电非线性顾名思义就是继电器所具有的非线性,其他装置(如电磁阀、斯密特触发器等)都具有类似的非线性特性。它常见的种类有双位继电非线性,如图11.4(a)所示,以及三位继电非线性,如图11.4(b)所示。
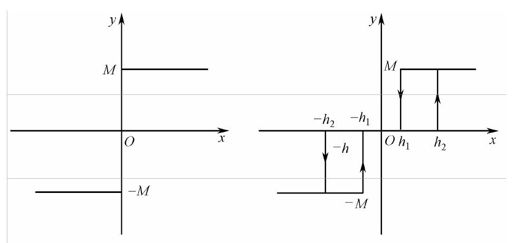
图11.4 继电非线性
双位继电非线性可用数学模型描述为

三位继电非线性(b)可用数学模型描述为
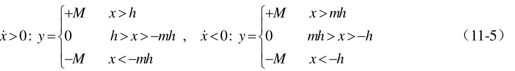
继电非线性常会使系统产生振荡,对系统是不利的。分析继电非线性具有十分重要的意义,因为采用继电器、电磁阀等元件的控制系统比比皆是,例如大多数家用电冰箱、空调就属于继电器控制系统,研究继电非线性的目的就是为了克服其不利影响,最终使具有继电非线性的控制系统更加完善。
11.2.3 Simulink中的非线性模块
Simulink中的不连续系统模块库(Discontinuous)提供了12种常用标准非线性模块,如回环、死区、继电器、饱和、开关等非线性模块。
对非线性系统进行仿真时,可直接调用这些非线性模块,从而省去了编程实现这些非线性特性的麻烦。当然,对于那些Simulink中没有提供的非线性模块,则需要根据具体的非线性特性来编程实现,然后封装成模块,仿真时就可以直接调用了。
在Simulink基本模块中选择不连续系统模块库后,单击便看到如图11.5所示的界面。
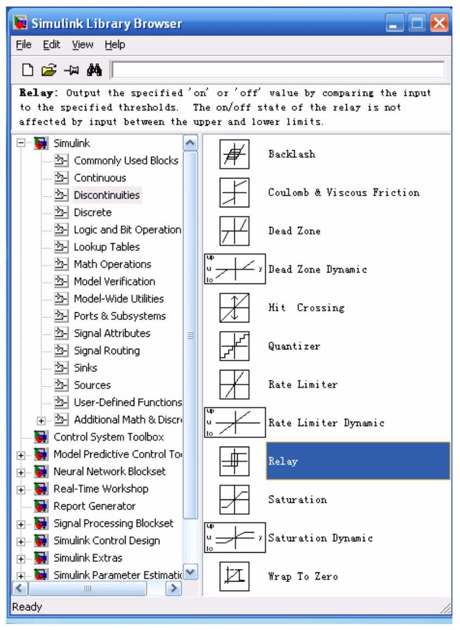
图11.5 Simulink中的非线性模块窗口
从图11.5中可以看出,不连续系统模块库包括以下非线性模块。
- Backlash:间隙非线性;
- Coulomb&Viscous Friction:库仑和黏度摩擦非线性;
- Dead Zone:死区非线性;
- Dead Zone Dynamic:动态死区非线性;
- Hit Crossing:冲击非线性;
- Quantizer:量化非线性;
- Rate Limiter:比例限制非线性;
- Rate Limiter Dynamic:动态比例限制非线性;
- Relay:继电非线性;
- Saturation:饱和非线性;
- Saturation Dynamic:动态饱和非线性;
- Wrap To Zero:环零非线性。
需要注意的是,这些模块的框图,表示了次非线性特性的输入和输出的关系,例如,死区非线性的框图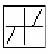 ,它与图11.1描述的输入和输出关系相似,因此,从框图上便可直接看出其输入和输出关系。
,它与图11.1描述的输入和输出关系相似,因此,从框图上便可直接看出其输入和输出关系。
单击模块时,在上方的框中将出现关于此非线性特性的介绍。
【例11-1】 死区非线性的输入和输出特性实例。在Simulink中,利用幅值为1的正弦信号直接作用于限幅为0.5的死区非线性模块,试求其输出,并与输入信号进行比较。
解:具体步骤如下:
(1)在Simulink的Library窗口中选择【File】|【New】,建立一个新的Simulink工作平台;
(2)分别将信号源库、输出方式库、信号路线和非线性环节库中的Sine、Scope、Mux和Dead Zone各功能模块拖至工作平台;
(3)按系统要求将各模块加以连接,如图11.6所示,并对各模块进行参数设置,如设置死区非线性模块的Start of dead zone为-0.5,End of dead zone为0.5;
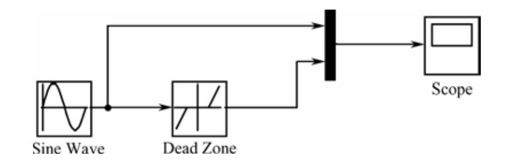
图11.6 正弦信号作用于死区非线性正弦信号对比图
(4)执行仿真,双击Scope图标可得到系统的仿真曲线如图11.7所示,图中可以清晰看出原始信号(幅值为1的正弦信号)和死区非线性作用后的曲线。
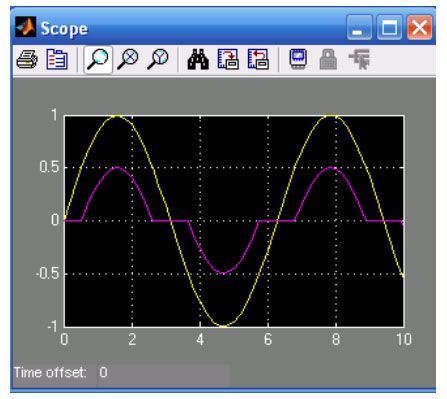
图11.7 死区非线性模块作用前后的标准模块的模型
读者可以利用类似的方法,通过Simulink方便地研究其他非线性特性,例如,在分析库仑和黏度摩擦非线性时,可建立类似于上例的系统,然后仿真,对比分析次非线性特性。模型和仿真结果如图11.8所示,具体分析过程此处不再赘述。
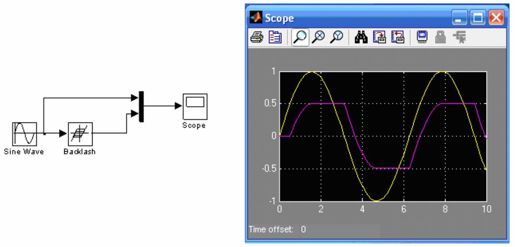
图11.8 库仑和黏度摩擦非线性特性的Simulink简单仿真分析
