11.3　相平面法

相平面法是庞加莱（Poincare）于1885年首先提出的，它通过图解法把求解一阶和二阶系统运动方程组转化成位置和速度平面上的相轨迹，能直观、准确地反映系统的稳定性、平衡状态和稳态精度以及初始条件和参数对系统运动的影响。

应用相平面法分析一阶尤其是二阶非线性控制系统，弄清非线性系统的稳定性、稳定域等基本属性以及解释极限环等特殊现象，具有非常直观形象的效果。

由于绘制二维以上的相轨迹十分困难，因此相平面法对于二阶以上的系统几乎无能为力，这是相平面法的局限。

11.3.1　相平面法基础知识

11.3.1.1　相轨迹和相平面

对于二阶时不变系统可用式（11-6）所示的常微分方程描述，有

式中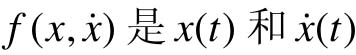，的线性或非线性函数。该方程的解可以用x(t)的时间函数曲线表示。

把式（11-6）所示的二阶微分方程改写成二元一阶微分方程组，有

式中，x可以看成广义位移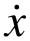，可以看成广义速度。对式（11-7）所示的微分方程组求解，可以得到解。

如果取x(t)为横坐标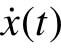，为纵坐标，以时间t为参变量，就可以用x(t)和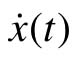的关系曲线表示方程的解，而t为参变量。此时，系统每一时刻的状态均对应于该平面上的一点，当参变量t变化时，方程的解在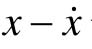平面上绘出的曲线即表征了系统的运动过程，这个曲线就是相轨迹。相轨迹上箭头符号表示参变量时间t的增加方向。两个变量构成的直角坐标系称为相平面。

根据微分方程解的存在与唯一性定理，对于任一给定的初始条件，相平面上有一条相轨迹与之对应。多个初始条件下的运动对应多条相轨迹，形成相轨迹簇，而由一簇相轨迹所组成的图形称为相平面图。

11.3.1.2　奇点

对于二阶系统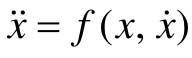，相平面上满足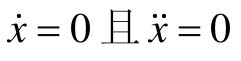的点叫做奇点，记为Xe。奇点坐标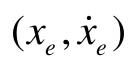是下列代数方程的解，显然奇点一定在坐标轴上。

对于二阶系统，表示系统的“速度”和“加速度”均为零，也就意味着系统不再运动，因此，奇点又称为平衡点。相平面上任何其他点都叫普通点。奇点又分稳定奇点和不稳定奇点。

11.3.1.3　相轨迹切线斜率

由式（11-7）可知，相轨迹上任一点的切线斜率为

某点的切线斜率就是相轨迹通过该点的运动方向。

在奇点处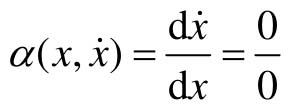，，其值不定，表明系统在奇点处可以按任意方向趋近或离开奇点，因此，在奇点处多条相轨迹相交。

等倾线就是相轨迹场上所有切线斜率等于某一常数的点的连线。

11.3.1.4　相轨迹图形特征

如果微分方程（11-7）满足解的存在性和唯一性条件，那么相轨迹图一定有如下基本特征：

（1）相轨迹不相交，即相平面上任一普通点有且只有一条相轨迹通过（坐标原点除外）；

（2）相轨迹必垂直通过坐标轴；

（3）相平面横轴上方的相轨迹从左向右运动，横轴下方的相轨迹从右向左运动。

11.3.1.5　极限环

极限环是非线性系统特有的现象，它对应的响应曲线是等幅振荡，也是一种随处可见的现象，可以说，凡是能持续振荡的动态系统都是运行在稳定极限环上的。钟摆的摆动、电子振荡器等都是例证。显然，在干扰环境中，线性系统不可能产生持续等幅振荡，因为极微小的干扰就可能导致振荡发散或衰减到零。

极微小的干扰就导致系统振荡发散或衰减到零的极限环称为不稳定极限环。即使干扰使振荡短时离开极限环，干扰消失后则又回到的极限环称为稳定极限环。

11.3.2　MATLAB/Simulink在相轨迹图绘制中的应用

相轨迹图有多种绘制办法，主要有以下3种：

（1）手工绘制概略图。概略图就像相轨迹的“素描”，它是根据相轨迹的基本特征、特殊点、特殊线等信息而“随手”画出的草图，它虽然在具体细节上缺乏精度，但能提供许多重要的定性结论。

（2）手工绘制近似图。在计算机未得到广泛应用的年代，人们研究出好几种手工近似作图法，如等倾线法、δ法等。这些手工作图法要绘出有一定精度的相轨迹图是十分烦琐的，如今已没有多大实用价值。

（3）计算机绘制精确图。借助计算机数值解法以及MATLAB/Simulink等软件绘制相轨迹图。

下面讲述采用MATLAB/Simulink绘制相轨迹图的方法。

11.3.2.1　采用MATLAB绘制相轨迹图

绘制相轨迹图的实质是求解微分方程的解。求解微分方程数值解的算法有多种，MATLAB提供了求解微分方程的函数组，常用的有ode45，它采用的计算方法是变步长的龙格-库塔4/5阶算法。

ode45()常用的调用格式如下：

[t, y]=ode45(odefun, tspan, y0)

在用户自己编写的MATLAB函数中既可以描述线性系统特性，也可以描述非线性系统特性。描述系统模型的文件名可以由字符串变量名odefun给出；参数tspan可以由初始时间t0和终止时间tfinal构成向量给出，如tspan=[t0 tfinal]，参数y0为系统状态变量初始值，其默认值是一个空矩阵。函数调用后，将返回系统的时间向量t和状态变量y。

【例11-2】　已知一个二阶线性系统的微分方程为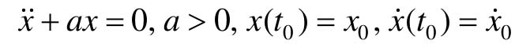：，其中a=2，试用MATLAB函数绘制系统的相平面图和零输入响应曲线。

解：取状态变量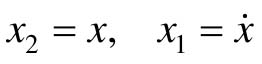，得到系统状态方程模型，即一阶常微分方程组：

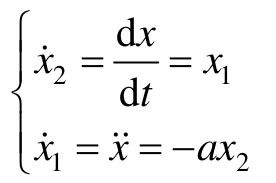
由此模型就可以用MATLAB来求解了。

主程序MATLAB代码如下：

% test_11_2是系统微分方程的描述函数
  [t, x]=ode45('test_11_2', [0, 20], [0, 1]);     %初始化状态变量为[0, 1]，计算时间为[0, 20]
  [t1, x1]=ode45('test_11_2', [0, 20], [1, 1]);      %初始化状态变量为[1, 1]，计算时间为[0, 20]
plot(x(:, 1), x(:, 2), '-', x1(:, 1), x1(:, 2), '.');        %绘制相轨迹
xlabel('x'); ylabel('dx/dt')        %添加横纵坐标标注
grid               %添加栅格
title('相轨迹图')      %添加图表题

运行结果如下：

%例11-2程序的子函数代码
function xdot= test_11_2(t, x)        %求取状态导数的函数
xdot=[-2*x(2); x(1)];     %导数关系式
%格式
%  function xdot=filename(t, x)
%  xdot=[表达式1；表达式2；表达式3；…；表达式n-1]
%  表达式1 对应  x1'=x2;  表达式2 对应  x2'=x3
%  表达式3 对应  x3'=x4; …；表达式n-1对应  xn-1'=xn

主函数运行后，输出如图11.9所示的相轨迹图。

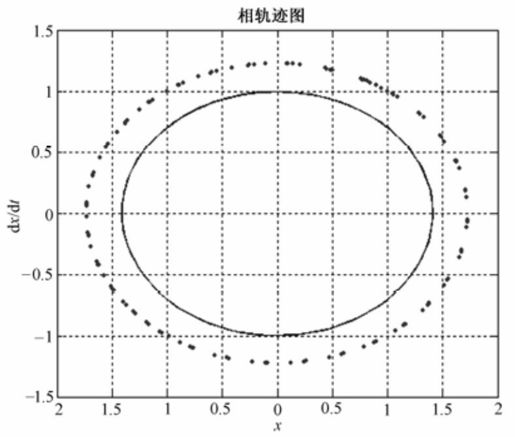
图11.9　例11-2相轨迹图

然后输入如下MATLAB程序代码来绘制系统时域响应图：

plot(t, x(:, 2), '-', t1, x1(:, 2), '.')       %绘制时域响应曲线
xlabel('t');   ylabel('x(t)')        %添加横纵坐标标注
grid          %添加栅格
title('时间响应曲线')       %添加图表题

运行后，输出如图11.10所示，从图中可以看出是等幅振荡。

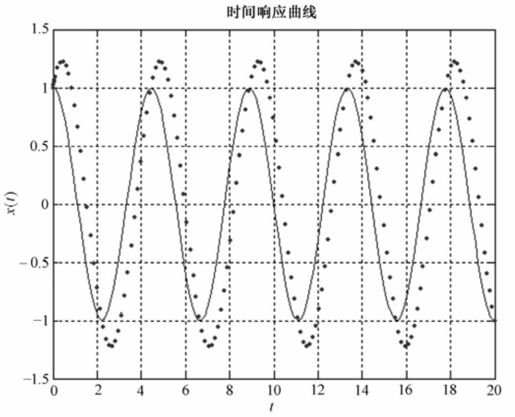
图11.10　例11-2时域响应图

本题的相轨迹是如图11.9所示的椭圆。如果取遍所有的初始值，就会得到无数个一环套一环的椭圆，称为相轨迹场。相轨迹场布满了整个相平面，相轨迹场从全局上展示了动态系统的运动过程，图11.9中只绘出了相轨迹场中的2条相轨迹。

【例11-3】　已知一个二阶非线性系统的微分方程为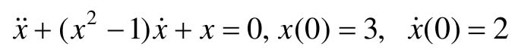：，试用MATLAB函数绘制系统的相平面图。

解：取状态变量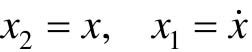，得到系统状态方程模型，即一阶常微分方程组：

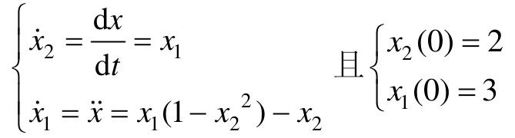
由此模型就可以用MATLAB来求解了。

主程序MATLAB代码如下：

[t, x]=ode45(' test_11_3', [0, 20], [3, 2])       % test_11_3是系统微分方程的描述函数
plot(x(:, 1), x(:, 2))          %绘制相轨迹
axis([-6, 6, -6, 6])          %添加坐标轴的显示范围
xlabel('x');   ylabel('dx/dt')        %添加横纵坐标标注
grid              %添加栅格
title('相轨迹图')       %添加图表题

子函数MATLAB代码如下：

function xdot= test_11_3(t, x)         %状态导数
xdot=[x(1)*(1-x(2)^2)-x(2); x(1)];
%  function xdot=filename(t, x)
%  xdot=[表达式1；表达式2；表达式3;…；表达式n-1]
%  表达式1 对应  x1'=x2; 表达式2 对应  x2'=x3
%  %  表达式3 对应  x3'=x4,…,表达式n-1对应  xn-1'=xn

主函数运行后，输出如图11.11所示。

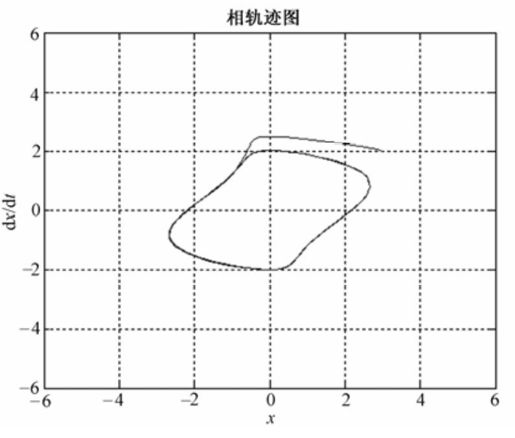
图11.11　例11-3相轨迹图

11.3.2.2　采用Simulink绘制相轨迹图

Simulink对于非线性系统的分析与设计是很有用的，Simulink提供了非线性模块，包括死区、饱和、继电等多种类型的非线性，也能构成很复杂的非线性函数。

下面以实例说明如何在Simulink中使用非线性模块以及如何采用Simulink绘制相轨迹。

【例11-4】　已知一个非线性控制系统如图11.12所示，输入为零初始条件，线性环节为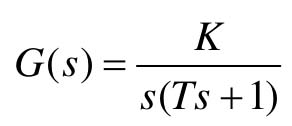，其中，T=1，K=4，N为如图11.2所示的理想饱和非线性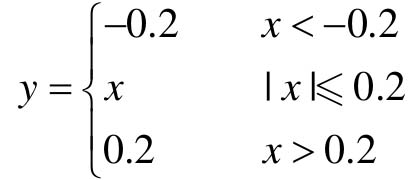，，系统的初始状态为0，试求

（1）在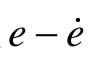平面上画出相轨迹；

（2）绘出e(t)，c(t)的时间响应波形。

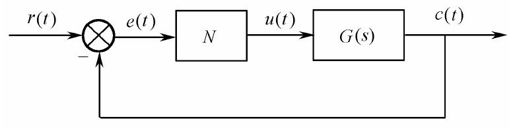
图11.12　非线性控制系统示意图

解：取状态变量，使用Simulink来解此题的步骤如下。

在MATLAB 7.0的MATLAB窗中中双击Simulink图标就打开Simulink Library Browser窗口，再在此窗口进入File\New\Model，打开一个untitled窗（可以用Save as保存此窗口并改名）。

在Simulink Library Browser窗口下有CONTINUOUS、DISCONTINUTIES、MATH OPERATIONS、SINK、SOURCE等子目录，每个子目录下都包含若干可利用的模块，可直接拖至untitled窗口，如图11.13所示。

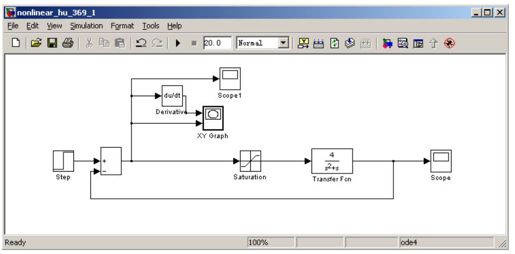
图11.13　例11-4的Simulink仿真模型

在图11.13中，传递函数环节（Transfer Fcn）、微分环节（Derivative）来自Simulink\CONTINUOUS；饱和非线性（Saturation）来自Simulink\DISCONTINUTIES；求和（Sum）来自Simulink\MATH OPERATIONS；双踪示波器（XY Graph）、单踪示波器（Scope）来自Simulink\SINK；阶跃函数（Step）来自Simulink\SOURCE。

要在XY Graph上绘出相轨迹，关键是要得到信号。显然，e直接取自比较器的输出（即图中Sum环节的输出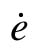），可以在e后面加一微分环节实现，然后把这两个信号接到XY Graph便可画出相轨迹。

双击饱和模块，就会出现该模块的设置窗口，按照题意设置饱和特性的限幅为[-0.2, 0.2]。

在SIMULATION\SIMULATION PARAMETERS\SOLVER中设置SolverType为“Fixed Step”，“Solver”（步长）为0.05，“Stop Time”为40。运行SIMULATION\START，XY Graph绘出的相轨迹如图11.14所示。

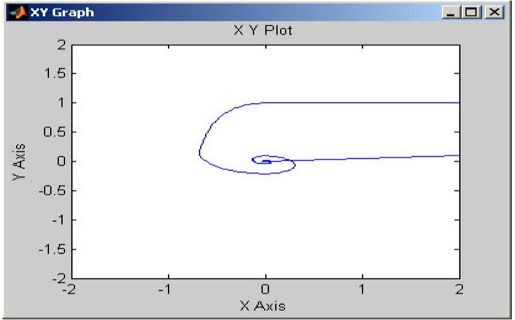
图11.14　例11-4的相轨迹图

双击系统输出连接的单踪示波器，看到c(t)的时间响应波形，如图11.15所示。

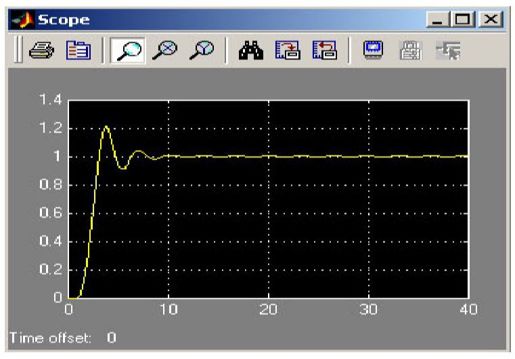
图11.15　例11-4中c(t)的时间响应波形

双击比较环节输出连接的单踪示波器，看到e(t)的时间响应波形，如图11.16所示。

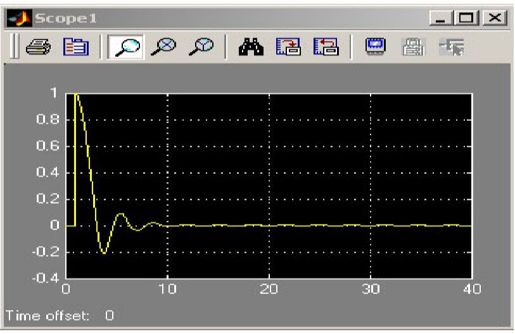
图11.16　例11-4中e(t)的时间响应波形

【例11-5】　已知一个控制系统如图11.17所示，输入为零初始条件，线性环节为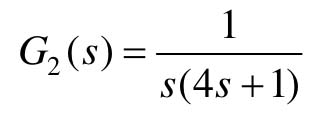，系统的初始状态为0。G1(s)取下列两种情况：

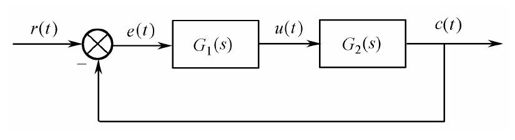
图11.17　例11-5的控制系统框图

（1）G1(s)为非线性环节N，且N为理想饱和非线性，其函数。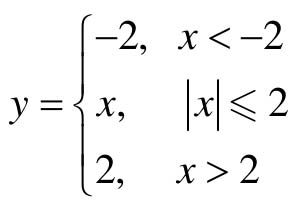

（2）G1(s)为比例环节，比例增益为2。

试求系统在单位阶跃作用下的相轨迹以及系统输出。

解：取状态变量，使用Simulink建立如图11.18所示的仿真框图。

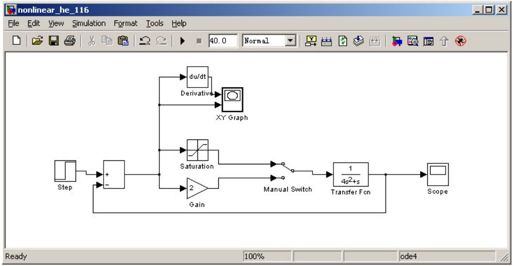
图11.18　例11-5的Simulink仿真模型

在图11.18中，传递函数环节（Transfer Fcn）、微分环节（Derivative）来自Simulink\CONTINUOUS；饱和非线性（Saturation）来自Simulink\DISCONTINUTIES；求和（Sum）来自Simulink\MATH OPERATIONS；双踪示波器（XY Graph）、单踪示波器（Scope）来自Simulink\SINK；阶跃函数（Step）来自Simulink\SOURCE；手动切换开关（Manual Switch）来自Simulink\SIGNAL ROUTING，它用来在同一个图上实现G1(s)两种情况的切换，双击该图标便可实现切换。

要在XY Graph上绘出相轨迹，关键是得到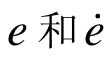信号，显然，e直接取自比较器的输出（即图中的Sum环节的输出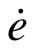），可以在e后面加一个微分环节实现，然后把这两个信号接到XY Graph便可画出相轨迹。

双击饱和模块，就会出现该模块的设置窗口，按照题意设置饱和特性的限幅为[-2, 2]。

在手动开关选择非线性模块后，运行SIMULATION\START，XY Graph绘出的相轨迹如图11.19所示。

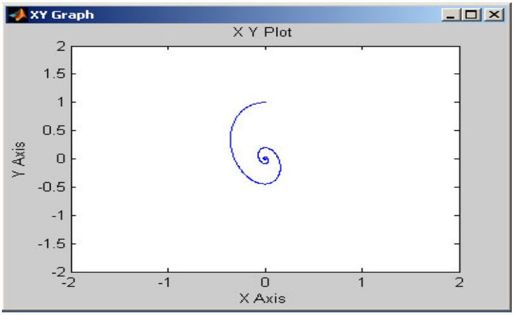
图11.19　G1(s)为非线性环节时的相轨迹图

双击系统输出连接的单踪示波器，看到系统的时间响应波形，如图11.20所示。

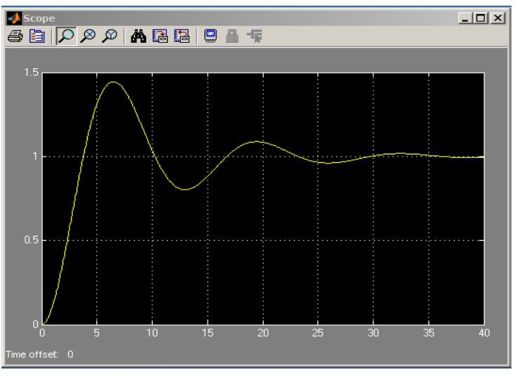
图11.20　G1(s)为非线性环节时的系统输出

在手动开关选择线性模块后，运行SIMULATION\START，XY Graph绘出的相轨迹如图11.21所示。

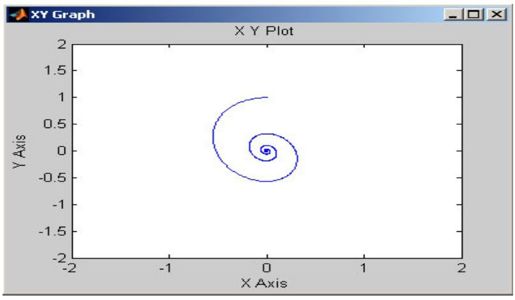
图11.21　G1(s)为线性环节时的相轨迹图

双击系统输出连接的单踪示波器，看到系统的时间响应波形，如图11.22所示。

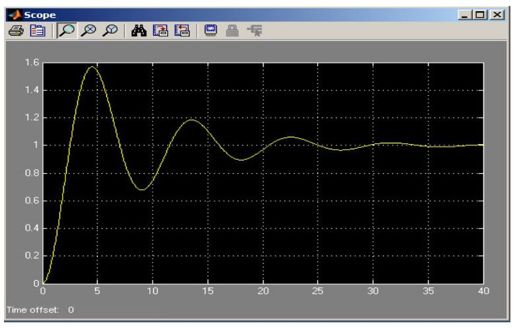
图11.22　G1(s)为线性环节时的系统输出