12.7　综合实例及MATLAB/Simulink应用

下面通过一个综合实例，讲述MATLAB/Simulink在本章中的应用。

【例12-12】　给定单位负反馈离散控制系统，其采样周期为1s，开环传递函数为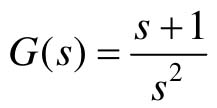H_371-01与零阶保持器ZOH串联；同时，开环增益为K。求闭环系统稳定的条件，并且绘制K取不同值时闭环系统的阶跃响应曲线。

解：使用MATLAB/Simunlink求解本题的基本步骤如下。

【步骤1】　建立系统的数学模型。

首先，建立上述系统的数学模型，MATLAB代码如下：

  1. clc;           % 清除屏幕显示
  2. clear;           % 清除工作空间中的所有变量
  3. % 建立控制系统的数学模型
  4. Ts = 1;           % 采样周期
  5. num = [1 1];           % 传递函数分母多项式系数
  6. den =[1 0 0];          % 传递函数分子多项式系数
  7. sys_continue = tf(num,den)         % 连续系统的传递函数
  8. sys_discrete = c2d(sys_continue,Ts,'zoh')       % 离散系统的传递函数
  9. sys_k = 1;           %系统的开环增益
  10. sys_open = sys_k * sys_discrete           % 系统的开环传递函数

程序运行的结果为：

  1. % 系统的开环传递函数
  2. Transfer function:
  3.   1.5 z - 0.5
  4. -------------
  5. z^2 - 2 z + 1
  6. Sampling time: 1

【步骤2】　绘制系统的根轨迹。

欲确定使闭环系统稳定的K的范围，需要绘制上述离散控制系统的根轨迹图，找出根轨迹和单位圆的交点。程序代码如下：

  1. % 绘制离散控制系统的根轨迹图
  2. figure(1);           % 开启新的绘图窗口
  3. rlocus(sys_discrete);         % 绘制离散控制系统的根轨迹

运行结果如图12.39所示。

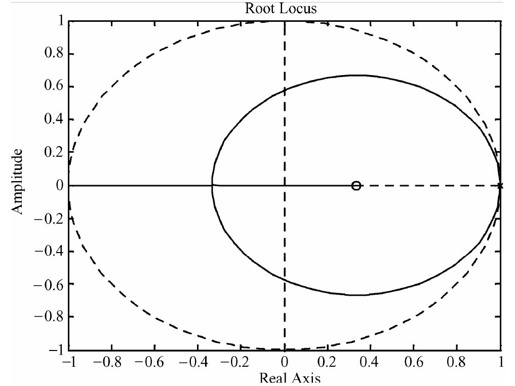
P_372-1

图12.39　离散控制系统的根轨迹图

从图12.39中可以读到交点处的开环增益为K=0，K=2；也就是说，使闭环系统稳定的K的范围是0<K<2。为了验证这一结论，可以绘制系统的幅频特性曲线和Nyquist曲线，观察其稳定性。MATLAB代码如下：

  1. % K = 2 时系统的频率特性曲线
  2. sys_k = 2;           % 设定系统增益为2
  3. figure(2);           % 开启新的图形窗口
  4. margin(sys_k * sys_discrete);        % 绘制离散控制系统的Bode图
  5. % K = 2 时系统的 Nyquist 曲线
  6. figure(3);           % 开启新的图形窗口
  7. [dnum,dden] = tfdata(sys_k * sys_discrete,'v')      % 提取开环传递函数的零极点
  8. dnyquist(dnum, dden, Ts)        % 绘制离散控制系统的Nyquist曲线
  9. grid on;           % 显示网格线

程序运行的结果如图12.40和图12.41所示。

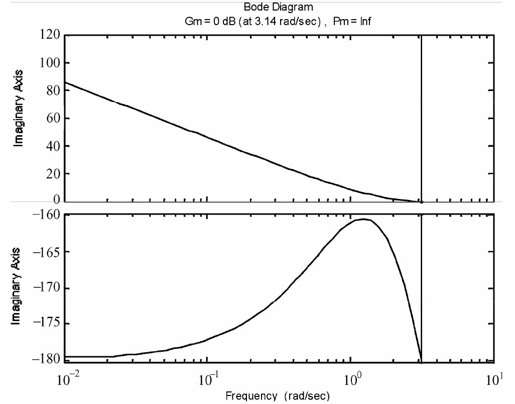
P_373-1

图12.40　离散控制系统的幅频特性曲线

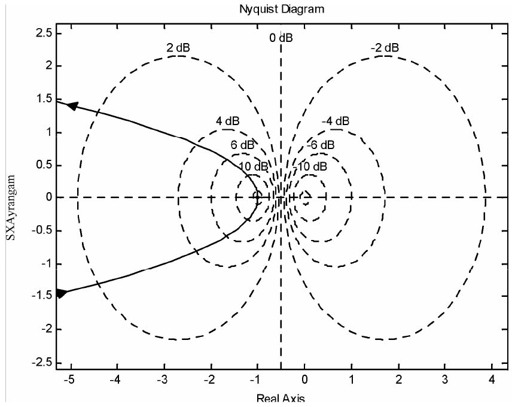
P_373-2

图12.41　离散控制系统的Nyquist曲线

从图中不难看出，当K=2时，系统处于临界稳定状态。幅频特性曲线显示，此时相角裕量为0，增益裕量为0；Nyquist曲线则恰好穿过（-1,0）点。可以确定，系统稳定时K的取值范围为（0, 2）。

【步骤3】　分析系统的阶跃响应。

给K赋不同的值（这里，令K=1、2、3），观察相应的阶跃响应曲线。MATLAB代码如下：

  1. % K 取不同值时系统的阶跃响应曲线
  2. sys_k = 1;           % 设定系统增益为1
  3. figure(4);           % 开启新的图形窗口
  4. sys_close = feedback(sys_k * sys_discrete,1);          % 计算闭环系统的传递函数
  5. [dnumc,ddenc] = tfdata(sys_close,'v');      % 提取闭环传递函数的零极点
  6. dstep(dnumc,ddenc,25);         % 绘制闭环控制系统的阶跃响应曲线
  7. sys_k = 2;           % 设定系统增益为2
  8. figure(5);           % 开启新的图形窗口
  9. sys_close = feedback(sys_k * sys_discrete,1);      % 计算闭环系统的传递函数
  10. [dnumc,ddenc] = tfdata(sys_close,'v');      % 提取闭环传递函数的零极点
  11. dstep(dnumc,ddenc,25);         % 绘制闭环控制系统的阶跃响应曲线
  12. sys_k = 3;           % 设定系统增益为3
  13. figure(6);           % 开启新的图形窗口
  14. sys_close = feedback(sys_k * sys_discrete,1);      % 计算闭环系统的传递函数
  15. [dnumc,ddenc] = tfdata(sys_close,'v');      % 提取闭环传递函数的零极点
  16. dstep(dnumc,ddenc,25);        % 绘制闭环控制系统的阶跃响应曲线

程序运行的结果如图12.42、图12.43和图12.44所示。

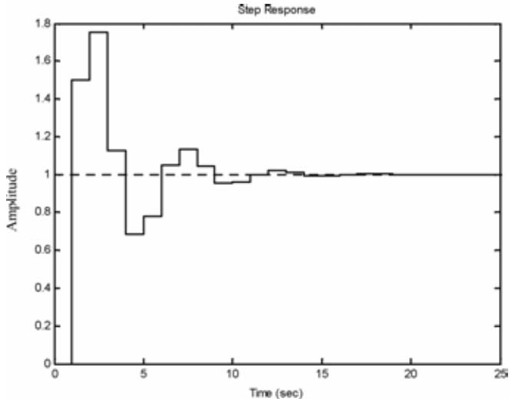
P_374-1

图12.42　K=1时闭环系统的阶跃响应曲线

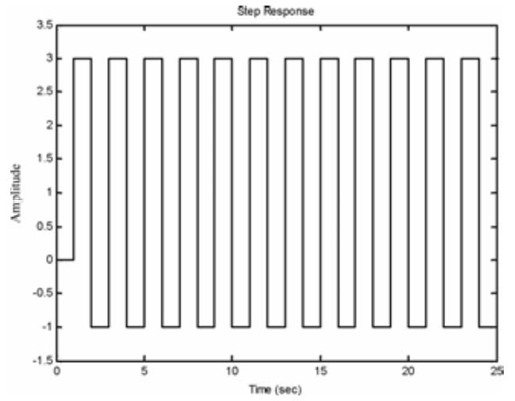
P_374-2

图12.43　K=2时闭环系统的阶跃响应曲线

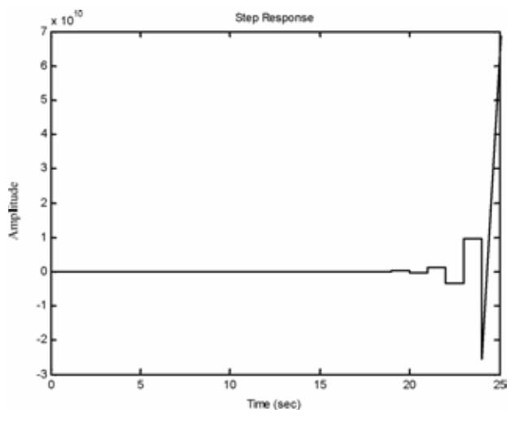
P_374-3

图12.44　K=3时系统的阶跃响应曲线

从以上几幅图中不难看出，当K=1时，闭环系统稳定，阶跃响应曲线收敛，并且系统的静态误差为0；当K=2时，闭环系统临界稳定，阶跃响应曲线等幅振荡；当K=3时，闭环系统不稳定，阶跃响应曲线很快发散。这与上面对K值的讨论结果是完全符合的。

【步骤4】　分析采样周期对系统稳定性的影响。

进一步考察采样周期对系统稳定性的影响。取Ts=0.5和Ts=2，分别计算系统的阶跃响应，代码如下：

  1. % 考察采样周期对系统稳定性的影响
  2. sys_k = 2;           % 设定系统增益为2
  3. figure(7);           % 开启新的图形窗口
  4. Ts = 0.5;           % 设定采样周期为0.5 s
  5. sys_discrete = c2d(sys_continue,Ts,'zoh')       % 计算离散系统的开环传递函数
  6. sys_close = feedback(sys_k * sys_discrete,1);      % 计算离散系统的闭环传递函数
  7. [dnumc,ddenc] = tfdata(sys_close,'v');      % 提取闭环传递函数的零极点
  8. dstep(dnumc,ddenc,25);         % 绘制闭环控制系统的阶跃响应曲线
  9. sys_k = 2;           % 设定系统增益为2
  10. figure(8);           % 开启新的图形窗口
  11. Ts = 2;           % 设定采样周期为2 s
  12. sys_discrete = c2d(sys_continue,Ts,'zoh')       % 计算离散系统的开环传递函数
  13. sys_close = feedback(sys_k * sys_discrete,1);       % 计算离散系统的闭环传递函数
  14. [dnumc,ddenc] = tfdata(sys_close,'v');      % 提取闭环传递函数的零极点
  15. dstep(dnumc,ddenc,25);         % 绘制闭环控制系统的阶跃响应曲线

程序运行结果如图12.45和图12.46所示。

P_375-1

图12.45　Ts=0.5, K=2时系统的阶跃响应曲线

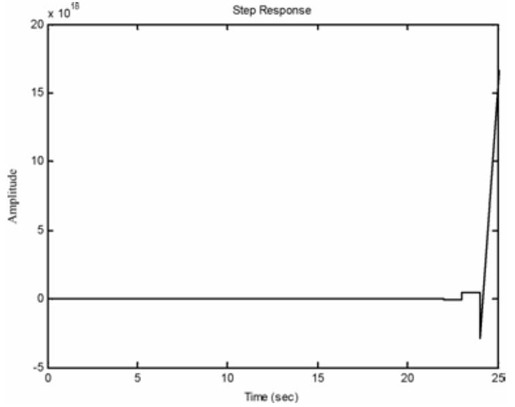
P_375-2

图12.46　Ts=2, K=2时系统的阶跃响应曲线

结果显示，离散控制系统的稳定性不仅与开环增益有关，还与采样周期密切相关。原本临界稳定的系统，在缩短采样周期后变得稳定；加大采样周期则使得系统不稳定。理论计算表明，只有当KT<2时，题设中的离散控制系统才是稳定的。

习　题

【12.1】　给定连续对象的传递函数为

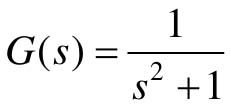
P_376-1

（1）利用MATLAB建立上述控制系统的传递函数模型；

（2）将得到的传递函数模型转化成离散的脉冲传递函数G(z)。

【12.2】　给定离散控制系统的脉冲传递函数为

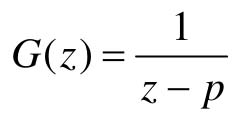
P_376-2

利用MATLAB中的dimpulse命令绘制出以下几种情况下系统的脉冲响应曲线：

（1） p=±1；

（2） p=±0.8；

（3） p=±0.5；

（4） p=±0.3；

（5） p=0。

【12.3】　给定离散控制系统的脉冲传递函数为

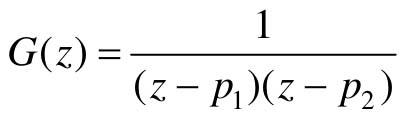
P_376-3

其中，p1, p2是一对共轭极点。利用MATLAB中的impulse命令绘制以下几种情况下系统的脉冲响应曲线：

（1） p1,2=-0.8±0.6i；

（2） p1,2=0.8±0.6i；

（3） p1,2=-0.8；

（4） p1,2=0.8；

（5） p1,2=-0.5±0.866i；

（6） p1,2=0.5±0.866i；

（7） p1,2=0.5±0.4i；

（8） p1,2=0.5±0.4i；

（9） p1,2=±li。

【12.4】　利用MATLAB中的dstep命令绘制第3题几种情况下的阶跃响应曲线。

【12.5】　某离散控制系统结构如图12.A所示。

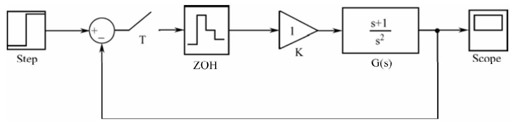
P_376-4

图12.A　习题

（1）利用MATLAB建立上述控制系统的模型；

（2）分别取不同的增益值K和周期值T，绘制系统的阶跃响应曲线，分析系统的稳定性；

（3）比较各条曲线之间的异同，并从中得出结论。

【12.6】　给定离散控制系统的结构如图12.B所示。

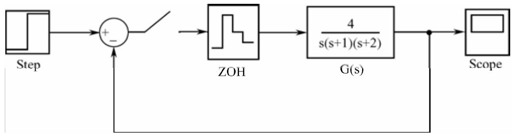
P_377-1

图12.B　习题

（1）利用MATLAB建立上述控制系统的模型；

（2）采样周期为1 s，判断系统的稳定性，并绘制系统的阶跃响应曲线。