2.1 随机变量及其分布
2.1.1 随机变量的概念
在同一组条件下,对某事物或现象所进行的观察或实验叫随机试验(experiment),把观察或实验的结果叫随机事件(event)。例如,抛掷一枚质地均匀的骰子就是一次试验,骰子落地,可能出现1点,2点,…,6点,或为奇数点或为偶数点,点数大于5,等等,这些就是一个个事件。这些事件在一次试验中可能出现也可能不出现,我们称之为随机事件。
如果随机试验的每种结果可以用一个数字作为其代表,则我们称此变量为随机变量(randomvariable)。例如掷骰子试验中,骰子落地,将可能出现的点数作为考察的变量X,则X就是一个随机变量。此随机变量可以取的值仅限于1~6这六个正整数。在此范围内,随机变量究竟在一次试验中会出现哪一个值,在试验前是完全不能确定的。通常的随机变量都具有这种性质和特点,即事先可以肯定取值的范围,但不能肯定具体的取值是多少。同样,在掷两颗骰子试验中,我们可以定义所掷两颗骰子“点数和”为一个随机变量Y,它的取值范围就是2~12的这些整数,投掷之前不知道此随机变量取值是几。当然,你也可以定义所掷两颗骰子“点数差(绝对值)”作为另一个随机变量Z,那么它的取值范围就将是0~5这六种结果。
概率论并不能确定一次试验下随机变量所取的值是多少,它所要研究的是随机变量所取之值的规律,即出现各种结果的可能性如何。例如,在掷骰子试验中,随机变量取1~6这六个整数的可能性全都相同,都是1/6。掷两颗骰子点数和的这个随机变量,取值范围是2~12的这些整数,但取这些值的可能性很不同,取值为7的可能远大于取值为2的可能。描述出现各种结果的可能性规律的就是分布律。
随机变量的取值有两种不同的类型。
第一种是离散型(discrete)随机变量。例如,检查一个产品是否合格,可能有“合格”及“不合格”两种结果,可以分别用0,1代表。例如,市场手机有A,B,C共三种,这里没有顺序可言,但可以分别以1,2,3代表。又如,车间产品分一等品、二等品及三等品;满意性分为“极不满”、“不满”、“尚可”、“满意”、“极满意”五等,这些是有顺序可言的。同样可以分别规定产品等级为1~3共三种,对于满意度可以规定为1~5共五类,等等。
另一种是连续型(continuous)随机变量。例如,自动车床生产的螺钉直径、长度,每台手机的发射功率,等等。这些随机变量的取值通常是某个实数区间,此区间可以是有限的,也可以是无限的。连续型随机变量的应用要比离散型随机变量广泛得多。
随机变量的两种数据类型不同,处理方法也不同。我们再看些例子。设X为某铸件上的缺陷点数,X可以取0,1,2,…可能值。因此,X是离散型随机变量。类似地,手机外壳透明显示框内包含的气泡数、布匹上的疵点数、车床一天内发生的故障次数、京津高速公路上的事故数等,都是取值为{0,1,2,3,…}的离散型随机变量。射击飞碟比赛,共发10枪,命中飞碟的次数也是离散型随机变量,其取值域为{0,1,2,…,10}。
再比如,设X为某品牌手机电池的寿命(单位:小时),则X是在[0,∞)上取值的连续型随机变量。类似地,PCB板上焊锡膏涂层厚度、硝酸铵化肥反应罐每天的产量等,都是在[0,∞)上取值的连续型随机变量。
2.1.2 随机变量分布的概念
随机变量通常用大写字母X,Y,Z等表示,随机变量的取值常用小写字母x,y,z等表示。我们已经知道,随机变量可以分为两类:连续型随机变量和离散型随机变量。
为了描述随机变量的分布规律,我们对这两种类型分别讲述。
2.1.2.1 离散型随机变量的分布律
对于离散型随机变量,我们可以将其所有可能的取值排列起来。例如,掷骰子试验中,将可能出现的点数这个随机变量记为X,则这就是一个离散型随机变量。此随机变量可以取的值xi是1~6这六个整数。由于取这六个数的概率全相等,都是1/6,因此分布律可以写成下列形式(见表2—1):
表2—1 掷1颗骰子点数分布律表

在掷2颗骰子的试验中,将可能出现的点数和这个随机变量记为Y,则此离散型随机变量可以取的值yi是2~12这11个整数。由于取这11个数的概率不全相等,因此要把取每个不同值的概率分别写出,因此分布律可以写成下列形式(见表2—2):
表2—2 掷2颗骰子“点数和”Y的分布律表

一般说来,我们可以先将离散随机变量所有可能的取值,沿水平方向排成一行,在每个值的下方列出随机变量取此值的可能性,这个表就称为离散型随机变量的分布律。当然,这里所有列出的概率一定是非负数,而且所有这些概率之和应恰好为1。
我们再看几个离散型随机变量分布律的例子。
例2—1
在M电子公司生产的简易二极管中,按质量等级可分为5级,其中1级最差,5级最好。现统计了今年1月份生产的二极管质量各种等级所占比率(见表2—3)。
表2—3 质量等级分布状况表

为了直观显示概率分布的状况,我们可以画出分布律图。在研究二极管质量等级分布状况的例子中,记X为任意抽取一个二极管的质量等级数,则X是个以表2—3为分布律的离散型随机变量。图2—1就是二极管质量等级的概率分布律图。
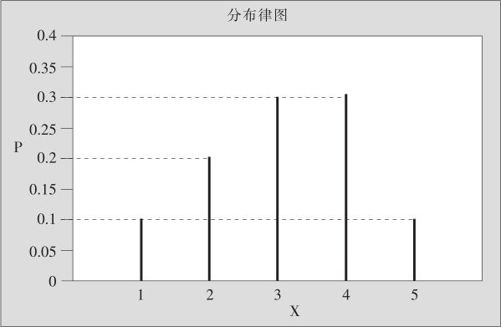
图2—1 质量等级分布律图
由于画出概率分布律图非常重要,在很多计算机软件中,都可以直接画出离散随机变量的分布律图来。例如,用MINITAB软件,先形成一个离散分布律的数据表,如图2—2所示。

图2—2 离散分布律输入数据表
在图2—3中介绍了画图的具体过程:从“图形>概率分布图(Graph>Distribution)”进入,选“单一视图(Simple)”,然后在各种分布中选“离散(Discrete)”,指定“值在(value)”为“等级”,指定“概率在(probability)”为“P”,则计算机可以直接画出如图2—4所示形状的分布图。
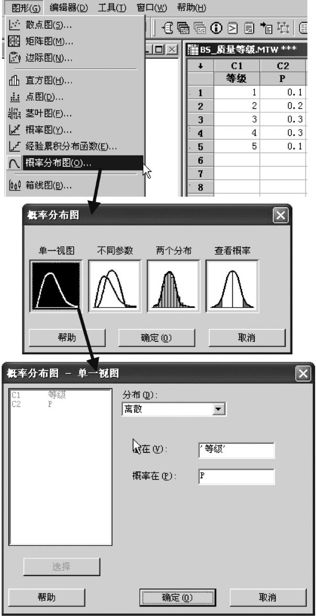
图2—3 画离散概率分布律图的MINITAB操作流程
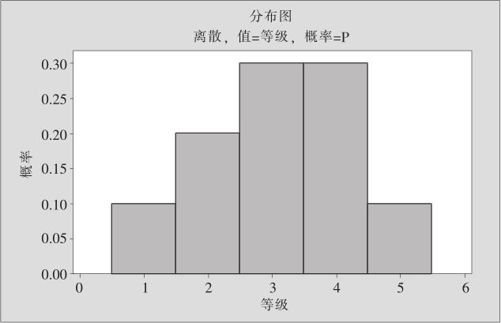
图2—4 质量等级分布律图
还有另一种方法可以画离散型的分布律图。
如图2—5所示。从“图形>散点图(Graph>Scatterplot)”窗口进入,选“简单(Simple)”,出现如图2—5所示的界面。再以“P”为纵坐标,以“等级”为横坐标,则可以画出散点图,再在“数据视图(Data View)”选项中在原来已有的“符号(symbols)”的基础上,加选“投影线(Project Line)”项,则可以画出在每个点的下方带投影线的图(见图2—6)。
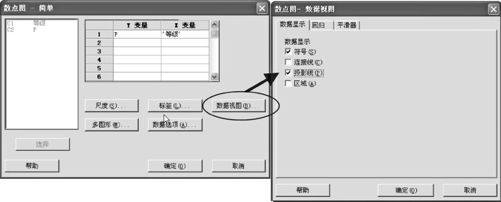
图2—5 画柱状图的MINITAB操作流程
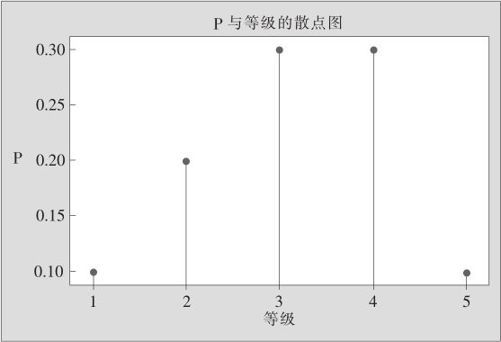
图2—6 质量等级分布律图(柱状图)
2.1.2.2 连续型随机变量的分布
我们平时都有直方图的概念,对它的详细介绍将在第3章给出。例如,对收集到的1213名成年男子身高数据绘制出频数直方图,如图2—7所示。频数直方图可以清楚地显示出在不同取值处,取值可能性的大小状况,身高在162cm~174cm的人比别的身高人数要多很多。但要注意,这里画的只是频数直方图。直方图的纵坐标可能是频数,也可能是频率,观测值的个数发生变化,或区间的划分方法发生变化时,纵坐标就会发生变化。我们可以这样设想,当数据个数很多、组距很小、组数很多时,连接直方图中每个矩形上边中点的折线就接近一条光滑的曲线了,图2—7给出了这样的描述。
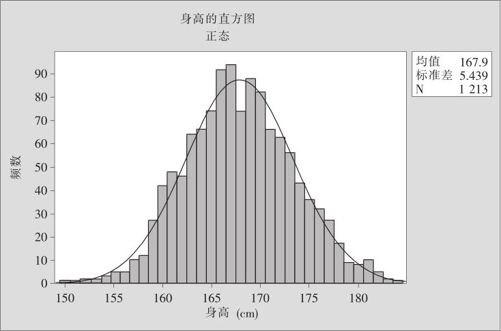
图2—7 中国成年男子身高抽样分布图
随着数据的不断增加,频率趋于稳定,频率的稳定值就是概率。如果要求整个曲线下方的面积恰好为1,则这条曲线就称为概率密度曲线,此密度函数就是概率密度函数(probability density function,pdf),如图2—8所示。
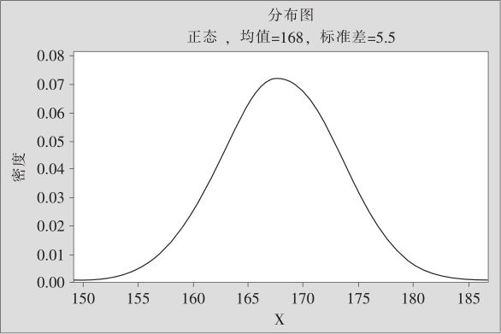
图2—8 中国成年男子身高(单位:cm)概率密度分布图
请注意比较一下,在图2—7与图2—8中,两条曲线形状完全相同,但二者的纵坐标是不相同的。图2—7中,纵坐标高度与观测值总个数及身高间隔的划分都有关系,但图2—8则不然,光滑曲线下方的面积固定为1,它的曲线高度与抽样人数及间隔的划分都无关。可是,对于概率密度曲线而言,它仍然与选用单位有关。例如,在图2—8中,身高的单位是厘米,其密度的最大值大约是0.07,如果我们把身高的单位换成米(厘米的100倍),则其密度的最大值也要扩大100倍,大约是7,如图2—9所示。也就是说,密度是有量纲的,它的量纲是1/[X]。
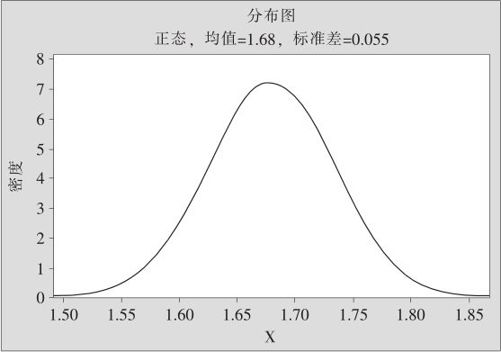
图2—9 中国成年男子身高(单位:m)概率密度分布图
概率密度函数是描述连续随机变量分布的最重要和最基本的工具。概率密度函数应该有什么特点呢?如果p(x)是连续随机变量X的概率密度函数,则p(x)应该满足下列条件:
p(x)≥0,概率密度函数肯定为非负数。

这就是说,概率密度函数曲线与横轴所围成的面积永远为1。

这就是说,随机变量落入[a,b]的概率就等于密度函数曲线在[a,b]上的积分。其含义如图2—10所示。
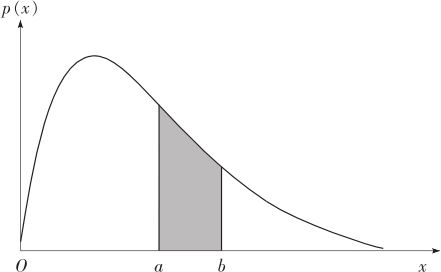
图2—10 事件的概率与概率密度分布的关系图
这样一来,就看到概率密度函数的重要性。因为如果我们得到了概率密度函数,就可以直接求出随机变量落在任意一个范围内的概率。这一点在今后的统计计算中起了关键的作用。
