7.3　单样本Wilcoxon符号秩检验法

对于单样本的中位数检验方法，我们曾在7.1节介绍了符号检验法，并讨论了例5—3面粉重量的检验问题。但符号检验法粗糙，检验功效很低。统计学家Wilcoxon研究出了一种精密得多的“符号秩检验法”。我们先用一个数字例题说明这种方法的原理，然后再次讨论例5—3，并获得了显著性检验结果。

例7—8

我们收集到了12个数据，如表7—6所示（数据文件：NP_符号秩.MTW）。

表7—6

试问，能认为这批数据的中位数是24吗？取α＝0.05。

解　我们要检验的问题是：

H₀：η＝24

H₁：η≠24

我们把数据按从小到大的顺序排好（见表7—7中第1行）。

表7—7　单样本Wilcoxon符号秩检验表

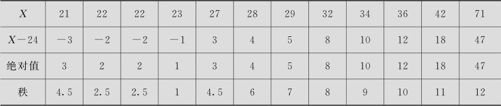
如果单看符号，12个数据中，数值小于24的有4个，数值大于24的有8个，用计算机或查附表8都无法拒绝原假设。但我们看到，小于中位数的观测值个数虽然高达4个，但它们都与24很接近，相差并不多；反之，大于中位数的观测值不仅个数多，而且比设定中位数高了很多。我们将求出观测值与设定中位数之差（列在表7—7中第2行），再取绝对值（见表7—7中第3行），再对绝对值求秩（见表7—7中第4行）。

这里按正负号分了两组，样本数分别为4及8，对两组分别求秩和，其中负号组的秩和为W^-＝4.5＋2.5＋2.5＋1＝10.5。查附表9，对应于n₁＝4，n₂＝8，在左栏查得接受域为（14，38），T值比下界14还小，落入接受域之外了，因此应拒绝原假设，即不能认为此组数据的中位数为24。

MINITAB软件的操作如下。依次选择“统计＞非参数＞单样本Wilcoxon（STAT＞Nonparametric＞I-Sample Wilcoxon.）”（见图7—7），填写变量名即可得到结果。

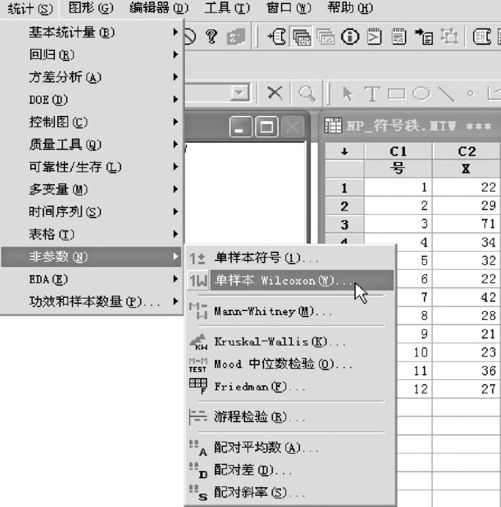
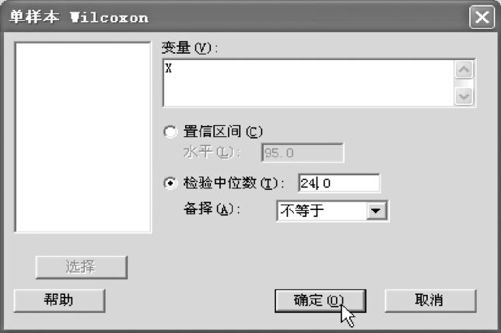
图7—7　单样本符号秩检验操作图

Wilcoxon符号秩检验：X

中位数＝24.00与中位数≠24.00的检验

例7—9（续例5—3）

抽查精细面粉的装包重量，抽查了16包，其观测值如表7—8所示（数据文件：BS_面粉重量.MTW）。

表7—8

试检验平均重量与原来设定的20kg是否有显著差别。取α＝0.05。

解　此问题是要检验：

H₀：m＝20

H₁：m≠20

本例在例7—5中按符号检验法讨论过，当时由于数据中比20小的有6个，比20大的有10个，因而检验结果是不能拒绝原假设，无法断言平均值与此20有显著差别。表7—9中记述了符号秩检验法，在对于与20的差值（第2行）取绝对值（第3行）后，计算了各自的秩（第4行）。这里按正负号分了两组，样本数分别为6及10，对两组分别求秩和，其中负号组的秩和为：

W^-＝5.5＋10.5＋1.5＋1.5＋3.0＋4.0＝26

表7—9　面粉重量数据的符号秩检验

正号组的秩和为：

W⁺＝15.0＋12.0＋8.0＋9.0＋13.5＋13.5＋10.5＋5.5＋16.0＋7.0＝110

由于W^-＋W⁺＝1＋2＋…＋16＝136，因此W⁺不用再次求和，而可以用下式算出：

W⁺＝136－W^-＝136－26＝110

查附表9，对应于n₁＝6，n₂＝10，在左栏查得接受域为（33，69），T值26比下界33还小，落在接受域之外了，因此应拒绝原假设，即不能认为此组面粉数据的中位数为20。

使用MINITAB软件计算，操作方法与例7—8完全相同，可以得到下列结果：

Wilcoxon符号秩检验：面粉重量

中位数＝20.00与中位数≠20.00的检验

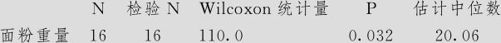
由于p值＝0.032＜0.05，因此应拒绝原假设，即不能认为此组面粉数据的中位数为20。与在例7—5中按符号检验的结果相比，可以看出符号秩的检验法比简单的符号检验要灵敏得多。但是，这里也要明确使用符号秩检验法所需要的条件：一是样本要来自连续随机变量总体（符号检验并不需要此条件）；二是要求总体分布的对称性较好。当总体对称性较差时，则还是符号检验更可靠。对于在本例中所使用的面粉重量的数据，可以看出其对称性是很好的，使用符号秩检验的结果是可信的。