9.4　离散变量Logistic回归

前面几节讨论了一元及多元线性回归的问题，其中因变量一定是连续型随机变量。在有些实际问题中，响应变量可能是离散型的，而自变量依然是连续型的，例如，每个人的体重指数（body weight index，BWI）定义为BWI＝体重（公斤）／身高（米）²，这是连续变量，希望讨论是否随BWI的增加患心血管疾病的比率也会增加？这时，响应变量取值只有“患有”或“未患有”两类，我们把这类只取两值的响应变量对于单个或多个自变量的回归问题称作离散变量的回归分析。回归分析的模型对于比率要用到Logistic变换，所以称这种回归为离散变量的Logistic回归。更一般地，离散随机变量还可以取多个离散值，其中一种是“名义变量”，例如3种品牌、4门课程等；还有一种是“有序变量”，空气污染指数分4级，从1级到4级是有顺序可言的；这两种类型问题也都可以借助于二值Logistic回归而得到解决。在本部分中，首先在9.4.1节讨论二值Logistic回归，在9.4.2节讨论一般名义值的Logistic回归，最后在9.4.3节讨论有序样本的Logistic回归问题。

9.4.1　二值Logistic回归

本节只讨论响应变量取值只有“是”或“否”两类，我们把这类只取两值的响应变量对于单个或多个自变量的回归问题称作二值Logistic回归分析（MINITAB称之为“二进制Logistic回归分析”）。

例9—7

研究肥胖是否与患心血管疾病有关的问题。上海某高校对于3983名参加体检者，记录了体重超重者（BWI大于等于25）患有心血管疾病的人数。其数据列于表9—9（数据文件是：REG_心血管疾病.MTW）。希望分析体重指数（BWI）与心血管疾病患病率的关系。

表9—9　体重指数与患心血管疾病数据表

解　从上表最后一行看出，患病率有随BWI增加而增长的趋势，但这是否为规律性的结果？更具体地，对于给定的BWI，估计其患心血管病率为多少？因此要对这种数据进行回归分析。显然，用患病率p直接作为因变量y效果肯定不好，因为p的变化范围是从0到1，拟合线性回归肯定不行，要对p进行变换才好。

定义两种结果出现的概率之比为“优势比”或“差异比”（odds ratio），其定义是：

当事件发生概率从0变化到1时，优势比从0变化到正无穷。当事件出现概率从不可能（p＝0）慢慢增长时，优势比逐渐增大；当事件出现概率恰好为1/2时，优势比为1，即“出现”或“不出现”的可能性相等；一旦事件出现概率大于1/2时，优势比将大于1，即“出现”比“不出现”的可能性大很多；p值越来越大时，优势比也越来越大，这表示“出现”比“不出现”的可能性大得越多，直到p→1时而优势比趋于无穷。

求优势比的对数，则发现优势比的对数将从负无穷变化到正无穷。故定义：

希望建立y与一个x或若干个连续自变量x₁，x₂，…，x_k的线性回归：

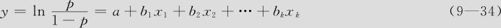
反解式（9—34），可得

特别对于只有一个自变量时，方程（9—35）可以变成：

称式（9—36）为Logistic函数。当x从负无穷变到正无穷，y也从负无穷变到正无穷，即它们取整个实数轴时，p从0变到1。用这种类型的函数来拟合比率的变化规律是再好不过的了。所以，Logistic变换式（9—33）对于二值回归起着关键的作用。

打开数据文件时，请注意数据的存放格式（见表9—10）。

表9—10　心血管疾病与肥胖数据表

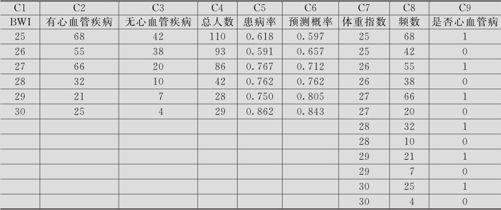
数据存放格式可以有两种方式。一种是从C1到C3这3列是按“事件／试验”格式记录的，新增加的C4列是必需的，它是通过计算而获得的“总人数”；另一种是从C7到C9这3列，是按“响应／频率”格式记录的，其中响应列C9是响应变量，对于“有心血管疾病”用“1”记录，“无心血管疾病”用“0”记录。一般认为用“事件／试验”格式记录更方便简洁。

选择指令“统计＞回归＞二进制Logistic回归（Stat＞Regression＞Binary Logistic Regression）”，得到的界面见图9—33中左半部分。填写信息：选定“事件／试验格式的响应”，在“事件数”中填写“有心血管疾病”；“试验数”填写“总人数”；“模型”填写“BWI”；选“存储”窗，打开后，存储“事件概率”。本例当然也可以在填写信息时选用“响应／频率格式的响应”，结果完全相同。

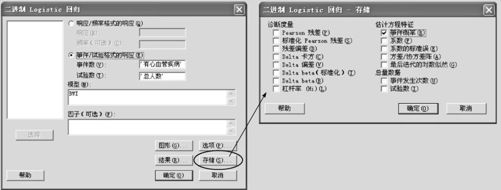
图9—33　二进制Logistic回归操作图

计算后可得如下结果：

二进制Logistic回归：有心血管疾病，总人数与BWI

Logistic回归表

对数似然＝-235.051

检验所有斜率是否为零：G＝11.465，DF＝1，P值＝0.001

对于此表的解释是：

1．在Logistic回归表项下，首先给出了回归方程：

在“检验所有斜率是否为零”一行中，得知G统计量的值为：G＝11.465，自由度DF＝1，p值＝0.001。说明整个模型效果是显著的。这一段的作用与连续变量回归中的ANOVA作用相同，判断的是回归总效果。在各自变量效应的检验中，其系数为0.257，这代表，体重指数每增加一级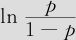，将增加0.257，也即优势比（患心血管病比率与未患心血管病比率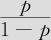）将增加e^0.257＝1.293倍。

2．从拟合效果来看，3种拟合检验方法的p值（H₀：拟合无显著差异；H₁：拟合有显著差异）都大于0.05，故可以认为拟合是满意的。具体的拟合情况中列出了5个组（BWI从25到28，最后BWI＝29与BWI＝30两组由于观测值有的格小于6，故予以合并），对“有心血管病”和“无心血管病”两种情况分别计算了预期频数和实测频数的结果，可以看出二者是很接近的。

拟合优度检验

观测和期望频率表：

（有关Pearson卡方统计量，请参阅Hosmer-Lemeshow检验）

从计算机输出“存储”结果中，可以找到对于相应BWI值的预测概率，并将输出的结果整理成下列表格（见表9—11）。

表9—11　实际与预测患有心血管疾病比较表

对于上述表格，如果把BWI作为横坐标，分别以实际患有心血管病比率与预测概率为纵坐标，可以画出患病率与BWI的关系图（见图9—34）。例如，我们可以预报，BWI达到29的人，患有心血管病的概率高达80.5％。

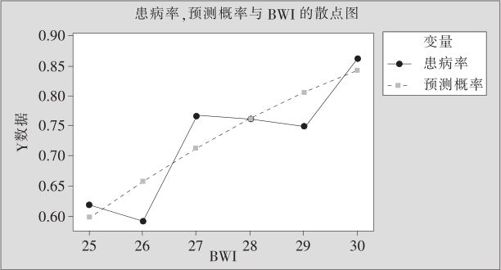
图9—34　心血管病的实测患病率与预测概率对照图

3．相关性度量结果：

相关性度量：

（响应变量与预测概率之间）

找到了规律性的结果离能够准确预报还差很远。这样以BWI来预报患有心血管病究竟预测效果如何？看看预报的实际结果。我们在数据中共收集了267个“患有心血管病”者，121个“未患心血管病”者，所有可能搭配的“配对”共有：267×121＝32307个。在这些配对中，我们逐一检查，是否都是“BWI大则容易患心血管病”。符合这一规律者，一共有16025对，占总观测值的49.6％；不符合这一规律者，一共有9449对，占总观测值的29.2％；BWI值持平者（称为“结”）一共有6833对，占总观测值的21.2％。这些结果可以评价预报效果（即与实际结果的一致性）之好坏。Somer D，Goodman-Kruskal Gamma及Kendall Tau-a都是一致性结果的度量，三者的分子都是“一致对”的数量减去“不一致对”的数量（本例是16025－9449＝6576），分母则三者不同：Somer D以“总对数”为分母（本例是32307）；Goodman-Kruskal Gamma是以扣除“结”的“总对数”为分母（本例是32307－6833＝25474）；Kendall Tau-a是以“所有可能的观测值对数”（本例是387×388/2＝75078）为分母，计算出的这三个统计量值分别为0.20，0.26，0.09，都还嫌太小了些。实际上，单凭“BWI是否大”就断言“是否发作过心血管病”还是很不充分的，预测出错的可能性还是较大的。

本例题比较简单，连续型的自变量只有一个，如果有其他的连续型自变量，可以照样列在“模型”一格中（参见图9—33中左半部分）；如果影响响应变量的还有其他离散型自变量，则可以把它们同时填写在“模型”和“因子”两个窗内。下面举一个例子，这里自变量内含一个连续型自变量和一个离散变量。

例9—8

我国在1990年进行了第四次全国人口普查，将婚姻状况分为“有配偶”、“丧偶”、“离婚”和“未婚”四类。在过去的一年中，按年龄和婚姻状况分别统计了总数及死亡人数，其数据列在表9—12中（摘自王静龙、梁小筠编著：《定性数据分析》，137页，上海，华东师范大学出版社，2005）（数据文件：REG_上海人口死亡率.MTW）。希望分析不同婚姻状况下的死亡率与年龄间的关系，并判断死亡率是否与年龄和婚姻状况有密切关系，判断哪种婚姻状况死亡率最低。部分数据存储格式见表9—13。

表9—12　各年龄组和各类婚姻状况的居民人数表

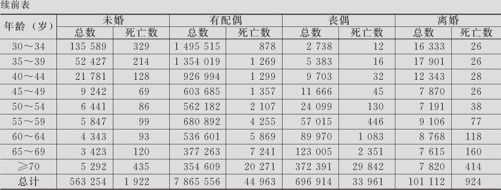
表9—13　上海各年龄组和各类婚姻状况的居民人数表存储格式（部分）

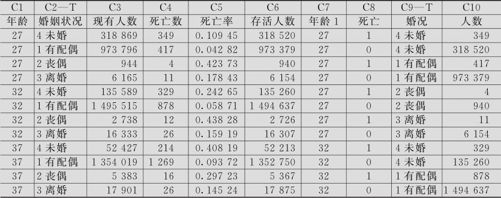
此例题性质与例9—7完全相同，只是这里增加了一个属性自变量。数据存放格式同样可以有两种方式：从C1到C4这4列是按“事件／试验”格式记录的；从C7到C10这4列是按“响应／频率”格式记录的。操作也大体与例9—7相同：选择指令“统计＞回归＞二进制Logistic回归（Stat＞Regression＞Binary Logistic Regression）”，得到的界面见图9—33中左半部分。填写信息：“事件数”填写“死亡数”；“试验数”填写“现有人数”；“模型”填写“年龄婚姻状况”，“因子”填写“婚姻状况”；选“存储”窗，打开后，存储“事件概率”。结果如下：

Logistic回归表

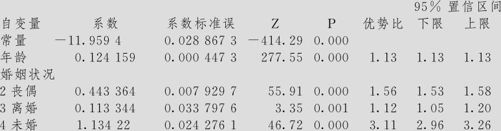
对数似然＝-370473.217

检验所有斜率是否为零：G＝194750.423，DF＝4，P值＝0.000

在Logistic回归表项下，首先给出了4个回归方程：

我们对于婚姻状况取“有配偶”作为“参考选项”，“有配偶”项的截距系数为-11.9594是计算结果直接给出的，其余婚姻状况的截距系数都要自行补算。例如，“丧偶”项的截距系数应为-11.9594＋0.443364＝-11.5160，其余类推。在“检验所有斜率是否为零”的一行中，得知G统计量的值为：G＝194750，自由度DF＝4，p值＝0.000。说明整个模型效果是显著的。这一段的作用与连续变量回归中的ANOVA作用相同，判断的是回归总效果。在各自变量效应的检验中，年龄的p值＝0.000，效应显著，说明年龄的不同导致死亡率显著不同（这是大家都知道的常识）；不同婚姻状况的p值也都为0.000（离婚的p值为0.001），说明各种婚姻状况的死亡率与“有配偶”这个“参考选项”之寿命状况的不同也是显著的。

在式（9—38）中可以看出，各种婚姻状况的年龄变量之回归系数是相同的0.124，这代表，年龄每增加1岁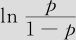，将增加0.124；年龄每增加5岁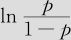，将增加0.620，也即优势比（死亡率与存活率的比值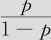）将增加e^0.620＝1.859倍。

计算结果中的死亡概率是小数格式，将数值乘以100，并稍加整理，可以得到百分数死亡概率表（见表9—14中C22～C25）：

表9—14　上海各年龄组和各类婚姻状况的死亡概率预报表

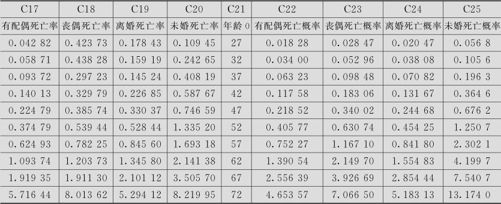
与原来直接计算的实际死亡率（见C17～C20）相比，拟合结果并不太好，但大体趋势及总的规律还是一致的。将表9—14数据C21～C25画出图来（见图9—35），可以看出各种死亡概率预报的变化趋势。这里，有配偶的死亡概率最低；离婚、丧偶次之；未婚者死亡概率最高。这与社会科学的一般原理是吻合的。

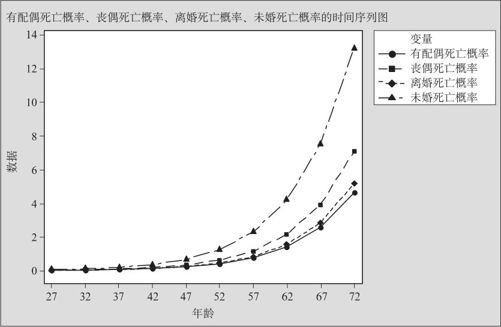
图9—35　上海各类婚姻状况的死亡概率预报结果图

值得注意的是，如果不考虑年龄，将表9—12中最后一行数字取出，笼统比较4种婚姻状况的死亡率，利用列联表的卡方检验，将得出结论：4种婚姻状况的死亡率间确有显著差异，未婚者死亡率最低，有配偶、离婚者次之，丧偶者死亡率最高（总和数据列在“REG_上海人口死亡率.MTW”的C12～C14内）。而“未婚者死亡率最低”这个结论当然是错误的。比较不同婚姻状况的死亡率时，不同年龄段的人口数据是不能直接求和的，这是因为未婚者绝大多数处于死亡率很低的年青阶段，求总和将极大地掩盖未婚者内中老年后死亡率很高这样的事实。不同婚姻状况死亡率的比较应该以比较细致的Logistic回归分析结果为准。

这里引申出一个很重要的观点。六西格玛管理中强调“一切结论要从数据的统计分析出发”，而统计分析时必须注意统计方法的准确性、适用性。例如这里举的人口死亡率的例子，使用简单的列联表卡方检验方法可以得出“未婚者死亡率最低”这个结论，而且在统计检验时差异是高度显著的，但这个结论并不正确。因为列联表卡方检验这种方法是较粗糙的，它没有考虑年龄这个重要因素，因而可能导致得到错误结论，这是在使用统计分析方法时必须注意到的。

9.4.2　名义值的Logistic回归

在9.4.1节讨论了响应变量取值只有“是”或“否”两类的二进制Logistic回归分析。实际工作中，我们还会见到响应变量取名义值的情形，这个响应变量可以取多个值，但这些值又不存在顺序关系。例如响应变量是手机品牌，它有A，B，C，D共4种，4种品牌间不存在顺序关系；又如响应变量是某车间的“车床”、某工厂的“工人”、生产某产品的“方法”等，这些响应变量都是名义值。当响应变量是名义值类别变量（即离散变量），自变量中有数值变量和类别变量，求出这些量之间的关系之数学模型就是名义值Logistic回归问题。常用的名义值Logistic回归数学模型是：从响应变量取的值中选一个为参考事件，例如选取最后一个，即第k个事件，设响应变量取它的概率为p_k，响应变量取其余事件概率为p₁，…，p_k－1；名义值Logistic回归方程模型为：

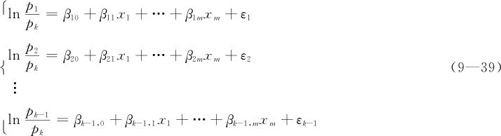
式中，β₁₀，…，β_1m，β₂₀，…，β_2m，…，β_k－1，0，…，β_k－1，m是未知参数；x₁，…，x_m是自变量；ε₁，…，ε_k－1是误差。具体估计未知参数的方法很复杂，用MINITAB的“名义Logistic回归”对话框可以完成有关计算，我们不必过问求解的具体细节。当估计出参数β₁₀，…，β_1m，β₂₀，…，β_2m，…，β_k－1，0，…，β_k－1，m后，就得到回归方程组

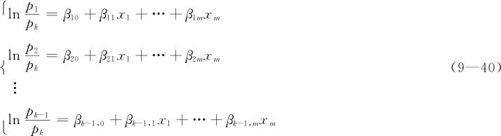
注意这里各行的分子与分母之和并不到1，这是名义Logistic回归与二值Logistic回归不同之处。同样，这里也省略了式（9—40）中估计量上的“^”符号，因为用观测值所得到的概率值只能是真正概率值的估计值，为了书写简单而略去了。另外，这里计算要稍复杂些，先要对于给定的自变量x₁，…，x_m预测出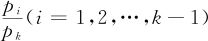，再由p₁＋…＋p_k＝1才能得到p₁，…，p_k的预测值。

在进行名义Logistic回归计算之前，先要把因变量的某个值选定作为参考事件。在操作MINITAB时，先进入“名义Logistic回归—选项”对话框，在参考事件空格中输入选定的参考事件名称，注意：该名称要夹在两个西文半角的双引号之间。如果你不指定参考事件，MINITAB自动按照字典序指定最后的一个事件为参考事件，如果各事件以中文表示，则以汉语拼音的英文字符顺序最后一个事件为参考事件。

由式（9—40）预测各事件的概率的计算比较麻烦。如果预测所用自变量的值已经出现在原始数据中，则可以像例9—7那样用MINITAB计算各事件的概率。具体实施方法是：进入“名义Logistic回归—存储”对话框后，在“输入事件数”空格中填写因变量的事件总个数，勾选“事件概率”，点击“确定”，则MINITAB在工作表中给出各次观测值各事件概率，详见例9—7。

例9—9（续例6—6）

我们用列联表方法分析过汽车销售记录分析问题，现在换用名义Logistic回归分析方法。

汽车销售商记录了其销售的303辆汽车的各项状况，包括购买者的性别、婚姻状况、年龄、国别、汽车尺寸、汽车车型，数据列在本书表6—8中（数据文件为：TBL_汽车销售.MTW）。

试分析销售“车型”与购买者年龄与国别有什么关系？

这里因变量“车型”取3个值：“家用”、“工作”、“跑车”。试建立由购买者年龄与国别预测“车型”概率的“名义Logistic回归方程”。因变量“车型”中我们选定的参考事件为“跑车”。

解　作为响应变量的“车型”有“家用”、“工作”及“跑车”三种，取某一值作为“参考事件”（默认时，计算机取拼音字母最后者作为“参考事件”，使用者可以自行指定参考事件），其他事件与参考事件构成比较对。使用指令“统计＞回归＞名义Logistic回归（Stat＞Regression＞Nominal Logistic Regression）”，得到的界面见图9—36。填写信息：“响应”填写“车型”；“模型”填写“年龄”和“国别”；“因子”填写“国别”。

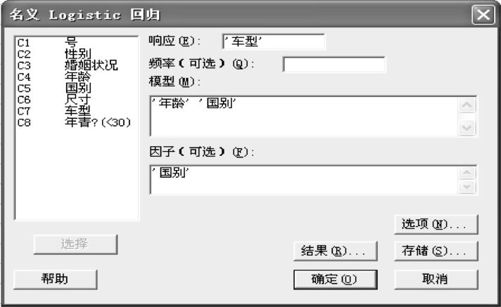
图9—36　名义Logistic回归操作图

计算后可得下列结果：

名义Logistic回归：车型与年龄，国别

响应信息

Logistic回归表

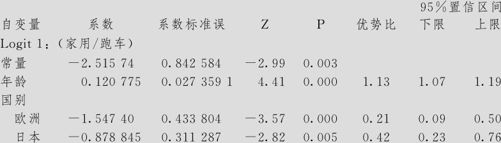
在上表中给出下列信息：

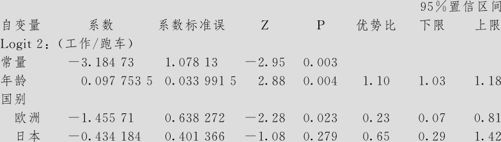
1．将“跑车”当作“参考事件”，其他两种车型都与“跑车”相比较。这里分了两组，第一组是“家用／跑车”；第二组是“工作／跑车”。

2．每组中共有3个变量，对于第一组“家用”与“跑车”相比，其方程为：

结果分析：（1）由Logistic回归表可见：“Logit 1：（家用／跑车）”以下部分是将“家用”与“跑车”相比的结果，由“系数”列可见，常数项β₁₀＝-2.51574，年龄的系数β₁₁＝0.120775，国别对于“欧洲”的系数β₁₂＝-1.54740，国别对于“日本”的系数β₁₃＝-0.878845，国别对于“美国”的系数是0。从而“家用”与“跑车”相比的回归方程如式（9—41）所示。

年龄为连续变量项，国别有三个取值（美国、欧洲及日本），以美国为基准项，欧洲及日本要分别加不同的截距系数。年龄系数0.120775为正，且p值为0.000，表示随年龄的增长，买“家用”的比率确实会有增加，年龄每增加1岁，买“家用”与买“跑车”二者的比率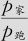会变为原来的e^0.1207＝1.128倍；另外，购车人是欧洲人或日本人则与购车人为美国人有显著不同，p值分别为0.000，0.005，截距项从大到小顺序依次为美国、日本、欧洲，说明选择购买家用车而非跑车，积极性的顺序是美国、日本、欧洲。换言之，美国人最爱购买家用车，欧洲人最爱购买跑车。

Logistic回归表

对数似然＝-281.997

检验所有斜率是否为零：G＝42.398，DF＝6，P值＝0.000

拟合优度检验

3．对于第二组“工作”车与“跑车”相比，其方程为：

比较买“工作”车与买“跑车”二者关系时，年龄系数0.09775为正，且p值为0.004，表示随年龄的增长，买“工作”车的比率确实会有增加，年龄每增加1岁，买“工作”车与买“跑车”二者的比率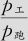会变为原来的e^0.09775＝1.103倍（增加得很少）；另外，购车人是欧洲人则与购车人为美国人有显著不同，p值为0.023；购车人是日本人则与购车人为美国人无显著不同，p值为0.279。截距项从大到小顺序依次为美国、日本、欧洲，说明选择购买工作车而非跑车，积极性的顺序是美国、日本、欧洲，美日差别不大。换言之，美国人最爱购买工作车，欧洲人最爱购买跑车。

4．总的回归效果是显著的，检验所有斜率是否为零：G＝42.398，DF＝6，p值＝0.000。同时拟合优度的检验也认为是没有问题的（两种拟合检验方法的p值都大于0.05）。

5．在第6章中，我们讨论了列联表的检验（6.3.1节），对于同样的例题（见例6—6），我们用卡方检验的方法，得到了显著性结论：选购汽车的类型确实与“年龄”有关，与“国别”也有关。但在卡方检验中只给出了定性的结论，究竟选购汽车的类型如何与“年龄”及“国别”相联系，只有到了名义的Logistic回归才有了定量的结论。当然，我们这里使用的年龄是连续变量数据，列联表只分了“年青”与“非年青”两类。工具不同，则要求的数据类型也不同，结论的细致程度也是不同的。

9.4.3　有序样本的Logistic回归

在9.4.1节讨论了响应变量取值只有“是”或“否”两类的二进制Logistic回归分析；在9.4.2节讨论了离散变量取名义值的情形。实际工作中，我们还会见到离散变量取有序值的情形，例如空气污染等级分为Ⅰ，Ⅱ，Ⅲ，Ⅳ共4个级别，这里Ⅳ级污染最重，Ⅲ级次之，Ⅱ级更好些，Ⅰ级最好，它们之间可以排出顺序。这就提供了比二值回归或取多个名义值这两种情况更多的信息。与响应变量有关的自变量可以是离散变量，也可以是连续变量，我们要建立回归方程，主要的工具仍然是二进制Logistic回归分析。以空气污染状况为例，我们可以先比较Ⅰ与Ⅱ，Ⅲ，Ⅳ；再比Ⅰ，Ⅱ与Ⅲ，Ⅳ；最后比Ⅰ，Ⅱ，Ⅲ与Ⅳ。这样比较了三次，就把所有可以配对的状况都比较清楚了。更详细点说是这样：在每次比较时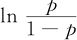，中的分子p代表的是“累积事件”出现的可能性，例如，第一次比较中，p代表的是出现Ⅰ级污染状况的概率与出现Ⅱ，Ⅲ，Ⅳ三级污染状况的概率1－p的比较；第二次比较中，p代表的是出现Ⅰ，Ⅱ两级累积污染状况的概率与出现Ⅲ，Ⅳ两级污染状况的概率1－p的比较；第三次比较中，p代表的是出现Ⅰ，Ⅱ，Ⅲ三级累积污染状况的概率与出现Ⅳ级污染状况的概率1－p的比较。将p理解为“累积事件”出现的可能性则可以更容易地理解有序状况的二进制Logistic回归分析。一般说来，如果有序观测值分为k级，则可以比较的共有k－1对。还应注意的是：这k－1对回归方程中，自变量的系数一定是相同的。

例9—10

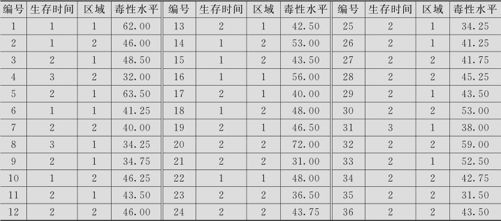
蝾螈生活在北半球温暖潮湿的淡水或沼泽地带，对环境要求很苛刻，在被污染的水中，寿命会大大缩短。将蝾螈的寿命分为3级：1级是小于10天；2级是介于10～30天；3级是31天以上。收集到的73只蝾螈来自1区或2区，而且记录了水中的毒性水平（见表9—15）。试分析蝾螈生存时间与水中的毒性水平及区域间的关系。

表9—15　蝾螈的生存时间数据表

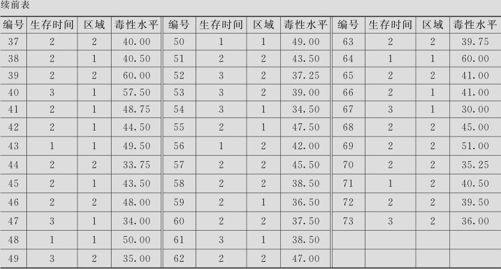
解　生存时间分为三级，它们是有顺序的，我们就可以分两次来比较。第一次，将1级与2，3级比，p代表的是出现最短寿命1级（＜10天）的概率，1－p代表的是出现较长寿命2，3级（≥10天）的概率；第二次，将1、2级与3级比，p代表的是出现较短寿命1，2级（≤30天）的概率，1－p代表的是出现最长寿命3级（≥31天）的概率。每次比较都使用二进制Logistic回归分析方法，而且这里使用的毒性水平的系数一定相同。具体的实现步骤使用者不必过问，计算机会自动进行分析。

使用指令“统计＞回归＞顺序Logistic回归（Stat＞Regression＞Ordinal Logistic Regression）”，得到的界面见图9—37。填写信息：“响应”填写“生存时间”；“模型”填写“毒性水平”和“区域”；“因子”填写“区域”。

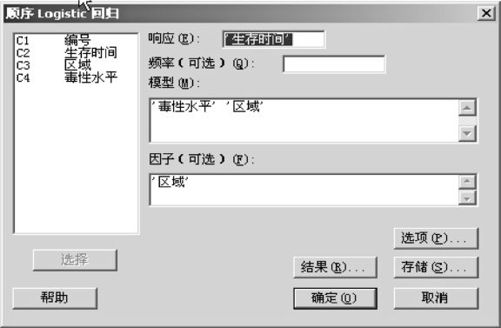
图9—37　顺序Logistic回归操作图

计算结果如下：

结果：REG_蝾螈.MTW

Logistic回归表

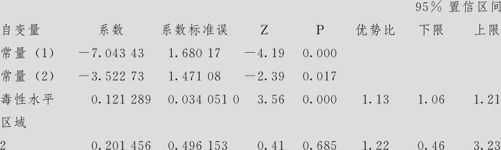
对数似然＝-59.290

检验所有斜率是否为零：G＝14.713，DF＝2，P值＝0.001

首先给出回归方程。我们这里分成两次进行：第一次，将1级与2，3级比，即“寿命＜10天”与“寿命≥10天”相比较；第二次，将1，2级与3级比，即“寿命≤30天”与“寿命≥31天”相比较。回归方程结果如下：

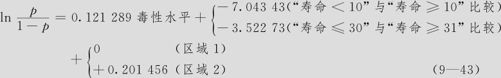
从计算结果还可以看出：回归的总效果是显著的，因为“检验所有斜率是否为零时，p值＝0.001”。对于“毒性水平”的影响，因为p值＝0.000，所以“毒性水平”是影响显著的；对于“区域”的影响，因为p值＝0.685，所以“区域”影响是不显著的。为此，应先删除“区域”因子，重新进行顺序Logistic回归。结果如下：

顺序Logistic回归：生存时间与毒性水平

Logistic回归表

对数似然＝-59.374

检验所有斜率是否为零：G＝14.546，DF＝1，P值＝0.000

拟合优度检验

相关性量度：（响应变量与预测概率之间）

首先给出回归方程。

这里的系数显著性检验中，毒性水平的p值＝0.000，说明毒性水平的效应是显著的；毒性水平每增加1级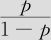，会变为原来的e^0.1199＝1.127倍，即出现1级“生存时间＜10天”的可能性与出现2，3级“生存时间≥10天”的优势比增加大约12.7％。相似的是，出现1，2级即“生存时间≤30天”的可能性与出现3级即“生存时间≥31天”的优势比增加大约12.7％。这也就是说，随毒性水平的增长，寿命短的概率越大。我们也可以从另一个角度来粗略地解释方程（9—44）的含义：

在方程（9—44）上方公式中，如果量值“0.119939毒性水平-6.86978”是负数（即毒性水平小于57.28），则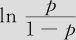会为负数，“生存时间＜10天”的可能性p将会小于“生存时间≥10天”的概率1－p，也就是说蝾螈的寿命多半会大于等于10天；同样在方程（9—44）下方公式中，如果量值“0.119939毒性水平-3.35691”是负数（即毒性水平小于27.99），则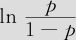会为负数，“生存时间≤30天”的可能性p将会小于“生存时间≥31天”的概率1－p，也就是说蝾螈的寿命多半会超过30天。这里的解释只是讨论了在三类寿命状况边缘处的状况，更细致的做法是，我们可以将给定的毒性水平代入式（9—44）中，准确地给出属于每种寿命状况的概率。

下面给出验算的结果。三组各有样本15，46及12个，任取一组的一个样本观测值可以与另两组的任一观测值配对，因此所有的搭配的“对”数共有n＝15×46＋15×12＋46×12＝1422对。对于这样一对属于不同寿命类型的观测值，分别将毒性水平代入回归方程（9—44），得出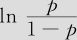值，比较其大小，若其顺序与观测的实际结果一致，则说明方程的预测结果与实际一致，即毒性水平越高则生存级别越低，记为“一致对”；若相反，则说明方程的预测结果与实际不一致，记为“不一致对”；如果毒性水平相等，则称这种情况为“结”。本例中，寿命属于“2类”的3号样本（毒性水平48.50）与寿命属于“3类”的4号样本（毒性水平32.00），分类与其毒性水平排序是一致的，因此是“一致对”；寿命属于“1类”的2号样本（毒性水平46.00）与寿命属于“2类”的3号样本（毒性水平48.50），分类与其毒性水平排序是不一致的，因此是“不一致对”；寿命属于“1类”的2号样本（毒性水平46.00）与寿命属于“2类”的12号样本（毒性水平也是46.00），分类不同但其毒性水平是相同的，因此是“结”。当然在本例要简单得多，自变量只有一个，而且回归系数为正，因此只要比较“毒性水平顺序”与“生存时间顺序”是否恰好相反就行了。

在1422对中，“一致对”为1115对，占总对数78.4％；“不一致对”为293对，占总对数20.6％；“结”为14对，占总对数1.0％；总效果还是不错的。

应用离散变量Logistic回归的问题很丰富，本书只是给出入门的介绍。