5.3　均值检验

在实际工作中，对均值的检验是最基本、最重要的。以下分单总体、双总体及多总体分别叙述之。

5.3.1　单正态总体均值检验

从第4章中的4.1节，我们知道了正态总体的抽样定理。对于单个正态总体，当总体标准差σ已知或σ未知的两种不同条件下，有关样本均值的抽样分布是不同的。

当总体标准差σ已知时，有公式：

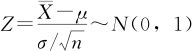
当总体标准差σ未知时，有公式（参见式（4—2））：

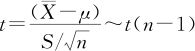
式中，S为样本标准差：

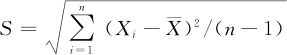
对于这两种不同的情况，分别进行介绍。

5.3.1.1　总体标准差σ已知

1．临界值法

我们这里分别给出不同备择假设下的拒绝域，实际检验时，根据计算出的检验统计量的观测值，看它是否落在拒绝域内，从而做出判断。

（1）关于总体均值μ常用的三对假设：

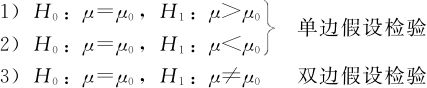
（2）检验统计量选择Z统计量。

在H₀成立时，Z～N（0，1）。

（3）对应这三个备择假设，它们各自的拒绝域分别为：

1）H₁：μ＞μ₀时，拒绝域是：

2）H₁：μ＜μ₀时，拒绝域是：

3）H₁：μ≠μ₀时，拒绝域是：

式中，Z_1－α是标准正态分布的1－α分位数。根据标准正态分布的对称性，Z_α＝-Z_1－α，因此，式（5—5）也可以写成下述形式（以后不再赘述）：

H₁：μ＜μ₀时，拒绝域是：

2．p值比较法

已知总体标准差时，通过MINITAB软件指令“统计＞基本统计量＞单样本Z（Stat＞Basic Statistics＞1-Sample Z）”来实现。

例5—2

从历史记录得知，快递公司投送从中国发往美国的邮件，平均投递时间为80小时，标准差为14小时。现随机抽取了28份邮件的投递时间记录见表5—2（数据文件：BS_投递时间.MTW）。

表5—2

可以看出平均值已降低为75.21小时。试用MINITAB分析发往美国的国际邮件的平均投递时间是否已低于80小时？取显著性水平α＝0.05。

解　许多统计问题的解决依赖于数据是否服从正态分布，我们这里要检验平均投递时间是否已低于80小时，必须先判定数据是否服从正态分布，在MINITAB中，指令“统计＞基本统计量＞正态性检验（Stat＞Basic Statistics＞Normality Test）”可以产生一个正态分布的概率图以及判定数据是否符合正态分布，正态检验的详细内容见5.3.1.3节。

假设目前我们已证明数据是服从正态分布的，且此处总体标准差已知，采用“单样本Z”进行总体均值假设检验。建立如下假设：

H₀：μ＝80

H₁：μ＜80

（1）选择“统计＞基本统计量＞单样本Z（Stat＞Basic Statistics＞1-Sample Z）”。

（2）输入已知的总体标准差“14”，输入待检验均值“80”，点击“选项（Options）”后，在“备择（Alternative）”选项中要输入“小于（Less Than）”，如图5—2所示。

图5—2　单样本Z检验操作图

（3）点击“图形（Graphs）”，选中“数据直方图”。

（4）点击“确定”后，得到输出结果（参见图5—3）。

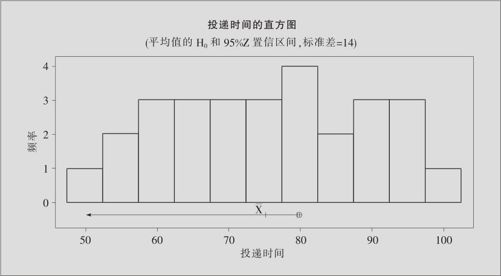
图5—3　投递时间的直方图

单样本Z：投递时间

mu＝80与＜80的检验

假定标准差＝14

（5）输出结果说明。

由图5—3可以看出，H₀：μ＝80在置信区间以外，或者由输出的p值＝0.035＜0.05，我们都可以得出同样的结论：发往美国的国际邮件的平均投递时间确实已低于80小时。

例5—3

抽查精细面粉的装包重量，其每包重量（单位：kg）在正常生产下均值为20，标准差0.1。某日在生产的产品中抽查了16包，其观测数据见表5—3（数据文件：BS_面粉重量.MTW）。

表5—3

现发现平均重量稍有变化，如果标准差不变，试问生产是否正常？取α＝0.05。

解　（1）建立假设：

H₀：μ＝20

H₁：μ≠20

（2）由于σ已知，故选用单样本Z检验。

（3）根据显著性水平α＝0.05及备择假设知拒绝域为：

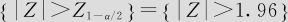
（4）由样本观察值，求得

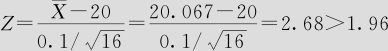
由于样本观察值落在拒绝域中，因此拒绝原假设，可以认为该天生产不正常。

应用MINITAB，打开“BS_面粉重量.MTW”数据文件，从“统计＞基本统计量＞单样本Z（Stat＞Basic Statistics＞1-Sample Z）”入口，填写变量名后，要特别注意在“选项（Options）”窗口选择双侧检验“不等于（Not Equal）”，如图5—4所示。

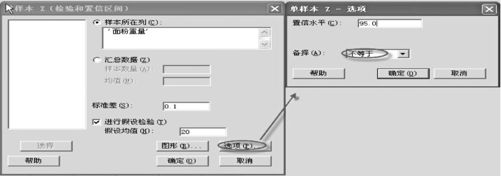
图5—4　单样本Z检验操作图

得到的结果如图5—5所示。

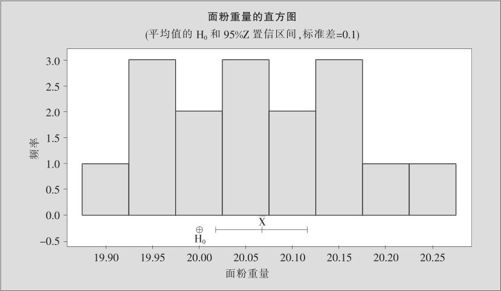
图5—5　面粉重量的直方图

单样本Z：面粉重量

mu＝20与≠20的检验

假定标准差＝0.1

输出结果说明：因为p值＝0.007＜0.05，故拒绝H₀，即认为面粉平均重量已有显著变化，生产不正常。换个角度考虑，由于观测的样本均值是20.0669，置信区间显示，以95％的把握断言，总体均值肯定落在（20.0179，20.1159），μ＝20未落入此置信区间，因而拒绝原假设。MINITAB还给出非常直观的图形（见图5—5）帮助判断：当H₀所对应的均值未落入均值的置信区间时，拒绝原假设；否则无法拒绝原假设。本例的结论是：拒绝原假设H₀，即面粉平均重量与20kg有显著差别，生产不正常。

5.3.1.2　总体标准差σ未知时

当总体标准差σ未知时，用σ的估计值S代替Z统计量中σ而得到t统计量。因此，相应各种检验方法与Z检验相似，只是把Z的标准正态分布换成t分布而已。

1．临界值法

我们这里分别给出不同备择假设下的拒绝域，实际检验时，根据计算出检验统计量的观测值，看它是否落在拒绝域内，从而做出判断。

（1）关于总体均值μ常用的三对假设：

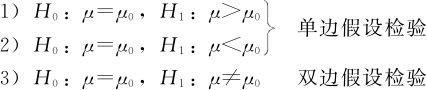
（2）当小样本（n＜30）时，用σ的估计S代替Z统计量中σ而得到t统计量：

在H₀成立条件下，t～t（n－1）。

（3）对应这三对假设，它们各自的拒绝域分别为：

1）H₁：μ＞μ₀时，拒绝域是：

2）H₁：μ＜μ₀时，拒绝域是：

3）H₁：μ≠μ₀时，拒绝域是：

式中，t_1－α（n－1）是自由度为n－1的t分布的1－α分位数，根据t分布的对称性，t_α＝-t_1－α，因此，式（5—10）也可以写成下列形式：

H₁：μ＜μ₀时，拒绝域是：

大样本（n≥30）时，上述检验统计量的拒绝域中的t分位数都可以近似用标准正态分布分位数来代替。

2．p值比较法

通过MINITAB软件指令“统计＞基本统计量＞单样本t（Stat＞Basic Statistics＞1-Sample t）”来实现。

例5—3续

与原题相同，只是不再假定总体标准差已知。

解　这时就应该用单样本t检验了。

（1）建立假设：

H₀：μ＝20

H₁：μ≠20

（2）由于σ未知，故选用单样本t检验。

（3）根据显著性水平α＝0.05及备择假设知拒绝域为：

（4）由样本观察值，求得

由于样本观察值落在拒绝域中，因此拒绝原假设，可以认为该天生产不正常。

应用MINITAB，打开“BS_面粉重量.MTW”数据文件，从“统计＞基本统计量＞单样本t（Stat＞Basic Statistics＞1 Sample t）”进入相关界面，填写变量名后，要特别注意在“选项（Options）”窗口选择双侧检验“不等于（Not Equal）”得到结果。

单样本T：面粉重量

mu＝20与≠20的检验

因为p值＝0.020＜0.05，拒绝H₀，即认为面粉平均重量已有显著变化，生产不正常。

例5—4

某车工所加工的轴棒要求平均长度为500mm，他在自己生产的轴棒中随机抽取了25根，测量结果得样本均值为501mm，样本标准差为1mm。问：在显著性水平α＝0.05下，他加工的轴棒长度均值能认为是500mm吗？

解　先建立假设：

H₀：μ＝500

H₁：μ≠500

由于是小样本，并且σ未知，故选用单样本t检验。

（1）选择“统计＞基本统计量＞单样本t（Stat＞Basic Statistics＞1-Sample t）”，输入“汇总数据（Summarized data）”，输入待检验的均值“500”，点击“选项（Options）”后，在“备择（Alternative）”选项中要输入“不等于（Not Equal）”。

（2）点击“确定”后，得到如下输出结果：

单样本T

mu＝500与≠500的检验

（3）输出结果说明。计算结果显示：＝501，S＝1，t＝5，而t_1－α/2（n－1）＝t_0.975（24）＝2.064（t分布分位数表），由于|t|＝5＞2.064，故拒绝H₀。

同样，由于MINITAB输出的p值＝0.000＜0.05，因此我们的结论是：拒绝原假设，即在显著性水平α＝0.05下，不能认为加工的轴棒长度均值是500mm，它已经超长了。

在这里我们要提醒读者，应该深入理解检验结果的含义。有人会问：原来标准差为1mm，平均值与标准值之差也是1mm，这个差别不过是1倍标准差，怎么这样小的差别就被判为差异显著了呢？问题出在现在讨论的是样本平均值而不是样本的单值。根据中心极限定理，原来的标准差为1mm，25个样品的平均值的标准差降为原来的1/5了，也就是说平均值的标准差只有0.2mm了，这样一来，偏离值1mm相当于5倍标准差了，差异当然是显著的了。

将上述结果列在表5—4中以便查用，通常将用Z，t作检验统计量的检验分别称为Z检验和t检验。

表5—4　单个正态总体均值的显著性水平为α的检验

5.3.1.3　单总体均值检验所需要验证的条件

是否对任何数据都可以进行单样本Z检验或单样本t检验呢？当然不是。在检验前，我们必须验证所有数据同时符合下列两个条件：

（1）数据观测值是相互独立的；

（2）数据必须服从正态分布。

为了检查这两个基本前提是否成立，应该对此分别进行检验。

1．独立性检验

由于我们讨论假设检验的基础是：我们所收集的数据是来自同一总体的随机独立样本，因此对于来自同一总体的样本数据的独立性检验，通常采用游程（run，也译为“链”、“串”）检验来进行。

依时间或其他顺序排列的有序数列中，具有相同的事件或符号的连续部分称为一个游程，常常记r为游程总个数。比如：

此游程数为r＝6。

我们要检验的独立性若写成假设检验的形式，则应该这样设立假设：

H₀：数据是相互独立的

H₁：数据不是相互独立的

从游程的概念出发，很容易看出，当数据是相互独立的时候，数据的出现顺序完全随机，因此，游程的个数应该不多不少。但是如果像证券市场中的上证指数那样，第一天指数很高，第二天指数接着也会很高；第一天指数很低，第二天指数接着也会很低，这就必然导致游程的个数偏少，这是典型的数据不独立的例子。另一种类型是：如果将球往地上一个筐内投掷希望命中，第一次投远了，即投掷距离太长，第二次肯定要矫枉过正用力小些，导致投得偏近，即投掷距离太短；反之，这次投近了，即投掷距离太短，下一次肯定要矫枉过正用力大些，导致投得偏远；这样一来，每次都在矫正，游程总个数会偏多。总之，游程总个数偏少或游程总个数偏多都是数据不独立的表现。为此我们可以对游程总个数设定拒绝域：游程总个数偏少或游程总个数偏多。具体计算方法比较复杂，在样本量较小（小于40）时，有临界值表可查（见本书附表10）；在样本量较大时，可以使用正态近似，计算机软件可以直接算出结果。

从MINITAB中的“统计＞非参数统计＞游程检验（Stat＞Nonparametric＞Runs Test）”可以进行游程检验。它可以用来检验样本的独立性，也可用来检验任何序列的随机性，而不管这个序列是怎样产生的。但使用此检验的条件是要在大样本情况下才行，在大样本情况下，游程个数可以近似认为是正态分布。另外，它在操作中也有个小缺点，那就是要手工输入中位数才行，它的默认功能是以平均值为界进行游程检验，而独立性检验必须以中位数为界进行游程检验。因此，样本量较小时可以用计算机算出游程总个数，但要查表来判断是否拒绝。总之，游程检验要按照样本量的大小分以下两种情形进行：

（1）当样本量不超过40时。设立如下假设：

H₀：数据是相互独立的

H₁：数据不是相互独立的

用“统计＞质量工具＞运行图（Stat＞Quality Tools＞Run Chart）”可以给出游程总个数r的计算结果，然后查附表10确定下临界值R₁及上临界值R₂。当r≤R₁或r≥R₂时，则拒绝原假设。

例5—5（续例5—3）

在面粉重量例题中有16个数据（数据文件：BS_面粉重量.MTW）。问：上述数据是否为相互独立的？

解　建立如下假设：

H₀：数据是相互独立的

H₁：数据不是相互独立的

由于样本量不超过40，先求出游程总个数r。

（1）选择“统计＞质量工具＞运行图（Stat＞Quality Tools＞Run Chart）”（见图5—6）。

图5—6　小样本游程计算操作图

（2）输入变量，选定“子组大小（Subgroup Size）”为1，点击“确定”后，得到如图5—7所示输出结果。

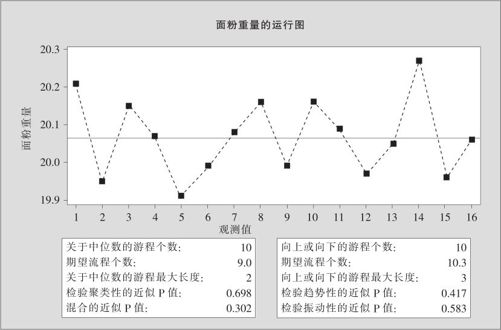
图5—7　小样本游程计算结果图

（3）输出结果说明。由输出知道，关于中位数的游程总个数为10。我们的样本量为16，以中位数为界，则比它高的（记为“+”号），比它低的（记为“-”号）各为8个。查附表10的左上角表，对应n₁＝8与n₂＝8的交汇点得到临界值R₁＝4；查附表10的右上角表，对应n₁＝8与n₂＝8的交汇点得到临界值R₂＝14。如果游程总个数小于等于4或游程总个数大于等于14，则拒绝原假设，说明数据不独立。现在游程总个数r＝10，未落入拒绝域中，所以结论是：无证据显示独立性有问题，因此，在目前抽样条件下，可以认为（或者说也只能认为）面粉重量的数据是独立的。

（2）当样本量超过40时。由于附表10的应用范围是n₁，n₂小于等于20，即总样本量小于40才行。当总样本量超过40时，虽然无临界值表可查，但这时可以对游程总个数用正态近似了。设立如下假设：

H₀：数据是相互独立的

H₁：数据不是相互独立的

先求出中位数，再以中位数为界，用“统计＞非参数统计＞游程检验（Stat＞Non-parametric＞Runs test）”求出游程总数，并用正态近似法计算出p值，当p值小于α时，拒绝原假设。

实际上，样本量超过25时已经可以使用正态近似方法了，因此在数据量位于25～40之间时，查表的精确计算法与正态近似方法二者都可用。下面我们先用正态近似方法来计算。

例5—6（续例5—2）

检验快递公司的投递时间是否独立（数据文件：BS_投递时间.MTW）。问此投递时间数据是不是独立的？

解　建立如下假设：

H₀：数据是相互独立的

H₁：数据不是相互独立的

（1）用“统计＞基本统计量＞图形化汇总（Stat＞Basic Statistics＞Graphical Summary）”，求出观测数据的中位数是“76”。

（2）选择“统计＞非参数＞游程检验（Stat＞Nonparametrics＞Runs Test）”，输入变量及分界值（观测数据中位数）“76”，如图5—8所示。

图5—8　游程检验操作图

（3）点击“确定”后，得到如下输出结果：

游程检验：投递时间

投递时间　游程检验

游程高于及低于的分界值K＝76

观测到的总游程数＝11

期望的总游程数＝15

14个观测值高于K，14个低于

P值＝0.123

输出结果说明：由于游程检验输出的p值＝0.123＞0.05，所以不能拒绝原假设，在现有抽样结果条件下可以认为投递时间数据是独立的。

对此数据也可以直接用精确计算方法。游程总个数为11，查附表10可以得知其接受域为（9，21），结论同样是可以认为数据相互独立。

最后，根据上述所得到的数据独立性结论，该采取什么行动呢？

如果发现数据是独立的，则可以继续进行数据的正态性检验等后续工作步骤。如果发现数据不是独立的，建议仅能使用运行图展示数据采集结果的状况，可以使用点估计值（point estimates）来估计参数，但不要计算置信区间上下限，不要进行假设检验。在这种情况下，最重要的任务不是讨论如何进行后面的分析，而是首先搞清楚为什么数据会出现不独立的情况。通常这是由于在收集数据过程中混入了某个因子的系统性影响，必须先把它找出来，然后设法去除它的影响，并重新收集数据、重新进行分析。

2．正态性检验

许多统计问题的解决依赖于数据是服从正态分布的，因此我们必须先判定数据是否服从正态分布。

例5—7

以例5—3数据为例（数据文件：BS_面粉重量.MTW）介绍如何进行正态检验。

解　打开数据文件：BS_面粉重量.MTW，建立原假设和备择假设：

H₀：面粉平均重量服从正态分布

H₁：面粉平均重量不服从正态分布

（1）选择“统计＞基本统计量＞正态性检验（Stat＞Basic Statistics＞Normality Test）”。

（2）在“变量（Variable）”栏中输入C1列，在“标题（Title）”栏可输入自定义的标题，如图5—9所示。

图5—9　正态检验操作图

对话框中列出了三种正态性检验的方法：

1）Anderson-Darling（AD）检验：根据观测数据的累积分布函数ECDF（empirical cumulative distribution function）来计算，它是默认选项。一般统计学者都认为此方法是目前所有正态性检验中功效最高者。

2）Ryan-Joiner检验：类似Shapiro-Wilk检验（简称W检验）。在正态概率纸上，如果数据服从正态分布，则数据点形成一条直线，本方法是以讨论数据点的横纵两个坐标间的相关系数为基础的检验方法。显然，相关系数越接近于1则代表数据点形成的线“越直”。此方法的优点是它可以对很小的样本量进行正态检验。此方法被国际标准化组织ISO及我国标准化委员会采纳作为正态性检验的方法。

上述两种方法检验功效差不多。

3）Kolmogorov-Smirnov（KS）检验：根据观测数据的累积分布函数ECDF与理论分布相差的最大值处的差别来进行检验的一种方法，它适用于多种分布，因此单独针对正态分布的检验功效比前两种专门方法要低一些。

要说明的是，这三种检验方法所设定的假设都是一致的——原假设：数据服从正态分布；备择假设：数据不服从正态分布。如果我们对同一组数据同时采用这三种方法检验会有什么结果？一般来说，它们的结论应该是一致的。如果结论不一致，那又该如何判断呢？这种情况确实是可能发生的。这时，根据我们前面所叙述的假设检验基本概念：“拒绝是有说服力的，接受是没有说服力的”，因此，只要有任何一种检验方法的结果是判定拒绝原假设，那么我们的结论都应该是拒绝原假设，即这组数据不服从正态分布。

（3）点击“确定”后，得到输出结果如图5—10所示。

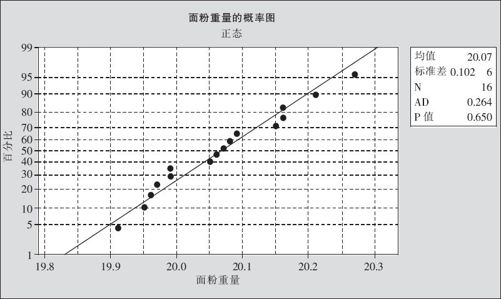
图5—10　面粉重量正态概率图

（4）输出结果说明。由于输出的p值＝0.650＞0.05，因此我们的结论是：没有足够证据拒绝原假设，即在目前情况下，接受数据服从正态分布的原假设。

数据正态性检验的结果在另一处也可以看到：选择“统计＞基本统计量＞图形化汇总（Stat＞Basic Statistics＞Graphical Summary）”。由图5—11我们可以看到输出的p值，判定方法跟此处相同，只是没有图5—10这样的概率图输出罢了。

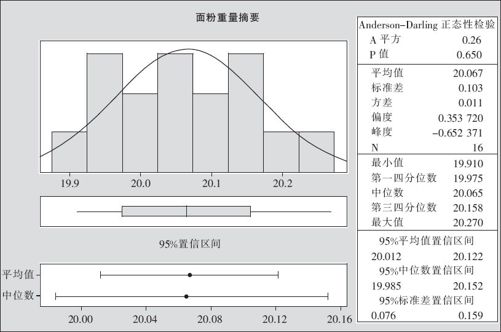
图5—11　图形化汇总正态检验结果图

在生产过程或社会生活中，常常遇见正态分布，这不是偶然的。概率理论中，有理论说明正态分布形成的机理：如果一个变量的波动是由大量的微小而且独立的随机因素的积累而形成，则它一定是个正态随机变量。这里一是强调“大量”，二是强调每个因素的影响都“微小”。例如以固定角度、固定初速度打出炮弹，其弹着点应该是固定的一个点，但实际上，炮弹的飞行距离受太多因素的影响，而每个因素的影响又足够小，因此弹着点就会形成正态分布，我们平时遇见的很多量在理论上讲它就应该是正态分布。但有些量却并不如此，例如金属的疲劳寿命、社区中家庭月收入等，肯定不是正态分布的。

这里有几点需要澄清。

“生产过程是稳定的”与“生产特性服从正态分布”有什么关系？二者应该没有关系。在生产过程是稳定的条件下，其生产特性有可能并不服从正态分布；反之，生产特性服从正态分布，其生产过程也可能并不稳定。二者是从两个不同角度来讨论问题的。

“数据是相互独立的”与“生产特性服从正态分布”有什么关系？二者也应该没有关系。数据是相互独立的说明其采样过程正常，但数据相互独立时生产特性仍可能为非正态分布；反之，生产特性服从正态分布也并不能保证数据的采集是相互独立的。独立性与正态性二者也是从两个不同角度来讨论问题的。

对于数据非正态该如何处理？这在假设检验中是个很常见的情况。一般说来，数据如果是正态分布，则我们可以使用在书中通常所介绍的，例如Z检验、T检验等方法；如果数据非正态分布就不能用这些方法，而应该换用非参数检验方法。关于非参数检验方法，我们将在第7章中详细介绍。

如果平时的生产状况一直是正态分布，某一天突然变成非正态了，那就应该找寻出现非正态分布的原因；如果平时的生产状况一直是非正态分布，那么这就是“正常状况”，无须采取什么措施非要让它成为正态。以后我们还会学到一些内容，例如在残差分析中，本该是正态分布的，如果出现非正态该怎么办？这种事一般是没有固定的方法予以解决的。正如问“一个人发烧了，这该如何医治？”好的医生会说，一定要找出发烧的原因，然后对症下药才能退烧；只有庸医才会说，吃些退烧药就行了。如果本身确实该是正态，而现在非正态了，这就反映出某种“不正常”的状况，是一种“征兆”，但是原因可能多种多样，找到形成非正态的根本原因才是解决问题的根本途径。

数据非正态在正态性检验中会出现什么状况？数据如果是正态的，则应该在正态概率图（见图5—10）上散点呈现直线的形状；数据如果不是正态的，则散点应该在正态概率图上呈现出并非直线的形状。正态概率图上散点的形状完全反映了分布的形状。在3.2.3节分布形状的分析中，介绍了分布形状度量指标：偏度和峰度。大家都知道，正态分布的偏度和峰度都恰好为0。对于非0的偏度、峰度的状况，图5—12介绍了它们的直方图及概率图之间的对应关系。

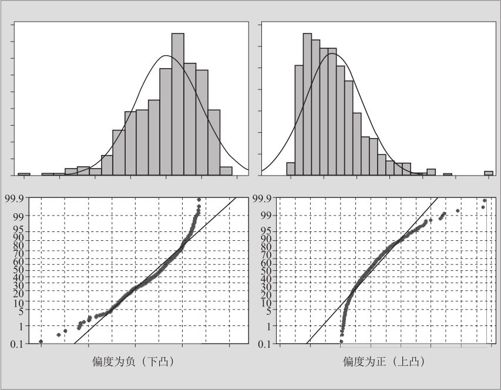
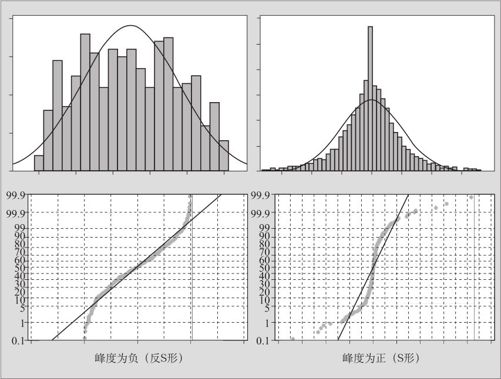
图5—12　非正态分布的直方图与概率图

下面我们再给出一例，说明由于取值精度不够导致“非正态”的情况。

在本书例12—1中，在生产线上收集了共125个钢球的直径数据（见表12—3）（数据文件：SPC_钢球直径.MTW）。当测量结果记录为3位小数时，数据呈现为正态分布，正态性检验也获得通过（p值为0.216），见图5—13上图；但将此数据取整为仅保留2位小数时，则未能通过正态性检验（p值为0.005），见图5—13下图。

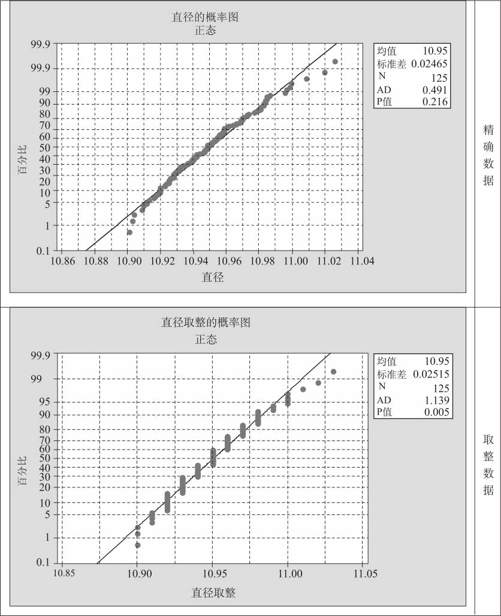
图5—13　由于精度不够导致的非正态分布图

总之，按照自然规律，有些量就应该服从正态分布，有些量则不然。判断一个随机变量是否为正态分布是很重要的。对于非正态分布的各种具体状况应该有更深入的理解。

5.3.2　双正态总体均值检验

要对双正态总体均值进行检验，需要分别从这两个正态总体中抽取样本。这时要特别注意的是：抽取的两组样本是独立的还是配对的。若从两个总体中抽取出的样本观测值彼此互不影响，抽取的样本量也可以不同，则这样的样本是普通的独立样本；若选取的样本观测值是成对的，即是对选定的一组个体，分别观测在两种处理之后的结果，则称这样的样本为配对样本。

例如，厂商声称新眼药水比老眼药水治疗红眼病疗效显著，为了检验这种说法，可以采用两种方法。方法1：选取30名红眼病患者，随机选取其中15人，让每个人用老药水，其余15人用新药水，过7天后加以比较，这就是普通的独立样本。方法2：选取15名红眼病患者，让每个人一只眼睛用老药水，另一只眼睛用新药水，过7天后两个眼睛间加以比较，这就是配对样本。可以看到，配对样本中能充分去除掉除药水以外的其他干扰因素的影响，即可以控制个体间由于年龄、健康状况等其他因素带来的差异。两种不同的样本抽取方法要用不同方法加以处理，在抽样前就要分辨清楚。我们先讨论普通的独立样本的分析，配对样本留在5.3.2.2节讨论。

5.3.2.1　双正态总体均值检验

设有两个总体，X～N（μ₁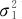，），Y～N（μ₂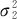，），从总体X中抽取的样本X₁，X₂，…，X_n，样本均值为，样本方差为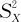，样本标准差为S_X，从总体Y中抽取的样本为Y₁，Y₂，…，Y_m，样本均值为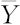，样本方差为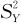，样本标准差为S_Y。

要讨论的检验问题是下列三种：

（1）H₀：μ₁＝μ₂，H₁：μ₁＞μ₂

（2）H₀：μ₁＝μ₂，H₁：μ₁＜μ₂

（3）H₀：μ₁＝μ₂，H₁：μ₁≠μ₂

以下分三种情况来讨论。

1．σ₁，σ₂已知

当σ₁，σ₂已知时，可以采用检验统计量

在H₀成立，即μ₁＝μ₂时，Z～N（0，1）。

对检验问题（1）H₀：μ₁＝μ₂，H₁：μ₁＞μ₂，拒绝域为{Z＞Z_1－α}。

对检验问题（2）H₀：μ₁＝μ₂，H₁：μ₁＜μ₂，拒绝域为{Z＜-Z_1－α}。

对检验问题（3）H₀：μ₁＝μ₂，H₁：μ₁≠μ₂，拒绝域为{Z＞Z_1－α/2}。

2．σ₁，σ₂未知，但σ₁＝σ₂

当σ₁，σ₂未知，但σ₁＝σ₂时，可以采用检验统计量：

式中

在H₀成立条件下，t～t（n＋m－2）。

对上述三个检验问题的拒绝域可以用t分布的分位数得到，它们分别是：{t＞t_1－α（n＋m－2）}，{t＜-t_1－α（n＋m－2）}，{|t|＞t_1－α/2（n＋m－2）}。

3．σ₁，σ₂未知，且不知道σ₁＝σ₂

当σ₁，σ₂未知，且不知道σ₁＝σ₂（或确实知道二者不等时），可以采用近似双样本的t检验，其统计量为：

其自由度ν取最接近于下列数值ν的整数：

在实际工作中，第一种情况几乎不会出现，MINITAB也没有相应窗口，我们在此不再讨论。工作中对于第二种情况应用最多，我们通常称之为双样本的t检验。注意，能够使用双样本的t检验的条件共有三项：

（1）两组样本内相互独立，两组间也相互独立；

（2）两组数据皆来自正态分布总体；

（3）两个总体方差（或标准差）相等，。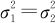

请大家特别留意这三项基本前提。对于前两项的含义及检验方法，我们已在5.3.1.3节中作了介绍。这里要特别注意第3项条件，我们应该充分理解这样要求的合理性。事实上，如果两批数据精度悬殊（例如一批螺钉直径用卡尺量，另一批螺钉直径用千分尺量），两批数据其实是不可比较的。双样本的t检验就提出了这种要求。如果它不能满足，则我们用统计量（5—16）来检验时，它只可能是一种近似的双样本的t检验方法罢了，其总自由度已经大打折扣，精确度受到很大的影响。另外，这里要求是两个总体方差（或标准差）相等，并没要求两个样本方差（或标准差）相等。实际工作中，两个样本方差（或标准差）有些差别并不奇怪，它是被允许的。至于如何通过两批样本数据来检验两总体的方差是否相等，请参考5.4.2节。

虽然在MINITAB软件中，比较两总体均值时，无论两总体方差是否相等计算机都可以计算，但必须明确：选定“假定两总体方差相等”时，计算机进行的是精确的双样本t检验，而未选定“假定两总体方差相等”时，计算机进行的只是近似的双样本t检验。

将上述关于两个总体均值的显著性水平为α的检验列在表5—5中，同样用检验统计量Z，t的检验分别称为Z检验和t检验，但由于双样本Z检验很少使用，所以MINITAB软件没有此窗口。

表5—5　两正态总体均值的显著性水平为α的检验

例5—8

一家冶金公司需要减少其排放到废水中的生物氧需求量（Biochemical Oxygen Demand，BOD）含量。用于废水处理的活化泥供应商建议，用纯氧取代空气吹入活化泥以改善BOD含量（此数值越小越好）。在两种处理的废水中，空气法抽了10个样品，氧气法抽了9个样品，数据见表5—6（数据文件：BS_生物氧需求量.MTW）。

表5—6

已知BOD含量服从正态分布，问在显著性水平α＝0.05下，该公司是否应改用氧气来减少BOD含量？

解　建立假设：

H₀：μ₁＝μ₂

H₁：μ₁＞μ₂

式中，μ₁，μ₂分别代表空气和氧气条件下的BOD含量。

（1）选择“统计＞基本统计量＞双样本t（Stat＞Basic Statistics＞2-Sample t）”。界面如图5—14所示。

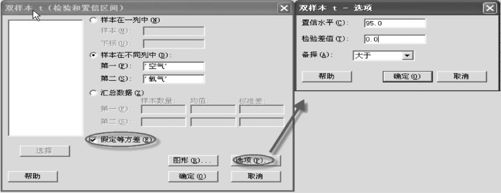
图5—14　双样本t检验操作图

（2）在经过检验后，可以判定两总体方差相等（具体过程见例5—13），所以勾选“假定等方差（Assume equal variances）”，点击“选项（Options）”后，因为显著性水平为0.05，故在“置信水平（Confidence level）”输入“95”（％），在“备择（Alterna-tive）”选项中要输入“大于”。

注意，图5—14中数据录入方式有三种：

1）Samples in one column：两组样本数据输入在同一列内，但必须有另一个变量来分辨，称为识别列，用Subscripts（下标）来标识。

2）Samples in different columns：两组样本数据分别在不同的列。

3）Summarized data：汇总数据。

（3）点击“确定”后，得到如下输出结果：

双样本T检验和置信区间：空气，氧气

空气与氧气的双样本T

差值估计：16.61

差值的95％置信下限：2.44

差值＝0（与＞）的T检验：T值＝2.04　P值＝0.029　自由度＝17

两者都使用合并标准差＝17.7356

（4）输出结果说明。由于输出的p值＝0.029＜0.05，因此我们的结论是：拒绝原假设，使用氧气确实能显著减少BOD含量。

例5—9（续例4—8）

假定A，B两名工人生产相同规格的轴棒，关键尺寸是轴棒的直径。由于A使用的是老式车床，B使用的是新式车床，二者精度可能有差异。现他们各测定了13根轴棒的直径（数据见例4—8，数据文件：BS_轴棒直径.MTW）。试分析A，B两名工人生产的轴棒直径的均值相等吗？

解　建立如下假设：

H₀：μ₁＝μ₂

H₁：μ₁≠μ₂

式中，μ₁，μ₂分别代表工人A及B生产的轴棒直径。

在检验均值的相等性之前，先要检验其方差的相等性（见例5—14），结果是断言二者方差并不相等。此后，按例5—8中所叙述的方法完全相同的操作，在图5—14的左半部界面内，注意不要勾选“假定等方差”，右半部界面内，勾选“不等”，则可以得到下列结果：

双样本T检验和置信区间：A，B

A与B的双样本T

差值估计：1.965

差值的95％置信区间：（0.435，3.496）

差值＝0（与≠）的T检验：T值＝2.71　P值＝0.015　自由度＝17

结论是：二者轴棒直径间有显著差异。值得注意的是，原来各自有13个观测值，双样本t检验自由度应该是24，但现在由于方差不相等，对方差特大者缩小其权重，加权平均得到了方差的估计量，最终只剩下17个自由度。

5.3.2.2　配对样本的检验

配对检验在实际工作中时常会遇到。比如，考察某种减肥药品的药效，如果用完全不同的两批人，一批未吃药，一批吃药，将此类问题当作两总体的均值检验问题，则很容易得到“疗效不显著”的结论，这是因为不同人的体重本身有很大差异，而这种误差并不是由于药物疗效引起的，减肥药的疗效就被淹没在误差之中了。解决此问题最好的办法是收集成对数据的方式：对同一批人，先记录原始体重，再记录吃药后的体重，这样将每个人服用药物前后的体重进行比较，把同一人服用药物前后的两个结果之差求出来（求出吃药后的“体重减少量”d，此数可能为正也可能为负），这就可以较准确地度量出药效在每个人身上产生的作用。最后进行的检验就是：看“体重减少量”d的均值是否为正数。设X_i和Y_i是第i个人减肥前后的体重，则d_i＝X_i－Y_i（i＝1，2，…，n）是第i个人的体重减少量，记μ为体重减少量d的均值，则我们要检验的问题变成：H₀：μ＝0，H₁：μ＞0。

一般情况下的配对检验，就是对于差值的均值μ进行单总体的假设检验，其具体形式可能有下列三种情况：

H₀：μ＝0，H₁：μ＞0

H₀：μ＝0，H₁：μ＜0

H₀：μ＝0，H₁：μ≠0

显然，这些都是单个正态总体均值是否为0的检验问题。

另外，通常情况下，σ是未知的，因此对此问题用单样本的t检验，在MINITAB的入口是：“统计＞基本统计量＞单样本t（Stat＞Basic Statistics＞1-Sample t）”检验，检验统计量变成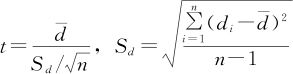。在显著性水平为α时，拒绝域可参见式（5—9）至式（5—11）。

当然，在MINITAB中，我们还可以省略求出差值d的步骤，直接用“统计＞基本统计量＞配对t（Stat＞Basic Statistics＞Paired t）”，即配对t检验来对两列原始数据直接进行检验。

例5—10

想要比较某种减肥药物的疗效，选定10个人进行实验，收集了每个人服用减肥药前后的体重数据，表5—7是测量数据的记录（数据文件：BS_配对t检验.MTW）：

表5—7　体重测量记录

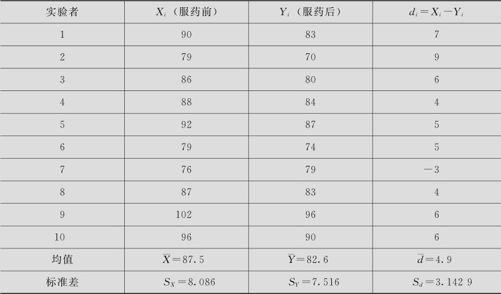
问：在α＝0.05水平上，服用药物后体重是否有显著的降低？

解　建立假设：

H₀：μ＝0

H₁：μ＞0

这里的数据属于成对数据，求出“体重减少量”d，令d_i＝X_i－Y_i（i＝1，2，…，10），便是每个人服用药物后体重减少量，n＝10，在α＝0.05时的拒绝域是：

{t＞t_1－α（n－1）}＝{t＞1.833}

由于n＝10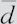，＝4.9，S_d＝3.1429，可求得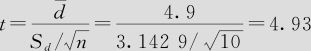，样本统计量落在拒绝域中，所以可以认为服用药物后体重有显著的降低。

用MINITAB软件，打开“BS_配对t检验.MTW”数据文件，选择“统计＞基本统计量＞单样本t检验（Stat＞Basic Statistics＞1-Sample t）”检验，对于差值进行单样本均值是否大于0的检验，得到下列结果：

单样本T：d＝x－y

mu＝0与＞0的检验

p值＝0.000＜0.05，拒绝原假设，即服用药物后体重有显著的降低。

当然这里也可以直接采用配对t检验。

解　建立假设：

H₀：μ＝0

H₁：μ＞0

（1）选择“统计＞基本统计量＞配对t（Stat＞Basic Statistics＞Paired t）”；

（2）在“列中的样本（Samples in columns）”栏输入数据所在列，点击“选项（Options）”后，因为显著性水平为0.05，故在“置信水平（Confidence level）”输入“95”（％），在“备择（Alternative）”选项中要输入“大于”（见图5—15）。

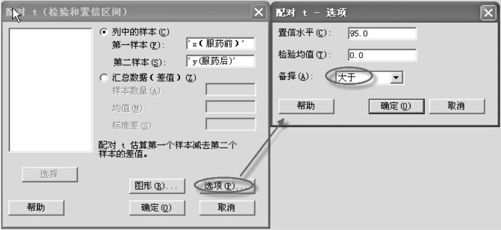
图5—15　配对t检验操作图

（3）点击“确定”后，得到如下输出结果：

配对T检验和置信区间：x（服药前），y（服药后）

x（服药前）－y（服药后）的配对的T

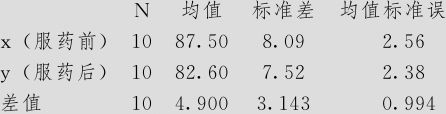
95％平均差下限：3.078

平均差＝0（与＞0）的T检验：T值＝4.93　P值＝0.000

（4）输出结果说明。p值＝0.000＜0.05，拒绝原假设，即服用药物后体重有显著的降低。

由此可见，我们对差值采用单样本t检验与对原始数据直接采用配对t检验结论是一致的。

如果将此问题误认为是普通的两样本均值检验，我们将使用MINITAB软件直接用“统计＞基本统计量＞双样本t（Stat＞Basic Statistics＞2-Sample t）”检验，得到下列结果：

双样本T检验和置信区间：x（服药前），y（服药后）

x（服药前）与y（服药后）的双样本T

差值估计：4.90

差值的95％置信下限：-1.15

差值＝0（与＞）的T检验：T值＝1.40　P值＝0.089　自由度＝18

两者都使用合并标准差＝7.8063

p值＝0.089＞0.05，不能拒绝原假设，即服用药物后体重没有显著降低。可见对于事先设计好的配对观测数据进行分析，可以得到较为精确的结论；若误当作普通两样本数据来分析，则容易犯第二类错误而得不到正确结论。