2.4 常用的离散分布
在实际工作中可能用到很多离散分布,但其中最常用的离散分布有二项分布和泊松分布两种。MINITAB包含了这两种分布,一共列出了7种离散分布。本书则再加上理论讨论时常用的0—1分布,因此一共列出下列8种分布,括号内的英文是MINITAB软件中所使用的简称。
(1)0—1分布(0—1 distribution)
(2)二项分布(binomial distribution)
(3)Poisson分布(Poisson distribution)
(4)超几何分布(hypergeometric distribution)
(5)几何分布(geometric distribution)
(6)负二项分布(negative binomial distribution)
(7)整数均匀分布(integer distribution)
(8)任意离散分布(discrete distribution)
下面分别给出简要介绍。
2.4.1 0—1分布(两点分布)
有一种试验,每次试验只有两种可能的结果,而且出现两种结果的概率都保持不变。两种结果的例子很多,比如正面与反面,合格与不合格,通过与不通过,命中与不命中,具有某特性与不具有某特性等,我们归纳而统称为“成功”与“失败”。至于验收产品时,什么叫“成功”,大多数人倾向于把出现不合格叫做“成功”。记“成功”出现的概率为p,失败出现的概率为1-p,则称此随机变量服从0—1分布,也称为两点分布,记为B(1,p)。写成分布律的形式则如表2—8所示。
表2—8 0—1分布的分布律

容易得出其期望及方差是:

0—1分布在理论讨论上很重要,但实际应用很少。又因为下面介绍的二项分布当n=1时就成为0—1分布,即二项分布是以0—1分布为其特例的,所以在MINITAB软件中并未专门列入此种分布。我们只要理解式(2—55)的结果就够了。
2.4.2 二项分布
考虑从本厂产品中随机抽取20件进行检测,产品只分一等品和二等品。根据历史数据知,产品的二等品率为20%,那么20件产品中大约会抽出几件二等品?如果记二等品件数为随机变量X,它的分布律会是怎样的?
把上述问题一般化:假设我们独立地进行了n次试验(“独立”就是说,上次试验的结果不影响下次试验的结果),每次试验结果只有“成功”及“失败”两种结果,而且每次试验获得“成功”的概率都是固定的常数p,记“成功”的总次数为随机变量X,则称X的分布为二项分布(记作X~B(n,p))。本节开头的问题就可以描述为:进行了20次抽样试验,抽中二等品产品称为“成功”,每次“成功”概率都是常数p=0.2,总“成功”次数的分布就是参数为n=20,p=0.2的二项分布,即X~B(20,0.2)。数学上可以证明一般的二项分布的取值概率为:
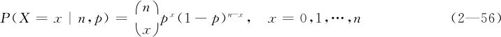
容易得出二项分布的期望及方差是:

用MINITAB软件可以求出所有的概率值,而且可以画出分布律的图形。
在MINITAB中打开一个新(空白)文件。在第一列上命名为“次数”,取值为0,1,…,20。为此,从“计算>生成模板化数据>简单数集(Calc>Make Patterned Data>Simple Set of Number)”入口,就会看见信息窗如图2—52所示。
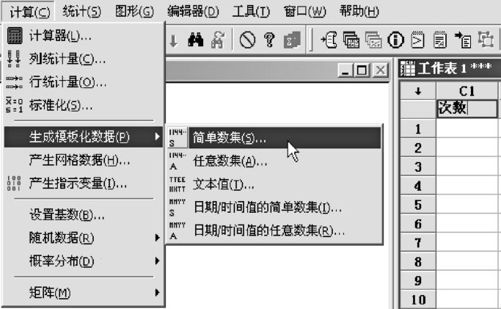
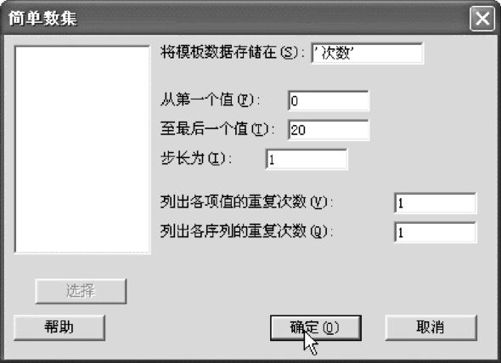
图2—52 形成规则数据序列操作图
只要在“从第一个值”填入“0”,只要在“至最后一个值”填入“20”,“步长”保持为原来的“1”,则可以形成所需数列。再从“计算>概率分布>二项(Calc>Probability>Binomial)”入口,就会看见信息窗如图2—53所示。
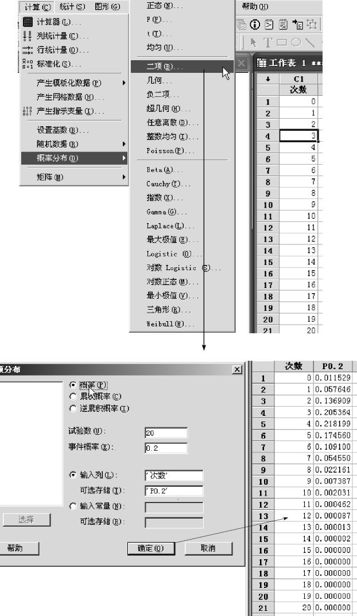
图2—53 形成二项分布概率分布律操作图
在已知分布律时,这里有两种方法可以绘制其图形,其中散点图方法,在2.1节已有介绍。下面介绍对于离散型指定分布类型后的分布律绘制方法,其实这与连续分布的图形绘制是完全一样的。
从“图形>概率分布图(Graph>Probability Distribution Plot)”入口,选中“单一视图(Single Parameter)”即可,其操作示意参看图2—26。
在分布类型中选定“二项(Binomial)”,再指定相应参数(见图2—54)即可。
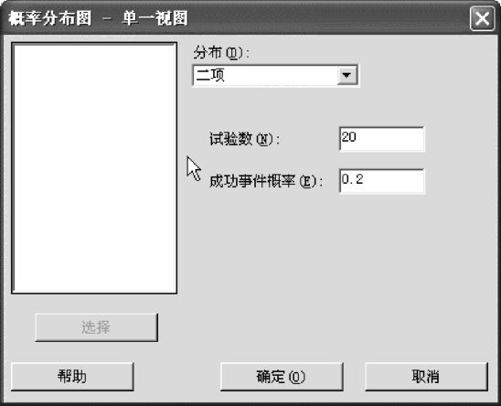
图2—54 绘制二项分布概率分布律图的参数设定
这时可以得到如图2—55所示的结果。
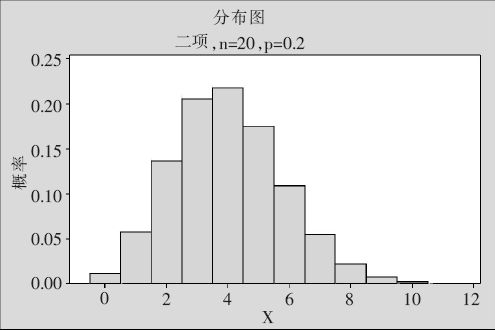
图2—55 二项分布概率分布律图的输出结果
从图中可以看出,当x=4时,概率值最大;当x<4时,概率值逐渐增长;当x>4时,概率值逐渐减小,很快就几乎为0了。从实际经验上,大家早有这种粗略的理解:如果二等品出现的概率是0.2,则在抽出的20件产品中,发生“二等品出现0件”这样的好事,概率大约1/100(百里挑一);发生“二等品出现20件”这样的倒霉事,概率也绝对不会超过百万分之一。
二项分布除了作为连续生产过程中不合格品数的精确分布外,当抽样的样本量小于有限总体其个体总数的10%时,还可以作为超几何分布的近似分布。
虽然现在有了计算机可以帮助我们计算复杂的二项分布概率,但我们仍然应该了解有关二项分布的一些规律性的概念。在二项分布的计算中,最重要的是它的正态近似。当二项分布中的参数n足够大(比如超过100),参数p不是太大或太小(0.1<p<0.9),则二项分布B(n,p)近似于正态分布N(np,np(1-p))。
例2—9
一个城市出生10000名婴儿,假定生男生女概率相等,市长对每个男婴赠给一个小足球,对每个女婴赠给一个芭比娃娃,问市长要准备多少足球和芭比娃娃才能保证万无一失?
所谓“万无一失”指的是失误的概率小于万分之一。如果保证“永无一失”那就一定要准备1万个足球和1万个芭比娃娃。但实际上不用准备这么多,因为出现这种极端情况的概率几乎为零。
记男婴出生人数为X,则可知X~B(10000,0.5)。由于二项分布当样本量足够大(超过100),p不是太大或太小,因此可以用正态分布近似。由于均值为μ=np=5000,σ2=np(1-p)=2500,因此σ=50。故B(10000,0.5)与N(5000,502)近似相同(见图2—56)。
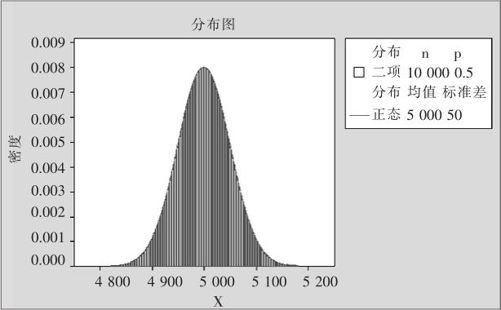
图2—56 二项分布的正态近似示意图
从图2—30下方列出的表中,可以得知,在均值μ两侧的4σ范围内,将包含全部数据的99.9937%,4σ范围之外即未被包含部分之概率不到十万分之七,即未超过万分之一。在本问题中,4σ=200,所以X落入(4800,5200)之外的概率不到万分之一,所以市长要准备5200个足球和5200个芭比娃娃足可以保证万无一失。
注意上面的解释一定不要理解为百分比的概念。上例中,保证万无一失的范围4σ=200,相对原来总人数n=10000占“2%”就够了。其实这样理解是完全错误的。读者可以自己计算,如果n=100万,则4σ=2000,只占n的2‰;而当n=100时,4σ=20,占n的2/10。可见,n越大,则随机现象的规律性越明显,随机波动会显得越小;n越小,则随机现象的规律性越不明显,偶然性就越大,随机波动会变得很大。而个别的随机现象是绝对不可预报的。有人声称可以预报彩票的中奖号码,稍有概率论常识的人都会知道这是无稽之谈。关于二项分布的规律性问题,我们在第6章比率检验中还会更深入地讨论。
2.4.3 Poisson分布
在自然界中,常常有一些不寻常的事情出现,例如,2006年福州遭到4次台风的袭击,一片镀防腐蚀膜的机翼上出现了3个瑕疵点,一匹染了蓝色的布上有5个黑斑点,等等。这种稀有事件的出现有什么规律性?概率论的理论研究结果表明,在一定的条件下,这些稀有事件出现的概率都服从Poisson分布(泊松分布),大量的观测也证明了这一点。博尔德希维兹(Bortkewitsch)在1898年提交了一份报告,记录了1875—1894年的20年间普鲁士骑兵团被马踢伤致死的士兵人数,发现其分布与Poisson分布非常吻合;英国著名物理学家卢瑟福观测记录了放射性物质在7.5秒内放射出的α粒子数目,其分布与Poisson分布非常吻合;第二次世界大战中,德国用V-2飞弹袭击伦敦,将伦敦分为576个区,发现每个区的真实弹着点数分布与Poisson分布非常吻合;在照片上记录细菌群的分布,每个细菌会形成小黑点,将显微镜整个视野分成若干小方块后,各方块中黑点的个数也服从Poisson分布。这些都不是偶然的。在质量管理中也常遇到这样的情况,我们不仅要关注不合格品,而且要关注每件产品中所包含的不合格项的情况。例如,在芯片的生产中,记录每片芯片上的瑕疵点数,则瑕疵点数就应该服从Poisson分布。记X为不合格点数,如果X的分布律为:

则称X的分布为Poisson分布,记为X~P(λ)。
容易得出Poisson分布的期望与方差为:

不要小看上述公式,它是有特殊含义的:期望值一定与原观测值有相同量纲,方差的量纲一定是原观测值的平方,这二者怎么可能相等呢?世上的分布成百上千,有此性质的分布唯有Poisson分布。仅从量纲上看,由于量纲与量纲的平方竟然相同,此量纲一定是无量纲的常数,即“点数”、“件数”、“次数”等。任何带有实际物理量纲者(如长度、重量等)绝不可能是Poisson分布。
Poisson分布与二项分布有非常深刻的本质上的联系。在二项分布中,当n较大(超过100)时,如果p值很小(p<0.05,且np<30),则二项分布B(n,p)可以近似看成是Poisson分布P(np)。比如,一条高速公路上,每天车流量为n=10000,发生车祸的概率是p=0.0003,这时,np=3,也就是说,每日在此高速公路上将平均发生3次车祸。如果略去n和p的具体数值,只是笼统地说“每日在此高速公路上平均发生3次车祸”,这也就是Poisson分布P(3)。对于这种实际问题,用两种分布模型去处理,结果几乎是一样的。用MINITAB很容易计算出车祸问题的结果(见表2—9),两行结果中的上一行是用二项分布计算的,下一行是用Poisson分布计算的,可以看出,二者数值几乎相同。
表2—9 二项分布与Poisson分布比较表

Poisson分布应用广泛,可以用来描述不少随机变量的分布。例如,中午时分,快餐店中每分钟顾客到来的人数;一定时间内,接错电话的次数;一定时间内,某操作系统发生的故障数;一个铸件上的缺陷数;一平方米玻璃上的气泡数;一件产品擦伤留下的痕迹数;一页书上的错字数,等等。
从Poisson分布的概念出发还可以看出下列性质,这就是均值的“可分性”。如果每罐稻米中的稗子数服从均值为6的Poisson分布,那么很容易想到,如果以半罐作为一“小罐”,每小罐稻米中的稗子数应服从均值为3的Poisson分布;若1000平方米一匹的化纤布平均瑕疵点数是25,瑕疵点数的分布是P(25),4平方米可以缝制一套工作服,每套工作服的瑕疵点数的分布就应该是P(0.1)。这就是说,在单位换算(例如从“罐”到“小罐”)时,Poisson分布的性质不变,而且均值也可以做同样的换算,当然这里只限于被分割或被合并的总份数很少的情况才成立。
2.4.4 超几何分布
当总体只包含有限个个体时,即使仍然只有两种可能的结果,但前次抽样的结果会影响下次抽样的结果。例如,原来只有100件产品,其中6件不良。抽第一件,不良率显然是6/100。但若第一次抽到良品,则第二次抽样的不良率就变成6/99;但若第一次抽到不良品,则第二次抽样的不良率就变成5/99。这时模型就与二项分布有很大的不同了。如果我们设想抽完第一次后,将样本放回,它可能被再次抽到,这种“有放回”的抽样将产生二项分布;如果我们抽完第一次后,不将样本放回,这种“无放回”的抽样将产生的分布称为超几何分布。假设总体中有N个个体,其中M个个体具有特征A(比如“不良”),在从中随机地抽出n(n≤N)个个体中(无放回抽样),恰好取得x个具有特征A的元素的概率为:
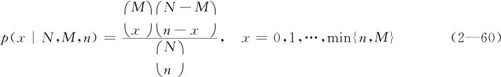
超几何分布在抽样理论中占有重要地位。另外,超几何分布与二项分布之间有密切联系。事实上,当总体中元素的数量N很大,而取出的元素n相对较小时(n≤0.1N),这种差别就应该很小,前次抽样的结果基本上不会影响下次抽样的结果。超几何分布包含三个参数N,M,n(n≤M)。
超几何分布的数学期望和方差分别为:
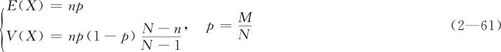
2.4.5 几何分布
如果我们进行独立试验时仍然只有“成功”和“失败”两种结果,而且每次获得“成功”的概率都是p,但试验一直要进行到首次出现“成功”为止,记所需试验次数为X,则X的分布称为几何分布(geometric distribution)。表面看来,这种模型与二项模型相同,但其实不然:二项分布的条件是试验次数固定,试验中总成功次数X为随机变量;现在则是试验次数为随机变量,而且最后一次一定是“成功”(否则早出现“成功”试验将停止)。这时得到的分布律为:

式中,x表示获得首次“成功”所需要的总次数。几何分布具有一条重要特性——无后效性,即在前n次试验中未出现成功的条件下,再经过m次试验(即在第n+m次试验中)首次出现成功的条件概率,等于首次成功恰好需要进行m次试验的无条件概率。换句话说,在已经进行了n次试验,且未出现成功时,首次成功恰好需要再进行m次试验的概率与以前的试验无关,就像试验重新开始一样。在老虎机前等待中大奖,究竟能否中大奖与你在此老虎机前已经投了多少次硬币是无关的,在另外一台机器上去碰碰运气和在此“死等”效果是相同的。在离散型随机变量中,只有几何分布才具有无后效性。这个分布只包含一个参数p(0<p<1)。
几何分布的数学期望和方差分别为:

该公式的解释其实也很自然,如果你打枪命中概率是0.1,你进行射击直到首次命中为止,则平均说来你得打上10枪才行。注意这里说的并不是“打了10枪,平均会命中一枪(这是二项分布)”;现在是打到首次命中为止,前面射击各枪肯定是都没命中,最后一枪一定是命中,这才是几何分布,这时很可能要打上20枪、30枪才行。其分布律图形见图2—57,右边尾巴拖得很长。

图2—57 几何分布的分布律图
2.4.6 负二项分布
讨论和几何分布相同的模型:如果我们进行独立试验时仍然只有“成功”和“失败”两种结果,而且每次获得“成功”的概率都是p,但试验一直要进行到“成功”出现r次为止,记所需试验次数为X,则X的分布称为负二项分布(negative binomial distribution),也称Pascal分布。这里要注意,负二项分布与二项分布截然不同:二项分布时,试验次数是固定的,试验中出现成功的次数X为随机变量;负二项分布则是总“成功”次数给定,总试验次数为随机变量,而且一定是最后一次为“成功”(否则早就达到r次出现“成功”,试验将停止)。这时得到的分布律为:
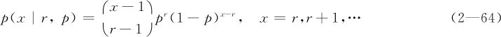
负二项分布中包含两个参数r,p(r≥1,0<p<1)。
在实际中,负二项分布常用于不幸事件和发病情况等问题的统计推断。负二项分布的数学期望和方差分别为:

容易看出,负二项分布中如果r=1,则变成了几何分布,也就是说,几何分布是负二项分布的特殊情况。
2.4.7 整数均匀分布
整数均匀分布是在M到N的整数范围内,以等概率取值的分布。本来其英文全称应该是Integer Uniform Distribution,但MINITAB对名称作了简化。其概率分布为:
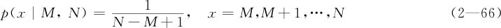
这个分布包含起点和终点M及N共两个参数。
整数均匀分布的数学期望和方差分别为:

2.4.8 任意离散分布
离散型随机变量的分布有很多种,除了上述常用的著名的分布外,其他的离散型分布的分布规律就要用自行定义的表格来实现了。表格的样子如表2—6所示,一般离散随机变量分布律表都要写成这种形式。具体说来,我们在本章最开始举的例子,其分布写成这样(原表见表2—3,这里重复列出):
质量等级分布状况表

我们可以以此分布来进行分析、生成随机数等,也可以画出分布律图(见图2—1或图2—4),这些就不再讨论了。
为了使读者查阅方便,我们把2.3节和2.4节中所有叙述过的结论,加上三个导出分布(t分布,卡方分布,F分布),一起用表格的方式加以汇总。这就是下面给出的表2—10。
表2—10 常用分布的密度公式及数字特征表


