5.5　单因子ANOVA分析

假如六西格玛团队遇到了这样一个问题：考察温度对某一化工产品得率的影响。选了五种不同的温度进行试验，希望判断温度对化工产品得率是否有显著影响。这就是多总体的均值比较问题。前面几节我们介绍了双正态总体均值的检验方法，对于多个正态总体均值的检验，是否可以采用先前学过的方法逐一两两检验总体均值是否相等呢？答案是否定的。因为比较过程将更加复杂（比如，若有n个总体，则需要检验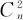次），还会导致判定结果犯第一类错误的概率大大增加。

以三个总体均值相等的检验为例，采用先前学过的方法，分别对两总体均值相等性进行检验，需要进行三次检验，若每次检验的置信水平为0.95，那么三次检验后，置信水平将降低为0.95³＝85.7％。总体数目越多，置信水平将越低，第一类错误风险将变得太大，这将使得这种比较方法不再具有实际价值。为此，我们引入一种更为有效的方法来实施多总体均值相等的检验，这就是方差分析（analysis of variance，ANOVA）。

5.5.1　单因子ANOVA分析基本原理

为讨论方便，将试验中要考察的结果称为指标，将在试验中会改变状态的因素或对指标有影响的因素称为因子，通常用大写字母A，B，C等表示。因子在试验中所处的不同状态（各因子在其变化范围内所处的具体状态）称作因子的水平，用表示因子的字母加下标来表示，譬如因子A的水平用A₁，A₂，…表示。如果一项试验中，只有一个因素变化，其他因素不变的话，这种试验称作单因子试验。最简单的多总体均值相等性检验其实就是单因子试验问题。下面通过一个实例说明方差分析的基本原理。

例5—15

考察温度对烧碱产品得率的影响，选了4种不同的温度进行试验，在同一温度下进行了5次试验（见表5—12，数据文件：ANOVA_单因子.MTW）。希望在显著性水平α＝0.05下，判断温度对烧碱产品得率是否有显著影响。

表5—12

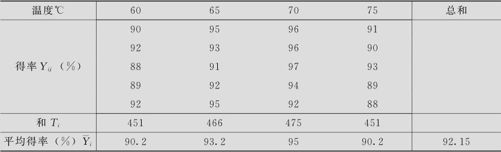
上述表中数据Y_ij的含义是：Y的两个下标中的前者i代表总体号，第二个下标j为观测值号，i＝1，2，…，k；j＝1，2，…，m_i。

首先，从例5—15可以看到，即使在同样的温度下，产品得率也不一样，这是因为虽然外界条件基本相同，但由于随机因素的干扰，结果会有微小的波动。我们可以假定，在一定的温度下，产品得率有一个理论上的均值，实际观测数据对理论均值的偏离是随机误差，这个误差一般会服从正态分布。但温度不同时，各产品得率应该有不同的均值，这些均值上的差异是由于不同的温度造成的，是系统误差。由于除了温度以外的其他因素尽可能保持一致，因此可以认为每个温度下对应的总体方差相同。这样，现在解决的问题就变为对于4个均值不同、方差相同的正态总体，推断（因子）温度对（指标）烧碱产品得率影响是否显著的问题，等价于推断4个方差相同的正态总体均值是否相等的问题。

把上述说明推广到一般情况，即

（1）正态假定：假定因子有k个水平，每一水平下均服从均值为μ_i（i＝1，2，…，k），方差为σ²的正态分布，每一水平下的指标全体便构成一个总体，共有k个总体；

（2）等方差假定：因子在每一水平下所服从的正态分布方差相等；

（3）数据独立性假定：对于第i个水平下收集的数据Y_ij（j＝1，2，…，m_i）是相互独立的；

（4）在这三个假定成立的前提下，检验如下假设是否为真：

H₀：μ₁＝μ₂＝…＝μ_k

H₁：至少一对μ_i≠μ_j

下面具体说明分析的思路：如果在不同温度下，烧碱产品平均得率差异与随机误差相比不相上下，那么可以认为不同温度下的烧碱产品得率间没有显著差别。反之，如果在不同温度下，烧碱产品平均得率间的差异与随机误差相比显得较大，那么这种差异就很难用随机误差来解释，只能认为是由于“温度不同”这个原因造成的。

下面来看看如何对这些差异进行定量描述。

把同样温度下的试验作为一组，用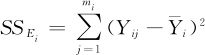来表示本组（水平）内数据间的随机误差大小，求出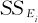之和来表示总的随机误差，记为SS_E，称SS_E为组内离差平方和（或误差平方和）。

对于不同温度下产品得率的差异用SS_A来表示，称SS_A为组间离差平方和。

再考虑所有数据的总离差平方和SS_T：

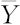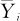这里，是的平均值。

数学上可以证明，这三者间有下列等式成立：

这就是著名的平方和分解公式。

方差分析的基本思想就是求出组间离差平方和SS_A与组内离差平方和SS_E之比值。此比值越大，说明因子效应越显著；反之，说明因子效应越不显著。为了消除数据个数及分组数（水平数）的多少给离差平方和带来的影响，在求此比值时，还要除以各自的自由度，得到各自的均方和MS_A，MS_E，这个比值就称为F统计量。换言之，F统计量就等于MS_A/MS_E。而其中MS_A＝SS_A/df_A，MS_E＝SS_E/df_E。

检验的基本思想就是：若F值足够大，则可以判定因子是显著的。具体写出来则是：如果F＞F_1－α（df_A，df_E），则可以判定因子是显著的。与此同时，还可以得到如下结果：

（1）第i个水平指标的均值的估计为：；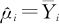

（2）各组内的共同的误差方差σ²之估计值是MS_E。

将上述分析内容用一个表格来归纳，就得到了下列方差分析表（见表5—13）。其中关键的是检验统计量F，MINITAB软件还在最后给出了与F值相对应的p值。

表5—13　单因子方差分析表

如果F＞F_1－α（df_A，df_E），则拒绝H₀，表示不同水平下的指标的均值确有显著差异，此时称因子效应是显著的，否则称因子效应不显著。

具体求解例5—15。在例5—15中，要考察4种温度，在显著性水平取α＝0.05时，判断温度对烧碱产品得率是否有显著影响，下面是手工计算的具体过程。

Y_ij：表示第i水平下第j个试验数据

m：表示因子在每一水平下试验的次数（这里各水平试验次数相同，故省略了下标）

k：表示因子水平数

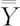：总的平均值

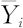：因子在第i水平下的平均值

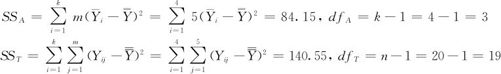
SS_E＝SS_T－SS_A＝56.4，df_E＝n－k＝20－4＝16

MS_A＝SS_A/df_A＝84.15/3＝28.05

MS_E＝SS_E/df_E＝56.4/16＝3.52

F＝MS_A/MS_E＝28.05/3.52＝7.96

临界值F_1－α（df_A，df_E）＝F_0.95（3，16）＝3.24

把以上计算结果列入单因子方差分析表（见表5—14）。

表5—14　单因子方差分析表

由于F＝7.96＞3.24，因此拒绝原假设。结论：不同温度对烧碱产品得率有显著影响。

在用MINITAB软件计算时，步骤如下：

（1）打开“ANOVA_单因子.MTW”数据文件，要注意的是：如果数据录入格式是C1，C2列形式（即响应变量在一列，因子水平代码在另一列）时，从“统计＞方差分析＞单因子（Stat＞ANOVA＞One way）”进入相关界面（见图5—20左）；如果数据录入格式是C4－C7形式（即因子各水平对应的响应值在不同的列），就从“统计＞方差分析＞单因子（Stat＞ANOVA＞One way（Unstacked））”进入相关界面，如图5—20右所示。

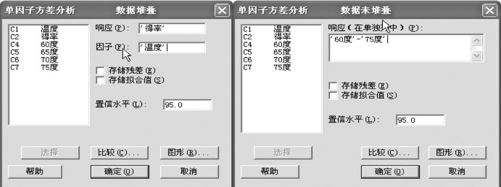
图5—20　ANOVA分析（数据堆叠和未堆叠）操作图

（2）输入数据所在列后，因为显著性水平为0.05，故在“置信水平（Confidence Level）”输入“95”（％），点击“图形（Graphs）”后，勾选“数据箱线图”，如图5—21所示。

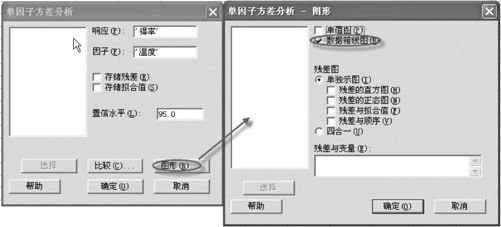
图5—21　ANOVA分析（数据堆叠）生成数据箱线图

（3）点击“确定”后，得下列输出结果及图5—22：

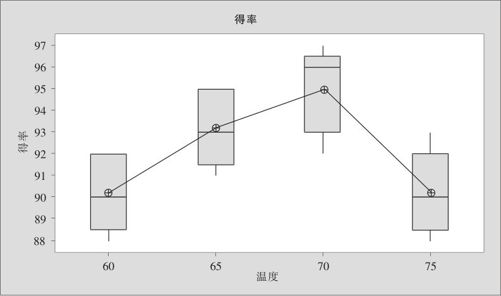
图5—22　得率与温度的箱线图

单因子方差分析：得率与温度

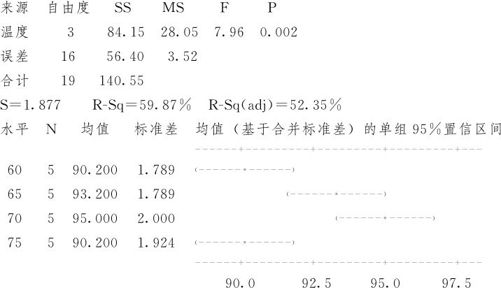
合并标准差＝1.877

（4）输出结果的解释。由于p值＝0.002＜0.05，因此拒绝原假设。结论：不同温度下烧碱产品平均得率有显著差异。在ANOVA第一步得到的ANOVA表中，如果p值＞0.05，无法拒绝原假设，说明各水平间并无显著差异，则方差分析到此结束。如果p值＜0.05，拒绝原假设，说明各水平间有显著差异。这时就提出了下一个问题，哪些水平间有显著差异，哪些水平间没有显著差异？这就需要了解各水平下平均值的差异的详细情况，这就是下段的内容：如何分析多重比较的结果。

注意：在ANOVA表下方用文字打印方式输出了一个均值置信区间的示意图，但此图仅提供了均值状况的参考示意，并不能用来作为两总体间是否有显著差异的任何评比根据。

在ANOVA的计算过程中也输出了4种不同温度的箱线图。从中可以看出，70℃时得率似乎最高。但我们同样不能由此图得到任何确定性的论断。如何进行更细致的比较请看下节。

5.5.2　单因子ANOVA分析多重比较方法

当因子显著即因子在各水平下均值有差异时，我们可以进一步了解因子在k个水平下均值的差异，即同时检验如下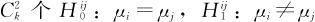假设，这个检验叫做多重比较。

进行多重比较方法的关键是如何选定第一类错误风险值的问题。MINITAB给出了如下四种多重比较方法的风险值设定方式供我们选择，下面分别说明。

（1）“Tukey，整体误差率”：Tukey方法所设定的所有的两两检验总和起来的整体误差率，栏框中默认的是整体误差率5（％），输入值若大于1，MINITAB会解释为百分比。显然，如果整体误差率设定为5％，那么两两比较检验的第一类错误设定的风险要远远低于5％。Tukey方法可以计算所有多重比较（两两均值差）的置信区间。以后我们在实际进行单因子的方差分析时，一定只选Tukey算法，以保证整体误差率为5％。

（2）“Fisher，个别误差率”：采用Fisher方法计算多重比较（两两均值差）的置信区间时，所设定的是两两比较的每次检验的第一类错误都为5％，这样一来，整体第一类错误的误差率肯定会大大超过5％。以后我们在实际进行单因子的方差分析时，除非有特殊需要，一定不选Fisher算法。

（3）“Dunnett，全族误差率”：它讨论的是另一种试验问题，在这种试验中，存在一个特殊的称为“对照组”的总体。2005年，我国在完成了SARS疫苗的各项动物实验鉴定后，决定对SARS疫苗进行实际的人体试验，当时将36名勇敢的试验者等分为三组，一组注射生理盐水，此组称为“对照组”（control group），另两组分别注射1倍和2倍SARS疫苗。这时我们要进行的只是将注射1倍和2倍SARS疫苗组与对照组相比较，以确认SARS疫苗是否有效，其他组之间不再进行比较。采用Dunnett方法计算的是其他各数据组与控制组平均值差异的置信区间。计算前当然先要特别指定哪组是“对照组”。除非我们进行的是这种对照试验，否则也不会选择此方法。

（4）“许氏MCB，全族误差率”：它讨论的是对于各组只进行与最佳组的比较分析，其他组与组之间并不进行比较。当然这里又要分平均值是越大越好（Largest is best）还是平均值越小越好（Smallest is best）这两种类型。采用许氏MCB方法将计算每一个水平平均值与整体最好的平均值之差异的置信区间。此方法用得也不多。

将以上四种多重比较方法的特性归纳如表5—15所示：

表5—15　多重比较法对比表

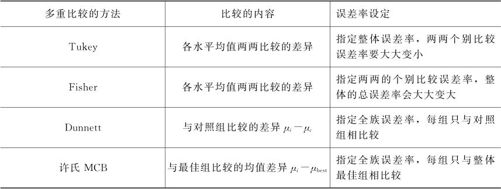
注：μ_i为第i水平下的均值；μ_c为控制组水平下的均值；μ_best为整体最好水平下的均值。

例5—16（续例5—15）

考察4种温度，在显著性水平取α＝0.05时，判断温度对烧碱产品得率是否有显著影响。在前段，我们已判断出各水平间有显著差异（其操作见图5—20、图5—21）。下面分析：哪些水平间有显著差异？哪些水平间没有显著差异？

解　前面已介绍了方差分析表中ANOVA的计算及箱线图的绘制。在得到各组间差异显著的结论后，我们可以进行多重比较的检验。

从“统计＞方差分析＞单因子（Stat＞ANOVA＞One way）”进入相关界面后，点击“比较（Comparisons）”，如图5—23所示。

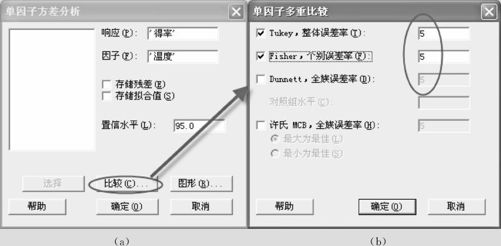
图5—23　ANOVA多重比较操作图

选中Tukey算法，设定整体误差率为5％。

再选中Fisher算法，设定个别误差率为5％（注意：本次选定该项只是为了进行两种算法比较，显示一下结果。以后再也不要选此项）。

点击“确定”后，得下列输出结果：

使用Tukey法对信息进行分组

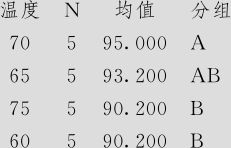
不共享字母的均值之间具有显著差异。

Tukey95％整体置信区间

温度水平间的所有配对比较

单组置信水平＝98.87％

温度＝60减自：

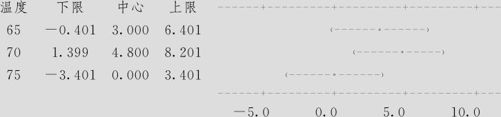
温度＝65减自：

温度＝70减自：

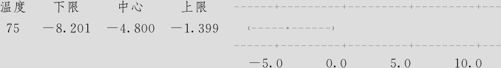
我们先看Tukey方法的三组多重比较的置信区间：

由于Tukey方法所设定的整体误差率是5（％），显然，两两比较检验的第一类错误设定的风险要远远低于5％。输出中指明：“95％整体置信区间，温度水平间的所有配对比较，单组置信水平＝98.87％”，这就意味着，在两两比较中，第一类错误概率只有1－98.87％＝1.13％。

Tukey方法可以计算所有多重比较（两两均值差）的置信区间。以后在实际进行单因子的方差分析时，一定只选Tukey算法，以保证整体误差率为5％。

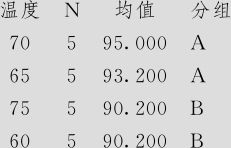
在以下的分析中，大家应该参看图5—22中的不同温度下得率的箱线图。图中显示出：温度为70时得率最高，65时稍差，60及75时更差些。

第一组以水平一（温度60）作被减项，其他水平65，70，75时的均值分别减去水平60时的均值得到的置信区间。从65减去60时的样本均值为3.0，但总体的均值差可能大些，也可能小些，但我们以98.87％的把握可以断言，总体的均值差将落入（-0.401，6.401）内，可以看出这个置信区间包含0，说明温度60与65间总体的均值差不排除为0，也即二者得率平均值无显著差异。其实从上述分析可以看出，我们对于两总体的均值差将落入什么区间的具体数值并不关心，关键是这个区间是否包含0，也就是区间的上下限是否恰好正负符号相反。如果上下限皆为正，则说明第二个总体均值比第一个总体均值大；如果上下限皆为负，则说明第二个总体均值比第一个总体均值小。从这组中可以看出，只有一组均值差异显著：从温度70减去60时的样本均值为4.8，但总体的均值差以98.87％的把握将落入（1.399，8.201）内，上下限皆为正，故温度70均值肯定超过温度60均值。我们记为“70度＞60度”。

同样分析，第二组以水平二（温度65）做被减项，其他水平70，75时的均值分别减去水平65时的均值得到的置信区间都包含0，故温度为70和75时，得率平均值与温度65无显著差异。

第三组以水平三（温度70）做被减项，温度75时的均值减去水平70时的均值得到的置信区间，可以看出这里所有的置信区间（-8.201，-1.399），上下限皆小于0，说明温度75时，得率平均值比温度为70时小。我们记为“75度＜70度”。

总之，Tukey方法计算结果中，一共有两组均值差异显著，那就是：“70度＞60度”及“75度＜70度”，其余各组间并无显著差异。在R16新增的对信息进行分组的结果中，也可以看出，70度及65度为A，75度及60度为B，二者差异显著。

以下是Fisher算法结果：

使用Fisher方法对信息进行分组

不共享字母的均值之间具有显著差异。

Fisher95％两水平差值置信区间

温度水平间的所有配对比较

同时置信水平＝81.11％

温度＝60减自：

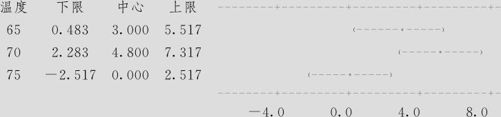
温度＝65减自：

温度＝70减自：

由于Fisher方法所设定的个别误差率是5（％），显然，整体比较检验的第一类错误风险将远远高于5％。输出中指明：“Fisher 95％单独置信区间，温度水平间的所有配对比较，同时置信水平＝81.11％”，这就意味着，整体比较检验的第一类错误概率将高达1－81.11％＝18.89％，这样高的第一类错误概率当然是不能容忍的。

Fisher方法也共有三组多重比较的置信区间：

第一组以水平一（温度60）做被减项，其他水平65，70，75时的均值分别减去水平60时的均值得到的置信区间，结果是“65度＞60度”、“70度＞60度”。

第二组以水平二（温度65）做被减项，其他水平70，75时的均值分别减去水平65时的均值得到的置信区间，结果是“75度＜65度”。

第三组以水平三（温度70）做被减项，水平75时的均值减去水平70时的均值得到的置信区间，结果是“75度＜70度”。

在R16新增的对信息进行分组的结果中，其结论与上面的分析相同。

总之，用Fisher方法得到的结论是，在6对均值比较中，有4对差异是显著的；而Tukey方法得到的结论是，在6对均值比较中，只有2对差异是显著的。可见，在要求整体误差率为5％的时候，判定“差异显著”要比简单的两两比较严格得多，而我们当然应该以Tukey方法得到的结论为最终结论：70度显著高于60度及75度；其他组间差异不显著。

5.5.3　多总体等方差检验

在5.5.1节的单因子ANOVA分析基本原理中，我们提到进行单因子ANOVA的三项基本前提，除了数据独立性、正态性假定，最重要的就是等方差性，就是因子在每一水平下所收集到的数据来自方差相等的正态分布。为了考察这项前提是否得到满足，要进行多总体等方差的检验。我们所讨论的一般问题是：

在正态分布的前提下，可以使用Bartlett检验，在正态分布的前提不满足时，可以使用Levene检验，下面结合具体例题加以说明。

例5—17（续例5—15）

考察4种温度，在显著性水平取α＝0.05时，判断温度对烧碱得率是否有显著影响。先检验4组方差是否相等。

选用“数据”与“分组”分别列在两列的存放格式。如果数据是分多列存放的，要先整理数据，使之堆叠而变成采用“数据”与“分组”分别列在两列的存放格式。

选择“统计＞方差分析＞等方差检验（Stat＞ANOVA＞Testfor Equal Variances）”。

在“响应（Response）”栏输入C2列“得率”，“因子（Factors）”栏输入C1列“温度”，如图5—24所示。

图5—24　多总体等方差检验操作图

点击“确定”后，得到如下输出结果及图5—25：

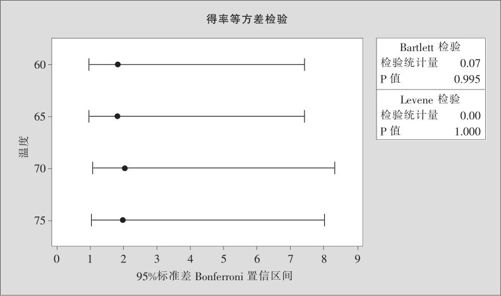
图5—25　多总体等方差检验结果图

结果：ANOVA_单因子.MTW

等方差检验：得率与温度

95％标准差Bonferroni置信区间

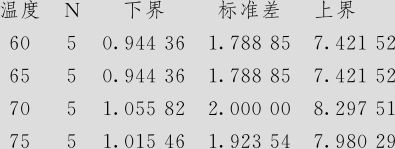
Bartlett检验（正态分布），检验统计量＝0.07，P值＝0.995

Levene检验（任何连续分布），检验统计量＝0.00，P值＝1.000

输出结果的说明如下：

由于假定得率服从正态分布，输出结果选取Bartlett检验，输出的p值＝0.995＞0.05，因此我们的结论是：不能拒绝原假设，即4个温度下得率的方差是相等的。

这里要补充说明的一点是：使用ANOVA是需要三个条件的（详见5.5.1节），即独立、正态、等方差，但在实际应用中，有时样本量较小，直接验证这三个条件几乎没有意义，为此常用残差诊断的方法予以验证，即在图5—21右图中增选“残差图”功能项。详细操作方法及原理请参看9.2.5节回归方程的残差诊断。