4.3　参数的区间估计

设θ是总体的一个待估参数，从总体中获得样本量为n的样本是X₁，X₂，…，X_n，对给定的显著性水平α（0＜α＜1），有统计量：θ_L＝θ_L（X₁，X₂，…，X_n）与θ_U＝θ_U（X₁，X₂，…，X_n），若对任意θ有P（θ_L≤θ≤θ_U）＝1－α，则称随机区间［θ_L，θ_U］是θ的置信水平为1－α的置信区间，θ_L与θ_U分别称为置信下限与置信上限。

置信区间的大小表达了区间估计的精确性，置信水平表达了区间估计的可靠性，1－α是区间估计的可靠程度，而α表达了区间估计的不可靠程度。

如果［θ_L，θ_U］是置信水平为0.95的置信区间，由于随机区间［θ_L，θ_U］会随样本观察值的不同而不同，它有时包含了参数θ，有时没有包含θ，即是说用这种方法作参数的区间估计时，在100次的区间估计中，平均说来，大约有95个区间能包含参数θ，大约有5个区间没能包含θ。

在进行区间估计时，必须同时考虑置信水平与置信区间两个方面。对于置信区间的选取，一定要注意，决不能认为置信水平越大的置信区间就越好。实际上，置信水平定的越大，则置信区间相应也一定越宽，当置信水平太大时，则置信区间会宽得没有实际意义了。这两者要结合在一起考虑，才更为实际。通常我们取置信水平为0.95，极个别情况下可取0.99或0.90，一般不取其他的置信水平。

4.3.1　单正态总体均值的置信区间

当X～N（μ，σ²）时，正态总体均值的置信区间有以下三种情况：

（1）当总体方差σ²已知时，正态总体均值μ的1－α置信区间为：

式中，Z_1－α/2是标准正态分布的1－α/2分位数，也就是双侧α分位数。例如α＝0.05时，Z_0.975为1.96。

在MINITAB中，我们可以通过“统计＞基本统计量＞单样本Z（Stat＞Basic Statistics＞1-Sample Z）”来实现。

由于在实际情况中，已知标准差的情况很罕见，因此我们这里重点关注的是标准差未知时的情形。

（2）当总体方差σ²未知时，σ用其样本标准差S代替，此时正态总体均值μ的1－α置信区间为：

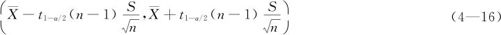
式中，t_1－α/2（n－1）表示自由度为n－1的t分布的1－α/2分位数，也就是t分布的双侧α分位数。例如α＝0.05时，样本量n＝16时，t_0.975（15）＝2.131，其值略大于Z_0.975＝1.96。

例4—4

某集团公司正推行节省运输费用活动，表4—1是某部门20个月使用的运输费用调查结果数据（数据文件：BS_运输费用.MTW）。

表4—1

假设运输费用是服从正态分布的，求运输费用均值的95％置信区间。

解　（1）由于总体标准差未知，选择“统计＞基本统计量＞单样本t（Stat＞Basic Statistics＞1-Samplet）”，在“样本所在列（Samples in columns）”栏中输入数据列，点击“选项（Options）”后，输入置信水平“95”（％），如图4—12所示。

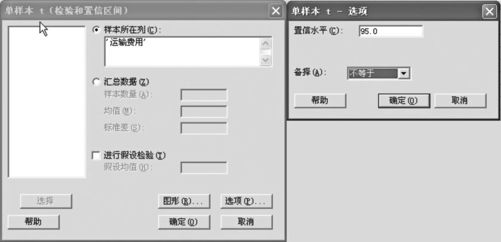
图4—12　单样本t求置信区间操作图

（2）点击“确定”后，得到输出结果如下：

单样本T：运输费用

当全部样本数据给出时，此类问题的计算还可以直接从“统计＞基本统计量＞图形化汇总（Stat＞Basic Statistics＞Graphical Summary）”中得到，在此不再赘述。

（3）前两种情况讨论的是当总体为正态分布时，μ的区间估计，然而当总体不是正态分布时，如果样本量n超过30，则可根据中心极限定理知道：仍近似服从正态分布，因而仍可用正态分布总体时的均值μ的区间估计方法，而且可以直接用样本标准差代替总体标准差，即采用公式：

在MINITAB中，通常直接采用“统计＞基本统计量＞图形化汇总（Stat＞Basic Statistics＞Graphical Summary）”中得到总体均值的置信区间结果。只不过要注意的是：总体非正态时，在小样本情况下此结果并不可信，只有当样本量超过30后，由于中心极限定理的保证，此结果才是可信的。

4.3.2　单正态总体方差和标准差的置信区间

当X～N（μ，σ²）时，正态总体方差的置信区间是：

式中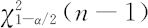，和分别是χ²分布的1－α/2分位数与α/2分位数。

当X～N（μ，σ²）时，正态总体标准差的置信区间是：

例4—5

某集团公司正推行节省运输费用活动，表4—2是某部门20个月使用的运输费用调查结果数据（数据文件：BS_运输费用.MTW）。

表4—2　

假设运输费用服从正态分布，求运输费用方差和标准差的95％置信区间。

解　（1）求总体方差置信区间，选择“统计＞基本统计量＞单方差（Stat＞Basic Statistics＞1 Variance）”。

（2）在“样本所在列（Samples in columns）”栏中输入数据列，点击“选项（Options）”后，输入置信水平“95”（％），如图4—13所示。

图4—13　求单总体方差置信区间操作图

（3）点击“确定”后，得到输出结果如下：

单方差检验和置信区间：运输费用

方法

卡方方法仅适用于正态分布。

Bonett方法适用于任何连续分布。

求总体标准差置信区间另一种方法：选择“统计＞基本统计量＞图形化汇总（Stat＞Basic Statistics＞Graphical Summary）”；在“变量（Variables）”一栏中输入数据列，置信水平输入“95”（％），点击“确定”后，得到输出结果如图4—14和图4—15所示。

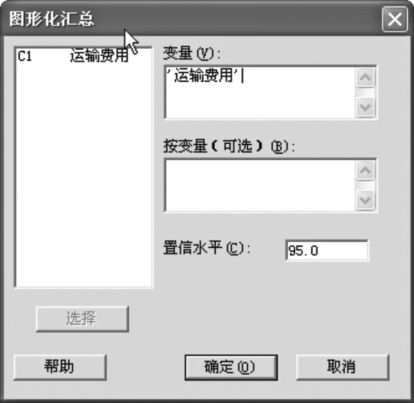
图4—14　求单总体标准差置信区间操作图

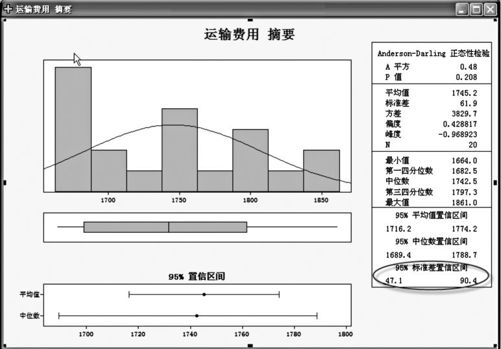
图4—15　单总体标准差置信区间结果图

4.3.3　单总体比率的置信区间

当X～b（1，p）时，也就是X取“非0则1”的0—1分布，我们常需要估计总体中感兴趣的那类比率的置信区间，比如，一批产品中，不合格品率的大致范围；顾客满意度调查中，有抱怨顾客的比率范围等。

这里我们记总体比率为p，样本比率为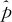。可以证明，当样本量足够大时（要求np＞5及np（1－p）＞5），且p值适中（0.1＜p＜0.9），则可用正态分布去近似二项分布，因而近似有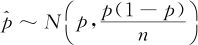：。因此，由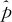服从的正态分布构造总体比率p的置信区间为：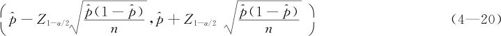

例4—6

某电视台为了调查新节目收视率，在节目放映时间内进行了电话调查。在接受调查的2000名被调查者中有1230名正收看本节目。求此节目收视率的95％置信区间。

解　（1）求总体比率p的置信区间，选择“统计＞基本统计量＞单比率（Stat＞Basic Statistics＞1 Proportion）”，如图4—16所示。

图4—16　求单总体比率置信区间操作路径图

（2）在“汇总数据（Summarized data）”栏中分别输入“2000”、“1230”，点击“选项（Options）”后，输入置信水平“95”（％），如图4—17所示。

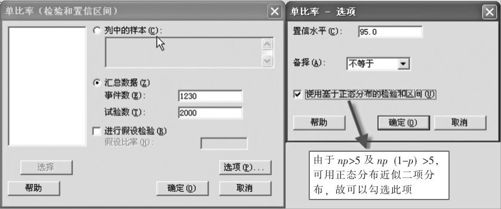
图4—17　求单总体比率置信区间数据输入操作图

（3）点击“确定”后，得到输出结果如下：

单比率检验和置信区间

使用正态近似。

4.3.4　双总体均值差的置信区间

某工厂品质部部长希望了解两家不同原材料供应商提供的原材料强度是否存在差异，这实际上是要对两个总体均值之差做区间估计。

设有两个总体，X～N（μ₁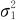，），Y～N（μ₂，），从总体X中抽取的样本X₁，X₂，…，X_n，样本均值为，样本方差为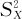，样本标准差为S_X，从总体Y中抽取的样本为Y₁，Y₂，…，Y_m，样本均值为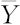，样本方差为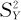，样本标准差为S_Y。

对两总体均值差异μ₁－μ₂的区间估计常有以下三种情况（请读者结合4.1.2节理解）：

（1）两个总体均服从正态分布，且两个总体的方差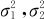都已知时，两总体均值差异μ₁－μ₂的1－α置信水平下的置信区间为：

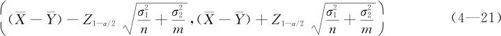
只要样本量足够大，无论两总体的方差是否相等，上述公式都适用。

（2）两个总体均服从正态分布，且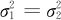，但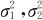均未知时，两总体均值之差μ₁－μ₂的1－α置信水平下的置信区间为：

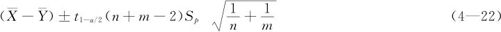
式中，。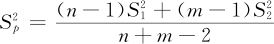

例4—7

一家冶金公司需要减少其排放到废水中的生物氧需求量（biochemical oxygen demand，BOD）含量。用于废水处理的活化泥供应商建议，用纯氧取代空气吹入活化泥以改善BOD（此数值越小越好）。从两种处理的废水中分别抽取10个和9个样品，数据见表4—3（数据文件：BS_生物氧需求量.MTW）。

表4—3　

已知BOD含量服从正态分布，试确定：该公司采用空气和采用纯氧减少BOD含量均值之差的95％置信区间。

解　（1）求两总体μ₁－μ₂的置信区间，选择“统计＞基本统计量＞双样本t（Stat＞Basic Statistics＞2-Samplet）”。

（2）在“样本在不同列中（Samples in different columns）”栏中分别输入C1，C2列，点击“选项（Options）”后，输入置信水平“95”（％），勾选“假定等方差（Assume Equal Variance）”（这里先这样假定，至于对“方差相等”的假定如何进行检验，方法见5.4.2节），如图4—18所示。

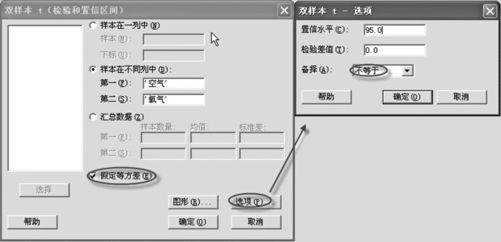
图4—18　求双总体均值差置信区间操作路径图2

3）点击“确定”后，得到输出结果如下：

双样本T检验和置信区间：空气，氧气

空气与氧气的双样本T

差值估计：16.61

差值的95％置信区间：（-0.58，33.80）

差值＝0（与≠）的T检验：T值＝2.04　P值＝0.057　自由度＝17

两者都使用合并标准差＝17.7356

（3）当两个总体均服从正态分布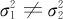，，且方差均未知时，两总体均值之差μ₁－μ₂的1－α置信水平下的置信区间为：

式中，自由度ν的计算公式为：

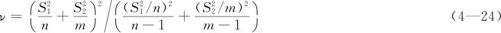
例4—8

假定A，B两名工人生产相同规格的轴棒，关键尺寸是轴棒的直径。由于A使用的是老式车床，B使用的是新式车床，二者精度可能有差异。经检验（检验方法在第5章5.4.2节介绍），他们的直径数据确实来自两个方差不等的正态分布。现他们各测定13根轴棒直径（结果见表4—4，数据文件：BS_轴棒直径.MTW）。

表4—4　

试确定A，B生产的轴棒直径之差的95％置信区间。

解　（1）求两总体μ₁－μ₂的置信区间，选择“统计＞基本统计量＞双样本t（Stat＞Basic Statistics＞2-Samplet）”。

（2）在“样本在不同列中（Samples in different columns）”栏中分别输入C1，C2列，点击“选项（Options）”后，输入置信水平“95”（％），如图4—19所示。

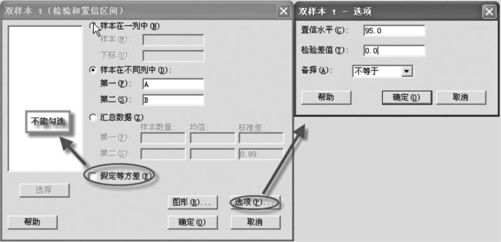
图4—19　求双总体均值差置信区间操作路径图3

（3）点击“确定”后，得到输出结果如下：

双样本T检验和置信区间：A，B

A与B的双样本T

均值

差值估计：1.965

差值的95％置信区间：（0.435，3.496）

差值＝0（与≠）的T检验：T值＝2.71　P值＝0.015　自由度＝17

下面给出一个实例，其中未提供原始数据而只含有摘要数据，计算方法不变。

例4—9

独立随机样本取自均值μ₁，μ₂未知，标准差未知的两个正态分布总体，若第一总体样本标准差S₁＝0.73，样本量n＝25，＝6.9；第二总体样本标准差S₂＝0.89，样本量m＝20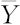，＝6.7。求μ₁－μ₂的95％置信区间。

解　（1）求两总体μ₁－μ₂的置信区间，选择“统计＞基本统计量＞双样本t（Stat＞Basic Statistics＞2-Samplet）”（见图4—20）。

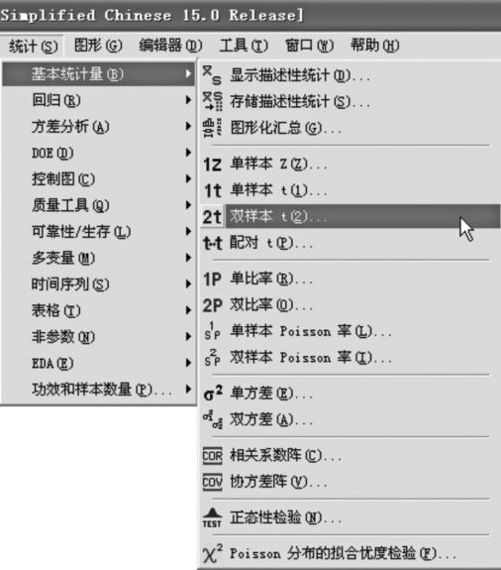
图4—20　求双总体均值差置信区间操作路径图1

（2）在“汇总数据（Summarized data）”栏中分别输入已知样本数据，点击“选项（Options）”后，默认置信水平“95”（％），如图4—21所示：

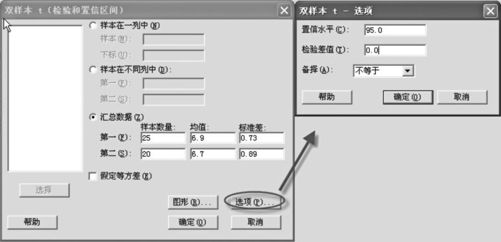
图4—21　求双总体均值差置信区间数据输入操作图

（3）点击“确定”后，得到输出结果如下：

双样本T检验和置信区间

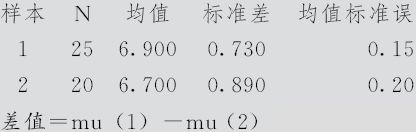
差值估计：0.200

差值的95％置信区间：（-0.301，0.701）

差值＝0（与≠）的T检验：T值＝0.81　P值＝0.423　自由度＝36

对于双总体均值差的置信区间要能理解其含义。以例4—7为例，用纯氧取代空气吹入活化泥后，BOD的样本均值表面上看降低了16.61，但能否根据此数据就断言“纯氧取代空气吹入活化泥后降低BOD的效果显著”呢？这是错误的。我们不能只看样本的均值差，还要看置信区间。我们算出总体均值差的95％置信区间是（-0.58，33.80），换言之，真正的总体的均值差不一定是正数，两总体均值差可能为正，也可能为负。正确的断言应该是目前还“看不出显著降低”。如果置信区间的上限与下限都为正，则可以断言总体均值差为正；如果置信区间的上限与下限都为负，则可以断言总体均值差为负；如果置信区间的上限与下限为一正一负，则目前还不能排除总体均值差为0的可能。此例比较特殊，下限虽然为负，但其绝对值很小，要获得最终结论，要进行更细致的单侧假设检验，关于此问题的结论请参看第5章例5—8的有关讨论。

4.3.5　双总体比率差的置信区间

设两个总体的比率分别为p₁和p₂，为了估计p₁－p₂，分别从两个总体中各随机抽取样本量为n₁和n₂的两个随机样本，并计算两个样本的比率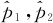，可以证明，p₁－p₂的置信水平为1－α的置信区间为：

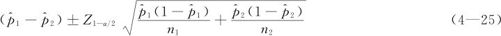
例4—10

为了解员工对工资的满意度，对250名男员工、200名女员工进行调查，结果见表4—5。

表4—5　

求男女员工对工资满意度差异的95％置信区间。

解　（1）求两总体p₁－p₂的置信区间，选择“统计＞基本统计量＞双比率（Stat＞Basic Statistics＞2-Proportions）”。

（2）在“汇总数据（Summarized data）”栏中分别输入数据，点击“选项（Options）”后，输入置信水平“95”（％），勾选“使用p的合并估计值进行检验（Use pooled estimate of pfortest）”，如图4—22所示。

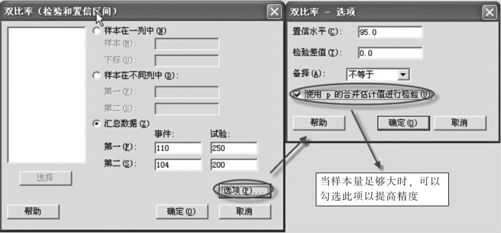
图4—22　双总体比率差置信区间操作图

（3）点击“确定”后，得到输出结果如下：

双比率检验和置信区间

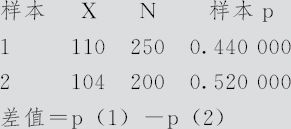
差值估计：-0.08

差值的　95％　置信区间：（-0.172630，0.0126298）

差值＝0（与≠0）的检验：Z＝-1.69　P值＝0.091

Fisher精确检验：P值＝0.106

在本章中，我们介绍了多种置信区间的求法，但并未讲到更多的原理。对于置信区间的理解如果能与假设检验密切联系起来，就会有更深入的体会。等大家学习了第5章所讨论的假设检验问题后，对置信区间的理解就会更加全面。