10.5 变异源分析的一般模型数值方法
变异源分析中会遇到很多不同类型的问题,我们将依次介绍两因子交叉、两因子嵌套、三因子交叉加嵌套等几种类型。由于MINITAB软件只对完全嵌套因子的模型给出直接结果,我们对于一般模型只好采用一般线性模型方法。我们先对此进行一些介绍,然后再用各自的例子具体说明。
10.5.1 一般线性模型的方差分量计算
在实际工作中所遇到的问题,因子的个数可能是2个、3个或更多个;这些因子间的关系可能是交叉关系,可能是嵌套关系,多因子时更可能先交叉后嵌套,或先嵌套后交叉,也可能交叉到底,也可能嵌套到底;因子的效应可能是固定效应,也可能是随机效应;各因子搭配时所使用的水平数一般是固定的,但也不免有个别缺失水平的(如试验失败、记录短缺等);情况千差万别。只是由于在变异源分析中常常会遇到多个因子都是随机效应,而且因子间的关系是嵌套到底的,因此MINITAB软件对此专门开设了窗口,只处理此种模型,这给我们带来很大的方便。但我们必须学会处理一般的情况以应对不同类型的问题。
MINITAB软件在ANOVA类型下,提供了两个具有一般功能的窗口:平衡方差分析(Balanced ANOVA)及一般线性模型(General Linear Model)。其实二者功能相差不多,而平衡方差分析也只是要求所有观测值是平衡的,也就是说,每个因子所取的水平数在整个数据集中都保持不变。由于一般线性模型应用更广泛些,因此在本部分中只介绍一般线性模型方法,平衡方差分析与此几乎完全相同,读者可以自行学习使用。我们对此模型只进行一般介绍,具体使用可以参见后面的例题。
一般线性模型适用于多种情况,在使用时有下列三个步骤(详见例10—5):
第一步,要学会如何“建立模型”。其实很简单,基本规则是:如果因子B被因子A所嵌套,则除了考虑因子A的方差分量外,还要考虑B的方差分量,这项用B(A)表示;如果因子B与因子A是交叉关系,则除了考虑两个因子A,B自身方差分量外,还要考虑二者交互效应的方差分量,此项用A*B表示。举例如下:
(1)考虑二因子交叉模型,则模型可写成:
Y=A+B+A*B+error
而在实际填写时,“error”是所有模型所共用的,故省略不写;另外,MINITAB软件规定,用“空格”连接的并列两项默认为相加。因此,上述模型实际上可以写为:
Y=A B A*B
为了印刷上不被误解,本节中仍保留“+”号。
两交叉因子模型也可简写为:
Y=A|B
(2)考虑二因子嵌套模型,B被A所嵌套,则模型可写成:
Y=A+B(A)
(3)考虑三因子嵌套模型,B被A所嵌套,C被A,B所嵌套,则模型可写成:
Y=A+B(A)+C(AB)
(4)考虑三因子模型全交叉,则模型可写成:
Y=A+B+C+AB+AC+BC+AB*C=A|B|C
(5)考虑三因子模型,A,B交叉,C被A,B所嵌套,则模型可写成:
Y=A+B+A*B+C(AB)=A|B+C(AB)
(6)考虑三因子模型,B被A所嵌套,C与A,B交叉,则模型可写成:
Y=A+B(A)+C+AC+BC
更多的因子情况与此类似,在此不再赘述。
第二步,选定随机效应项。由于在一般线性模型中,默认的是固定效应,因此如果某因子是随机效应则应该将此因子列入“随机效应因子”的表格中。要注意的是,在SOV中,除极个别情况外,所有的因子都是随机效应因子,计算中不要漏选此项。对于固定效应项,各因子效应是固定常数,根本没有方差分量可言。
第三步,增选输出“方差分量结果”。由于在一般线性模型中,默认的是固定效应,没必要计算方差分量,因此在进行SOV时,必须在操作中注意,在填写完“响应变量”名称、“模型”内容、“随机因子”名称后,打开“结果(Result)”窗,勾选“显示期望均方及方差分量(Display Mean Square and Variance Component)”。具体操作的图形界面可以参见图10—11和图10—12,那里有使用一般线性模型计算方差分量的操作图。
在一般线性模型的方差分量计算中,由于情况的不同导致具体方法与公式也很不相同。下面给出有双因子交叉、双因子嵌套及三因子先交叉后嵌套共三种常见类型的例题,其他情况就不再叙述了。
10.5.2 双因子交叉型方差分量计算
我们先回顾一下例10—2中的问题。
例10—5(续例10—2)
在生产精密轴杆过程中,随机选取3个工人,都使用相同的4台车床,各自加工出3根轴杆,其数据列于表10—2中。由于因子A(工人)中每个水平与因子B(车床)各水平(各车床)都进行了全面搭配,显然A与B是交叉的。
对于两个交叉因子计算其方差分量。
解 设Yijk为在因子Ai水平和因子Bj水平搭配下,所得到的第k个观测值。将Ai水平的随机效应记为αi,因子Bj的随机效应记为βj,因子Ai水平和因子Bj水平的随机交互效应记为δij,记εijk为随机误差,则可以有下列模型:
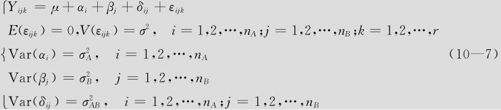
式中,随机误差εijk与αi,βj及δij之间都不相关。此模型中的 及σ2都是方差分量,模型(10—7)也称为交叉二因子方差分量模型。
及σ2都是方差分量,模型(10—7)也称为交叉二因子方差分量模型。
可以证明有下列公式(参见参考文献[15]蒙哥马利:《实验设计与分析》,246页):

式中,各项MS是在ANOVA表中的均方,对这些均方的期望值用对应的均方的观测值来估计,可得到相应方程组,解这些方程组就可以得到方差分量的估计结果:

对于例10—2,下面给出一个完整的步骤介绍。为此,先画出多变异图,然后给出方差分量的计算结果。
由于有交叉关系的两个因子间可以交换顺序,哪个在上面都无所谓,可以把因子B(车床)作为最高层,结果如图10—10所示(画多变异图的方法可以参看10.3节)。
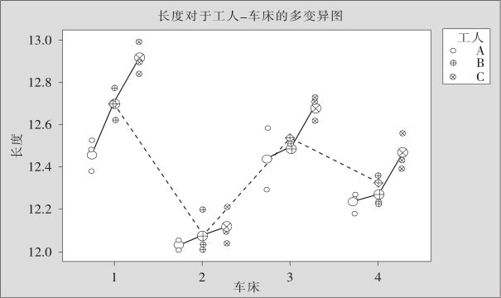
图10—10 轴杆长度多变异图
从上图可以看出车床间有明显变异,工人间似乎也有些变异,几根轴杆间随机波动也有些。究竟各项方差中大小的顺序如何、各占多大比率等问题则要经过下面的数值计算。使用一般线性模型计算方差分量的操作如图10—11及图10—12所示。
从“统计>方差分析>一般线性模型(Stat>ANOVA>General Linear Model)”入口(见图10—11,打开窗口后的操作见图10—12)。
在“响应(Response)”中填写“‘长度’”;在“模型(Model)”中填写“‘车床’‘工人’‘车床’*‘工人’”;在“随机因子”内填写“‘车床’‘工人’”;打开“结果(Results)”后,勾选“显示期望均方和方差分量(Display Mean Square and Variance Component)”,则可以得到最后结果:
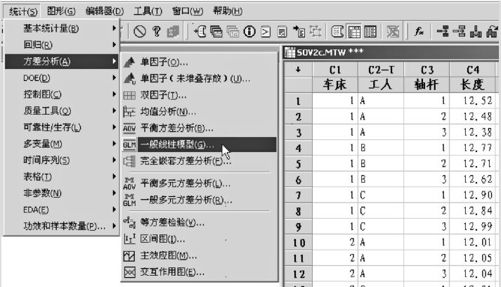
图10—11 使用一般线性模型计算方差分量操作图
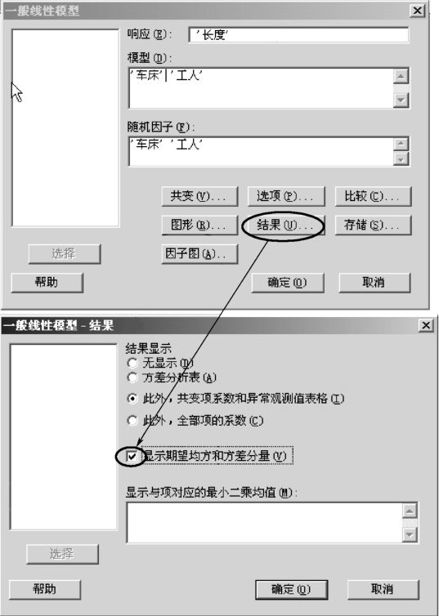
图10—12 使用一般线性模型的模型输入图
计算结果中的最后一部分如下:
期望均方,使用调整的SS
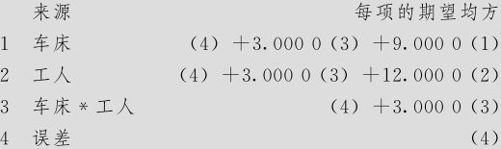
检验的误差项,使用调整的SS
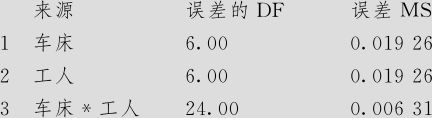
方差分量,使用调整的SS

上面计算结果中,只有方框中最后一段内容是我们所需要的,这里列出了各项方差分量的估计值。据此结果可以画出方差分量的Pareto图(见图10—13)。
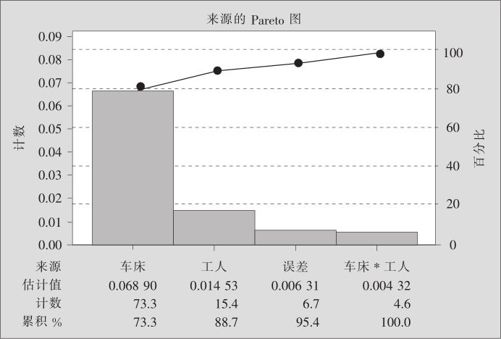
图10—13 轴杆生产过程方差分量Pareto图
本例中,车床的方差分量所占比率最大(达73.3%),工人间方差分量所占比率较小(只有15.4%)。这样一来,为了解决轴杆长度的波动过大问题,必须先从“车床间的差异为何这么大”开始分析,而且要设法将其尽可能缩小。获得这样的结论就是我们使用SOV的主要成果。
10.5.3 双因子嵌套型方差分量计算
例10—6(续例10—1)
我们先回顾一下例10—1中的双因子嵌套问题。
考虑螺钉直径波动过大问题。随机选取3名工人,让他们都使用自己平时所用的车床,按随机顺序各自分别加工出4颗螺钉,然后在每颗螺钉的根部随机选取两个相互垂直的方向,分别测量其直径,共得到24个数据。我们要分析螺钉直径间的变异产生的原因。由于因子B(螺钉)的各水平是由因子A(工人)所决定的,因此,因子B是被因子A所嵌套的。
对于两个嵌套因子计算其方差分量。
解 设Yijk为在因子Ai水平和因子Bj水平搭配下,所得到的第k个观测值。将因子Ai水平的随机效应记为αi,因子Bj水平的随机效应记为βj,随机误差效应记为ε(ij)k,则可以有下列模型:
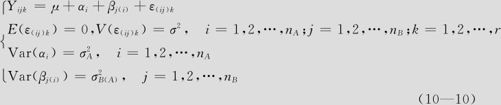
式中,随机误差ε(ij)k与αi及βj(i)之间都不相关。此模型中的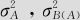 及σ2都是方差分量,模型(10—10)被称为嵌套二因子方差分量模型。
及σ2都是方差分量,模型(10—10)被称为嵌套二因子方差分量模型。
可以证明有下列公式(参见附录参考文献[15]蒙哥马利:《实验设计与分析》,503页):

式中,各项MS是ANOVA表中的均方,对这些均方的期望值用对应的均方的观测值估计,可得到相应方程组,解这些方程组就可以得到方差分量的估计结果:

对于例10—1,我们已先画出了多变异图(见图10—4),下面用两种方法给出方差分量的计算结果。
由于在MINITAB软件中,对于ANOVA完全嵌套模型给出专门的窗口,因此可以直接进入此窗口得出详细结果。从“统计>方差分析>完全嵌套方差分析(Stat-ANOVA-Fully Nested ANOVA)”入口,操作如图10—14所示。
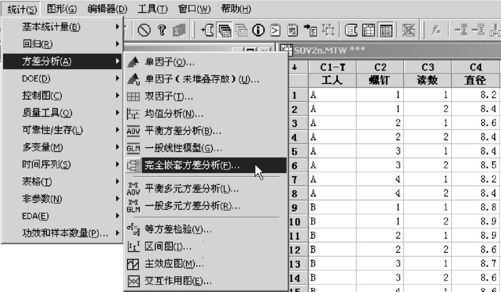
图10—14 ANOVA完全嵌套模型的方差分量计算操作(1)
打开窗口后的操作见图10—15。在“响应(Response)”中填写“‘直径’”;在“因子(Factor)”中依次填写“‘工人’‘螺钉’”。请注意:填写因子的顺序时一定要将树状图中的因子排列按由上到下的顺序输入,本例题一定要先写“工人”,再写“螺钉”。
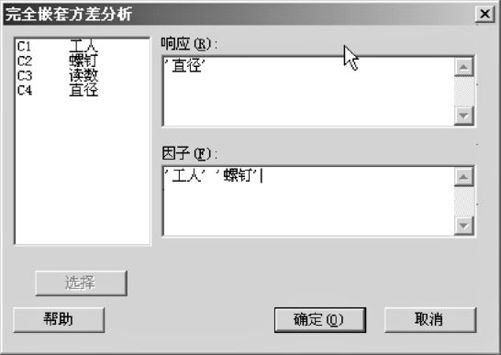
图10—15 ANOVA完全嵌套模型的方差分量计算操作(2)
计算结果如下:
对于直径的方差分析

方差分量
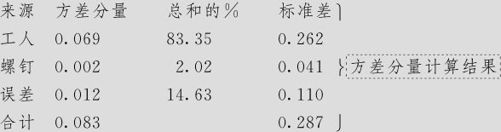
期望均方
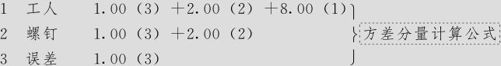
上述结果比较完整,不但给出方差分量计算结果,而且给出各分量的贡献率,还给出标准差结果。
对于本例,同样可以用一般线性模型得到结果。其模型应该是这样的:
Y=A+B(A)
从“统计>方差分析>一般线性模型(Stat>ANOVA>General Linear Model)”入口,打开窗口后的操作见图10—16。在“响应(Response)”中填写“‘直径’”;在“模型(Model)”中填写“‘工人’‘螺钉’(‘工人’)”;在“随机因子”内填写“‘工人’‘螺钉’”;打开“结果(Results)”后,在“显示期望均方和方差分量(Display Mean Square and Variance Component)”项前勾选之,则可以得到最后结果。
其计算结果如下:
方差分量,使用调整的SS

这里只有方差分量结果。Pareto分析结果如图10—17所示(画Pareto图的方法可以参看10.4.4节中在例10—4中介绍过的内容)。
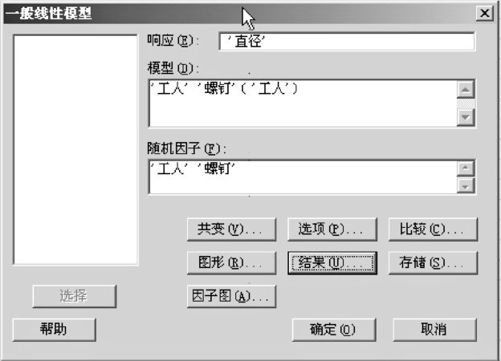
图10—16 ANOVA一般线性模型交叉二因子的方差分量计算
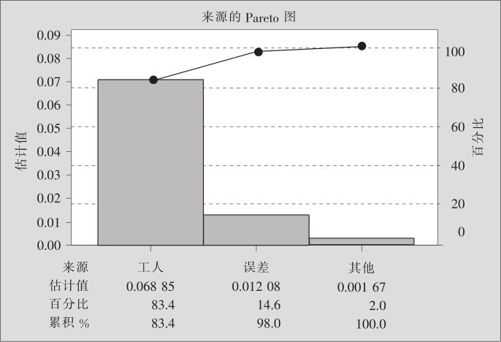
图10—17 嵌套二因子的方差分量Pareto图
这里要提醒大家注意,从例10—1中的多变异图(见图10—4)中,很容易看出工人间的差异非常显著;从方差分量的计算中也证实了这一点,“工人”的方差占总方差量达到83.4%。似乎多变异图已经基本上抓住了方差分量的结构,方差分量的计算似乎可有可无。实际上这种概念是错误的,这是因为多变异图只展现了表面现象,很容易出现“视觉误差”。下面再举一例,也是双因子嵌套结构的,但多变异图展现的表面现象所造成的直观感觉并不一定对。
例10—7
焊锡膏涂抹量问题。为了研究焊锡膏涂抹机在涂抹焊锡膏过程中波动过大的原因,使用了3批焊锡膏,每批焊锡膏各随机挑选了4管焊锡膏,对每管焊锡膏都涂抹在3个不同的点上。烘烤后,将焊锡膏刮掉,测量其涂抹量(单位:毫克)。全部数据记录在表10—5中(数据文件:QT_SOV焊锡膏.MTW)。
表10—5 焊锡膏涂抹量数据表

用多变异图可以看出焊锡膏涂抹量的变化状况(见图10—18)。
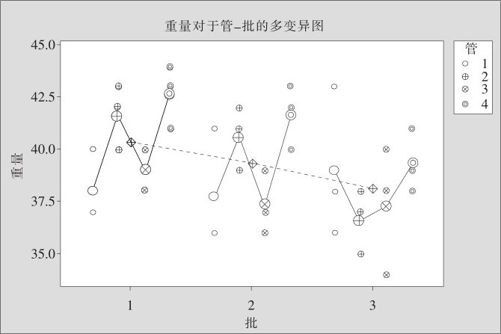
图10—18 焊锡膏涂抹量的多变异图
从上图中可以得到什么信息呢?对于变异状况,可以看出3个“批”之间差异很小,而“管”之间的差异比较大,同一“管”内的3个点之间也有差异。那么究竟是“管”间差异更大还是“点”间差异更大?从图上看,似乎“管”间差异更大些,波动更严重。但应该想到,即使“管”之间没有波动,但由于“管”的均值是由“点”的值平均而来的,“点”间波动必然会导致“管”间均值的波动,要想计算出“管”之间的真正波动量(方差分量),必须将“管”间波动扣除掉“点”波动造成的影响才行,这就是我们要计算“方差分量”的意义所在。
从“统计>方差分析>完全嵌套方差分析(Stat>ANOVA>Fully Nested ANOVA)”入口,打开窗口后,在“响应(Response)”中填写“‘焊膏量’”;在“因子(Factor)”中依次填写“‘批’ ‘管’”,计算结果如下:
嵌套ANOVA:重量与批,管
对于重量的方差分析

方差分量
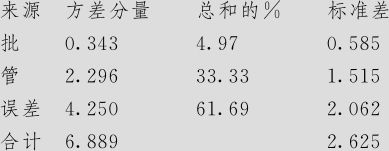
期望均方

可以看出,误差的方差分量为4.250,占总方差的61.69%;“管”之间的方差分量为2.296,占总方差的33.33%;可见随机误差项才是产生波动的真正的“罪魁祸首”。但是在实际工作中,得到这样的结果是失败的,因为这表明“随机误差”中含有值得更细致考虑的因子,需要将误差项继续细分,否则无法指明改进方向。
画出方差分量的Pareto图(见图10—19),可以得到更直观的结论。
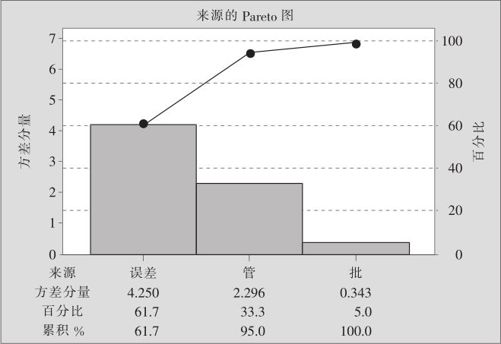
图10—19 焊锡膏涂抹量方差分量的Pareto图
10.5.4 三因子方差分量计算
例10—8(续例10—3)
下面讨论例10—3轴棒直径变异问题(三因子)。3名工人A,B及C,让他们使用已选好并编了号的固定的4台车床,各自分别加工出3根轴棒,然后在每根轴棒的根部测出两个相互垂直方向的直径。这里考虑了工人、车床及轴棒共三个因子。计算各项方差分量。
解 下面先画出多变异图(见图10—20)。
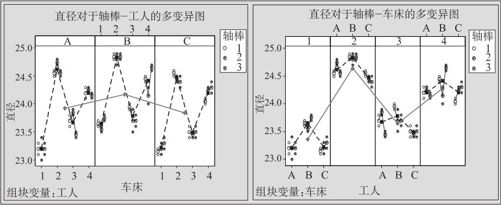
图10—20 轴棒生产三因子的多变异图
从图10—20左可以看出,车床间差异显著,工人间差异有一些,轴棒间差异也有一点。将“车床”与“工人”两因子颠倒后画出的多变异图将更清楚地显示这一结果(见图10—20右)。到底每项各占多大比率?这要经过方差分量的计算。
容易看出,工人与车床间是交叉关系,而轴棒被二者所嵌套,所以写出模型应该是:
Y=A+B+A*B+C(AB)
从“统计>方差分析>一般线性模型(Stat>ANOVA>General Linear Model)”入口,打开窗口后的操作见见图10—21。在“响应(Response)”中填写“‘直径’”;在“模型(Model)”中依次填写“‘工人’|‘车床’‘轴棒’(‘工人’‘车床’)”;在“随机因子”内填写“‘工人’‘车床’‘轴棒’”;打开“结果”后,在“显示期望均方和方差分量”项前勾选之,则可以得到最后结果:
期望均方,使用调整的SS

检验的误差项,使用调整的SS
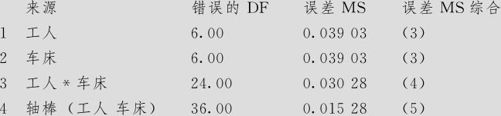
方差分量,使用调整的SS
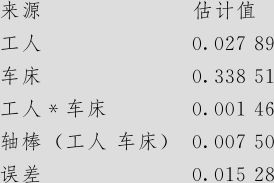
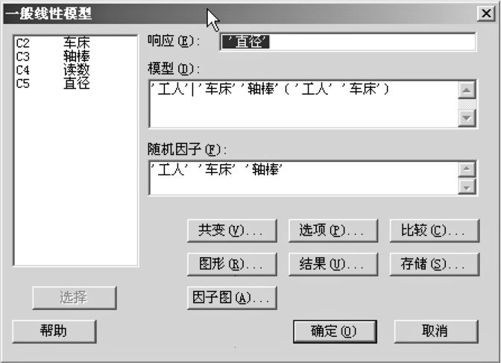
图10—21 轴棒三因子的方差分量计算
上述输出结果中后一个部分是最终计算出的方差分量结果。画出Pareto图如图10—22所示。
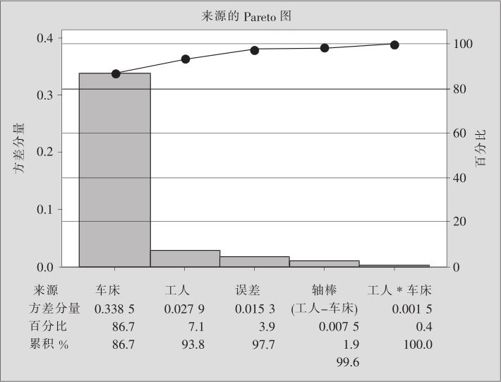
图10—22 轴棒三因子的方差分量Pareto图
从图10—22中明显看出,车床间的方差分量贡献最大,竟达到86.7%。工人之间也有差别,但相比于车床间的差别小多了(只占7.1%)。这说明,轴棒直径间的差异主要是由不同的车床间差异造成的。这可以从图形中直观分析看出,但方差分量的计算给出了定量的分析结论。
实际问题可能千差万别,但变异源的分析方法大同小异。我们主要应该一方面掌握多变异图的图形分析方法,得到一个粗略的结论,另一方面掌握完全嵌套方差分量计算方法及有更广泛应用的一般线性模型方差分量计算方法,使一般问题都可以得到解决。
