6.4 单双总体Poisson率检验
从6.1节到6.3节,我们讨论的都是离散变量为二项分布的情形。如果离散变量服从Poisson分布,如何进行分布的拟合优度检验以及参数的估计和检验呢?
在MINITABR15以前的版本中,没有专门的窗口处理这类问题,自MINITABR15开始增加了Poisson分布的拟合优度检验方法(参见6.3.3.1节),也增加了单Poisson分布总体的Poisson率(即Poisson分布的均值)检验,及双Poisson分布总体的Poisson率相等性检验。这里将在6.4.1节及6.4.2节中分别介绍单、双Poisson分布总体的Poisson率检验。
6.4.1 单总体Poisson率检验
Poisson分布总体的Poisson率其实就是其分布的均值,因此本段相应于正态分布的单总体均值检验。先看一个例题。
例6—14
某芯片生产流水线生产8英寸片,每小时抽取3片,检测总共有多少个瑕疵点。根据一般见解,我们可以假定瑕疵点个数是服从Poisson分布的(也通过了分布的检验)。在六西格玛团队改革生产前,平均瑕疵点数为8。对于改革后的状况,共收集了26个小时的数据,列在表6—21中(数据文件“BS_瑕疵点比较.MTW”中第2列“改革后”,见图6—20)。
表6—21

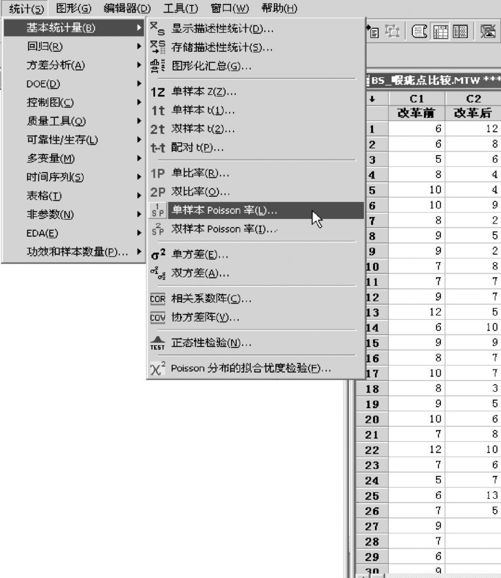
图6—20 单总体Poisson率检验操作1
问:改革后平均瑕疵点数确实下降了吗?
解 本问题要检验的假设是:
H0:λ=8
H1:λ<8
MINITAB软件给出了两种方法进行检验的计算。样本量较小时,用精确方法计算;当样本增大后,使用正态近似算法。一般都用精确算法。
依次选择“统计>基本统计量>单样本Poisson率检验(Stat>Basic Statistics>1Sample Poisson Rate)”(见图6—20)。
可以见到如图6—21所示界面。
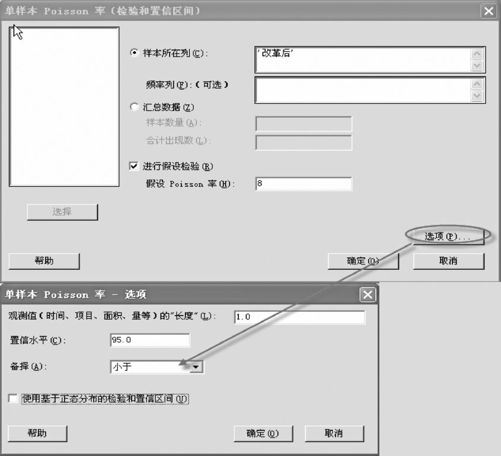
图6—21 单总体Poisson率检验操作2
一般情况下,在图6—21下半部的“观测值的长度”项通常都取为1。对于其下方“使用基于正态分布的检验和置信区间”的选项,如果不勾选,则表示只进行精确计算;如果勾选,则表示还要进行正态近似的计算。一般我们是不勾选的。MINITAB计算后可以得到下列结果:
单样本Poisson率:改革后的检验和置信区间
比率检验=8与比率<8

观测值的“长度”=1
计算结果表明:在26次检验(每次3片芯片)中,总共发现瑕疵点数175个,因此平均瑕疵点数(出现率)为6.73个。以95%的把握可以断言,平均瑕疵点数肯定小于7.6,也就肯定小于8,而检验的精确p值为0.011<0.05,因此应该拒绝原假设,也就是说,可以断言平均瑕疵点数肯定比8小,即平均瑕疵点数确实有所降低。
例6—15(续例6—10)
每天检查10000支二极管,其结果按出现不合格二极管的天数整理成表6—18(数据文件:TBL_二极管不合格数.MTW),平均不合格二极管的支数可以认为是2吗?
解 本问题要检验的假设是:
H0:λ=2
H1:λ≠2
由于此数据是整理过的带有观测频数的数据,因此输入格式稍有差别。图6—20中的上半部应该增加频率列,如图6—22所示。
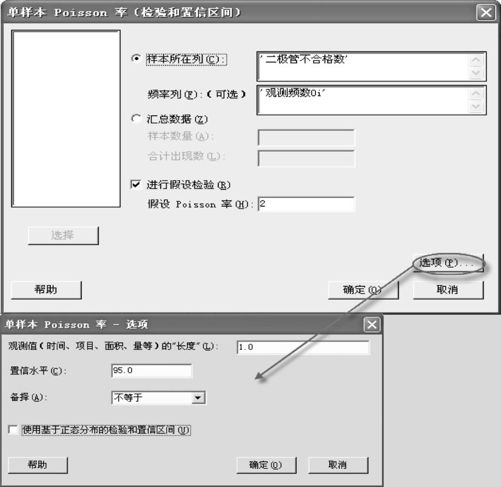
图6—22 单总体Poisson率检验操作3
当然也要注意把“选项”中的备择假设设定为“不等于”。计算结果如下:
单样本Poisson率:二极管不合格数的检验和置信区间
使用频率与观测频数
比率检验=2与比率≠2

观测值的“长度”=1
输出结果说明:由于p值=0.944>0.05,故不能拒绝原假设,即平均不合格二极管的支数可以认为是2。
这里还要特别说明的是,使用单总体Poisson率检验需要什么条件呢?与单总体正态分布均值检验的条件相似,这里也有两个要求:(1)观测数据相互独立;(2)分布服从Poisson分布。如何进行这两项的检验不再赘述,独立性的检验在离散型及连续型两种类型间检验方法相同(因为游程检验法是非参数检验法,对分布无任何特别要求);服从Poisson分布的检验已在6.3.3.1节讲述。
6.4.2 双总体Poisson率检验
Poisson分布总体的Poisson率其实就是其分布的均值,因此本部分相应于正态分布的双总体均值相等性检验。先看一个例题。
例6—16
假定瑕疵点个数服从Poisson分布,在六西格玛团队改革生产前后,分别收集了30个小时和26个小时的数据,列在表6—22和表6—23中(数据文件:BS_瑕疵点比较.MTW)。
改革生产前:
表6—22

改革生产后:
表6—23

问:改革生产后的平均瑕疵点个数比改革生产前确有降低吗?
解 记改革生产前平均瑕疵点个数为λ1,改革生产后的平均瑕疵点个数为λ2。
本问题要检验的假设是:
H0:λ1=λ2
H1:λ1>λ2
或改写为:
H0:λ1-λ2=0
H1:λ1-λ2>0
MINITAB软件给出了两种方法进行检验的计算。样本量较小时,用精确方法计算;当样本增大后,使用正态近似算法。一般用精确算法。
从“统计>基本统计量>双样本Poisson率检验(Stat>Basic Statistics>2-Sample Poisson Rate)”入口,可以见到如图6—23所示界面。
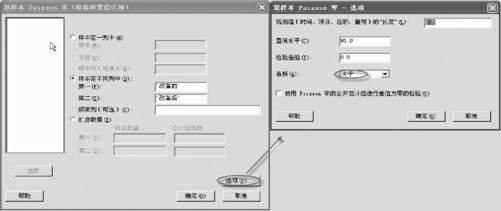
图6—23 双总体Poisson率检验操作1
注意在“选项”中的备择假设设定为“大于”,则可以得到下列结果:
双样本Poisson率:改革前、改革后的检验和置信区间

差值估计:1.30256
差值的95%置信下限:0.108879
差值=0(与>0)的检验:Z=1.79 P值=0.036
精确检验:P值=0.041
计算结果表明:在改革前的30次检验(每次3片芯片)中,总共发现瑕疵点数241个,因此平均瑕疵点数(出现率)为8.03个。在改革后的26次检验(每次3片芯片)中,总共发现瑕疵点数175个,因此平均瑕疵点数(出现率)为6.73个。二者的样本平均瑕疵点数差为1.30个,以95%的把握可以断言,平均瑕疵点数差即肯定大于0.109,即肯定大于0。而检验的精确p值为0.041<0.05,因此应该拒绝原假设。也就是说,可以断言平均瑕疵点数差肯定为正值,即改革后平均瑕疵点数确实比改革前有所降低。
使用双总体Poisson率检验需要什么条件呢?与单总体Poisson率检验需要的条件完全相同。这里也是两个要求:(1)各总体观测数据相互独立;(2)两总体分布都服从Poisson分布。原来双正态总体的均值相等性检验中,要求“两总体方差相等”,现在与之相应的这一条在这里被取消了,因为这里进行的是精确检验,p值是未使用任何统计量分布而直接计算出来的,因此不必增加附加条件。
