13.1　试验设计基础

13.1.1　试验设计中的基本术语

一般实际问题都是复杂的，任何数学模型都只是它的某种抽象概括。试验设计也不例外。我们先给出一些有关试验设计的简单基本概念的描述，稍后将给出一些更深入的概念的定义。

1．因子：可控因子与非可控因子

将过程模型简化为图13—1，其中y₁，y₂，…，y_s是我们关心的s个输出变量，这些常被称为“响应变量”（response）或“指标”。当然在一般情况下，应该同时考虑多方面指标，可是这太复杂了，我们将在13.5节简单叙述解决此类多指标问题的一些方法。除此之外，在本章的试验设计中，将只考虑单个响应变量的情况。

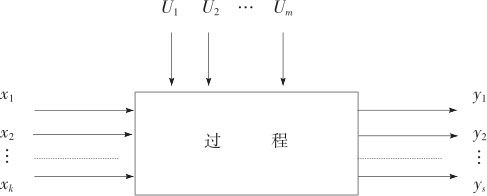
图13—1　过程模型示意图

我们将影响响应变量的那些变量称为试验问题中的“因子”（factor）。我们假定，x₁，x₂，…，x_k是人们在试验中可以加以控制的因子（称“可控因子”），（controlled factor），它们是输入变量，是影响过程最终结果的。这些变量可以是连续型的（通常是这样），也可以是离散型的。影响过程及结果的变量除了这些可控因子还可能包含一些可以记录但不可控制的“非可控因子”（uncontrolled factor）：U₁，U₂，…，U_m，它们通常包括环境状况、操作员、材料批次等。这些变量可能取连续值，也可能取离散值。对于这些变量，通常很难将它们控制在某个精确值上，实际问题中它们确实也可能取不同的值。我们也把这些非可控因子称为“噪声因子”（noise factor），常把它们当作试验误差来处理。

2．水平及处理

为了研究因子对响应的影响，需要用到因子的两个或更多个不同的取值，这些取值称为因子的“水平”（level）或“设置”（setting）。各因子皆选定了各自的水平后，其组合称为“处理”（treatment）。一个处理的含义是，各因子按照设定的水平的一个组合，按此组合我们能够进行试验并获得响应变量的观测值（当然也可以进行多次试验）。因此处理也可以代表一种“安排”，它比“试验”（trail或experimental run）或“运行”（run）含义更广泛些（因为一个处理可以进行多次试验）。

3．试验单元与试验环境

指对象、材料或制品等载体，处理（即试验）应用其上的最小单位称为“试验单元”（experiment unit）。例如，按因子组合规定的工艺条件所生产的一件（或一批）产品，接受治疗的一个病人等。

以已知或未知的方式影响试验结果的周围条件，称为“试验环境”（experiment environment）。这里通常包括温度、湿度、电压等非可控因子。

4．模型与误差

考虑到影响响应变量y的可控因子是x₁，x₂，…，x_k。因此，在试验设计中建立的数学模型是：

式中，y是响应变量；x₁，x₂，…，x_k都是可控因子；f是某个确定的函数关系。式中的误差ε除了包含由非可控因子（或噪声）所造成的“试验误差”（experimental error）外，还可能包含“失拟误差”（lack of fit）。这里，失拟误差是指我们所采用的模型函数f与真实函数间的差异。试验误差与失拟误差这两种误差性质是不同的，分析时也要分别处理。有时为了简化，常假定函数关系f是准确的，从而可以忽略失拟误差。从上述概念中还可以看到，试验误差本身也包含了测量误差。为了不使测量误差影响分析结果，通常要在试验进行前，先进行测量系统的分析，只有测量误差满足了对测量系统的最低要求后，试验才能开始进行。有关测量系统的分析在第11章中已作了细致的讨论。本章介绍的分析方法都假定测量系统已经通过了合格评估，因此不再考虑测量误差。

建立模型（13—1）的重要目的是希望找到使响应变量y达到最优的条件。所谓“最优”，在实际工作中常常有三种不同特性要求：一种是希望y越大越好，称之为“望大”；另一种是希望y越小越好，称之为“望小”；第三种是希望y与某个目标值越接近越好，称之为“望目”。当然，对于望目型问题，设一个新的响应变量，它的值是y与目标值差的绝对值或差的平方，则这样就可以将“望目”型问题转化为“望小”型问题。对于不同特性要求的响应变量，在选取试验设计方法时是有区别的，详细内容会在有关部分再予以讨论。

5．主效应和交互效应

关于各因子的效应以及两因子间的交互作用概念，已在第10章作了介绍。那里指出“效应”分为固定效应和随机效应，而实际工作中，除了变异源分析外，通常只讨论固定效应，这时对于效应的估计要由样本观测值得出，例如用样本均值估计总体的均值等，以下为叙述简洁，我们将“效应的估计量”简称为“效应”。我们在本章要更细致地将它们精确化、定量化。下面举一个最简单的因子设计来说明主效应和交互效应的概念及计算。

例13—1

在合成氨生产中，考虑两个因子，每个因子皆2水平。A：温度，低水平：700摄氏度；高水平：720摄氏度。B：压力，低水平：1200帕；高水平：1250帕。以产量Y为响应变量（单位：kg），列表如下（见表13—1）：

表13—1　可加模型数据表

如何分析因子A温度的效应呢？由于A处于低水平的情况（不考虑因子B），得到的产量的平均值是（200＋230）/2＝215kg，A处于高水平的情况（不考虑因子B），得到的产量的平均值是（220＋250）/2＝235kg。产量由215kg提高到235kg完全是因子A的作用。这时，称因子A的“主效应”（main effect）为235－215＝20kg。

同样可以算出：

因子B的主效应＝［（230＋250）/2－（200＋220）/2］＝240－210＝30（kg）

不但如此，我们还发现，当B（压力）处于高水平时，因子A的效应为250－230＝20，当B（压力）处于低水平时，因子A的效应仍然为220－200＝20，二者完全相同。如果以因子A为横轴，以响应变量（产量）为纵轴作图（见图13—2），可以看出，两条线是平行的。

图13—2　无交互作用时的效应图

如果数据换成另一组，见表13—2：

表13—2　有交互作用的数据表

由于A处于低水平的情况的产量的平均值是（200＋230）/2＝215kg，A处于高水平的情况得到的产量的平均值是（220＋270）/2＝245kg。我们称因子A的主效应为245－215＝30kg。同样可以算出：

因子B的主效应＝［（230＋270）/2－（200＋220）/2］＝250－210＝40（kg）

我们发现，当B（压力）处于高水平时，因子A的效应为270－230＝40，当B（压力）处于低水平时，因子A的效应为220－200＝20，二者大不相同。仍以因子A为横轴，以响应变量（产量）为纵轴作图（见图13—3），可以看出，两条线是不平行的。

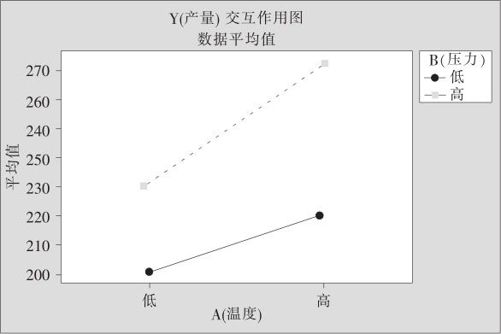
图13—3　有交互作用时的效应图

定义两因子间的交互作用为：如果因子A的效应依赖于因子B所处的水平时，则称A与B之间有交互作用（interaction）。

显然，在前组数据（见表13—1）中，因子A与因子B没有交互作用。在后组数据（见表13—2）中，因子A与因子B是有交互作用的。那么，如何度量交互作用的大小呢？如果没有交互作用，当因子B处于不同水平时，因子A的效应是固定不变的，因此我们要考虑的定义交互效应的出发点就是，当因子B处于不同水平时，因子A的效应到底差了多少？因此，定义交互效应（interaction effect）为下式：

在后组数据中，交互效应A*B＝［（270－230）－（220－200）］/2＝10。同样，交换AB顺序，可以得到公式：

交互效应BA＝［（270－220）－（230－200）］/2＝10，显然二者是相同的。以后，我们不再区分AB或B*A。仔细分析式（13—3）与式（13—4）可以看出，在上述计算公式中，其实是两项同水平（皆高水平，或皆低水平）之和与两项不同水平（一高水平一低水平）之和的差值之半，也就是说，还可以得到计算交互效应的另一个变形的公式：

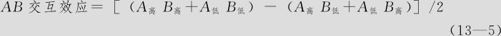
用本例数据代入，即得交互效应

A*B＝［（270＋200）－（230＋220）］/2＝10

式（13—5）可以帮助我们理解在后面讲到的从正交表中直接分析交互效应的计算公式。

要注意的是，如果两个因子间存在显著的交互作用时，应该将主效应和交互效应结合在一起考虑，而不能只用主效应大小作为该因子是否重要的判断依据。有时一个因子主效应很小，但只要某个含它的交互效应显著，则这个因子就是重要的，就得予以保留。

试验设计的内容中，有很大一部分是讨论因子的效应的，上述有关主效应及交互效应的概念是非常重要的。

13.1.2　试验设计的基本原则

有三个基本原则在试验设计中必须要考虑：完全重复（replication）、随机化（randomization）和区组化（blocking）。这些原则早在20世纪20年代，就由伟大的统计学家费雪（R. A. Fisher）首先提出。当时，他在英国的Rothamsted农业试验站工作，由于农业试验规模较大，花费时间长，而且必须妥善处理田间差异等问题，他提出的这些原则获得了巨大的成功。这些原则直到现在仍然有重要的指导意义。

所谓完全重复是指一个处理要施于多个试验单元。完全重复有时也简称为“复制”、“仿行”等。理论上讲，进行试验的目的就是比较不同处理之间是否有显著差异，我们这里是把一个处理所能获得的结果看成一个总体，而实际进行试验时所获得的结果是各个处理所形成的不同总体的抽样。在前面各章（比如第5章介绍的假设检验）告诉我们，显著性检验都是拿不同总体间形成的差别与随机误差相比较，只有当各总体间的差别比随机误差显著地大时，才说“总体间的差别是显著的”，没有随机误差的估计就无法进行任何统计推断。为此，就要在试验的安排中，在处理相同的条件下一定要进行完全重复的试验，以便获得试验误差的估计。需要注意的是：一定要进行不同单元的完全重复（replicate），而不能仅进行同单元的重复取样（repetition）。换言之，一定要重新做试验即完全重复试验，而不能只是重复观测或重复取样。比如在热处理车间，研究什么样的工艺条件（加热温度、加热时间等）能使叶片弹簧的断裂强度达到最高。每次试验要在热油槽中置放100片叶片弹簧，热处理后可以测量出弹簧的断裂强度，一个试验单元指的是一个热油槽。同一个热油槽中不同的叶片弹簧间的差别是各个体间的差异，而我们要讨论的是不同的工艺条件造成的差别，因此这时的“完全重复”指的是，同一种工艺条件要在多个热油槽中进行热处理，而不能仅在同一个热油槽中取出不同的叶片弹簧。显然，同一个热油槽中不同的叶片弹簧间的差异要小，而不同热油槽间差异要大。以同单元重复取样得到的差异估计试验误差将会造成低估，所得的结论就都是不可信的。我们在试验安排中一定要包含真正的重复。当然，完全重复不一定要对所有处理全都重复，下面会介绍一些方法来节省试验次数，例如可以安排只在“中心点”处进行完全重复，别处只进行一次试验，这将大大节省试验费用。

随机化是试验设计的第二个原则。随机化的含义是以完全随机的方式安排各次试验的顺序和／或所用试验单元。这样做的目的是防止那些试验者未知的但可能会对响应变量产生某种系统的影响。仍以热处理试验为例，假使我们要考察热油温度（摄氏度）为700，750，800，850对断裂强度的影响。如果在整个上午按温度由低到高的顺序进行试验，会有什么问题吗？如果当天的电压有一种由高向低变化的趋势，而恰好电压的降低将导致断裂强度的降低，那么很明显，究竟是热油温度的作用还是电压的作用，这是无论如何也分辨不清的。如果将这些试验顺序完全打乱，则不会再出现上述问题。随机化并没有减少试验误差本身，但随机化可以使不可控因素对试验结果的影响随机地分布于各次试验中，因此可以防止未知的但可能会对响应变量产生某种系统影响的出现。

区组化是试验设计的第三个原则。在实际工作中，各试验单元间难免会有某些差异，如果能按某种方式把它们分成组，每组内可以保证差异较小，即它们具有同质齐性（homogeneous），而允许区组间有较大差异，这将使我们可以在很大程度上消除由于较大试验误差所带来的分析上的不利影响。一组同质齐性的试验单元称为一个区组（block），将全部试验单元划分为若干区组的方法称为区组化（blocking）或分区组。通过在同一个区组内比较处理间的差异，就可以使区组效应在各处理效应的比较中得以消除，从而使对整个试验的分析更为有效。例如，假定在白班、夜班时段内差异不大，而白班、夜班差异可能较大，就把白班、夜班当作两个区组。这时在分析中就可以去除掉白班、夜班间差异的影响，或尽可能把试验全都安排在白班（或夜班）进行。如果分区组有效，则这种方法在分析时，可以将区组与区组间的差异分离出来，这样就能大大减少可能存在的未知变量的系统影响。这就是分区组的好处。当然，在区组内还应该用随机化的方法进行试验顺序及试验单元分配的安排。什么时候用分区组，什么时候用随机化呢？在试验设计中应遵照下列原则：“能分区组者则分区组，不能分区组者则随机化”（Block what you can and randomize what you cannot）。

13.1.3　试验设计的类型

根据不同的研究内容，可以对试验设计进行多种方法的分类。

根据试验的因子的个数，可以分为单因子、多因子。根据试验的目的，可以分为因子筛选设计、回归设计。在不考虑区组的设计中，常用的有完全随机化设计（complete randomized design）；在考虑区组的设计中，常用的有：配对比较设计（paired comparison design）、随机区组设计（randomized block design）、平衡不完全区组设计（balanced incomplete block design）、部分平衡不完全区组设计（partial balanced incomplete block design）等。根据因子效应是固定效应还是随机效应可以分为两大类。在固定效应中，又可以分为单向分类（one-way layout）、双向分类（two-way layout）、多向分类（multi-way layout）。在随机效应中，主要是应用嵌套设计（nested design）或称方差分量模型（variance component modeling）。这些试验设计用到的理论和方法都比较复杂，工程师们用得较少，在MINITAB软件中也没有相应的窗口。除了单因子试验设计将在13.2节简单介绍外，别的内容本书就不再介绍了，本章的重点是下列几个能直接使用计算机处理的内容。

根据试验目的而分的主要是两大类：因子筛选设计及回归设计。本章开始的叙述中已经说明，我们进行试验有两个基本目的：一是明确哪些自变量x显著地影响着y；二是找出y与x间的关系式，从而进一步找出自变量x取什么值时将会使y达到最佳值。第一种试验的目的是确定在相当多的自变量中，哪些自变量x并不显著地影响着y，应予以删除；哪些自变量x显著地影响着y，应予以保留。我们称其目的为“因子筛选设计”（screening design）。由于这种试验的目的是针对因子的，因此这种试验设计属于“因子设计”（factorial design），或称“析因设计”或“因析设计”。第二种试验的目的是确定y与x间的关系式，找出y对于x的回归方程。由于这种试验的目的是针对回归关系的，这种试验设计称为“回归设计”（regression design）。

当然，这两类设计也有相通之处：一方面，筛选因子的方法其实也是先建立一个y与x间的简单的线性回归方程，然后根据各项系数的显著性来筛选（详细叙述参见9.3节多元线性回归分析）。这里要注意的是，我们在试验设计中所说的“线性”，已经与通常数学概念中的“线性”有所不同：在“试验设计”中的“线性”指的是在回归方程中除了可以包含各自变量的一次项外，还允许包含有两个或多个自变量的乘积项，例如可以含有x₁x₂，x₁x₂x₃等，而通常的数学概念中的“线性”是不允许包含这些项的。在建立了线性回归方程后，除了可以判断变量是否显著外，对于求最大值或最小值的问题也可以求出最佳值，以及达到此最佳值的自变量的最佳设置（通常在试验区域端点），这在实际工作中也常常是有用的。总之，筛选变量也是通过建立回归方程实现的。另一方面，建立了回归方程，仍然可以在方程中判断是否存在效应不显著的因子，可以删除它们，达到筛选因子的目的。因此，因子设计和回归设计间确有相通之处：它们都要建立回归方程。但因子设计只要线性的，而这里的回归设计指的是二阶的。总的说来，筛选的要求是较粗糙的，试验次数较少；建立回归曲面方程要求就细致多了，试验次数要大增。在因子设计中，又可以按因子水平的个数分为2水平因子设计、3水平因子设计和混合水平因子设计。实践证明：在因子设计中，使用2水平正交试验法，再加若干中心点的设计方法最简单有效，因此本书只介绍2水平的试验设计。再细分，因子设计中又有全因子设计（full factorial design）和部分因子设计（fractional factorial design）两大类，将在本章的13.3和13.4两节中分别加以介绍。对于回归设计，我们也以建立二次回归方程为主要工具，介绍响应曲面方法（response surface methodology，RSM），这部分内容将在13.5节详细介绍。

另一类很重要的试验目的是寻求系统的稳健性（robust）。所谓稳健性，是指系统的抗干扰能力要强，即当系统受到难以控制的因子（或称为“噪声”）的严重影响时，系统输出的变异（variation）要足够小。为做到这一点，我们尽量选择那些使系统对噪声变化不敏感的控制因子的某种水平的组合来达到目的，这就是稳健参数设计（robust parameter design）。在国内，这类设计常称为“田口参数设计方法”。这类问题在六西格玛改进工作中也是有重要意义的，将在13.6节中介绍。

如果讨论的是配方问题，例如在橡胶、造纸、药品生产等行业中，我们研究的是在整个产品中各个分量所占的比率问题，显然，这些比率的总和应该为100％。研究这类问题的试验设计称为“混料设计”（mixture design），将在13.7节中简要介绍。

13.1.4　试验设计的策划与安排

人类认识自然界的过程是个循序渐进的过程。一般是这样的：先根据已有的知识提出某种设想，设计一个试验去验证或否定它，从试验中获得的数据帮助人们验证或修正初始的设想，然后又提出了一个更新更深入的设想，再设计新的试验。这个反复的过程会一直持续下去，直到形成了较为完整的理论结果为止。我们进行试验也是一个学习的过程，不可能一蹴而就。我们不要企图“毕其功于一役”，进行一次试验就结束战斗。一般来说，试验要进行好几批，通常采用下面几个步骤：

1．用部分因子设计进行因子的筛选

最开始，情况不很清楚，考虑到影响响应变量的因子个数可能较多（大于或等于5），这时应在较大的试验范围内，先进行因子的筛选，通常应使用部分实施的因子试验设计法，这样获得的结果可能较为粗糙，但试验次数可以大大节省，筛选的目的能够达成就行了。如果认为部分实施的因子试验费用仍然太昂贵，则可以使用试验次数更少的“Plackett-Burman设计”方法或“均匀设计”等方法筛选因子，“Plackett-Burman设计”方法的详细内容见13.4.4节。

2．用全因子试验设计法对因子效应和交互作用进行全面的分析

当因子的个数被筛选到少于等于5个之后，可以进一步在稍小范围内进行全因子试验设计以获得全部因子效应和交互作用的准确信息，并进一步筛选因子直到因子个数不超过3个。

3．用响应曲面方法（RSM）确定回归关系并求出最优设置

当因子个数不超过3个时，我们就有条件采用更细致的响应曲面设计分析方法，在包含最优点在内的一个较小区域内，对响应变量拟合一个二次曲面函数，从而可以得到试验区域内的最优点，但这种方法通常只对望大或望小特性的响应变量特别有效，因为对于望目特性的响应变量满足望目条件的解通常有无穷多个，响应曲面分析无法提供进一步的选择。

4．用稳健参数设计方法（田口设计）寻求望目特性的最优设置

如果试验目的是寻求望目特性响应的最优解，则最好采用稳健参数设计方法。虽然试验次数比RSM稍多些，但此种方法很有效。

以上所说的当然是典型的步骤，在实际工作中，可能跳过某个环节，也可能在某个步骤上反复进行好几次。总之，要不断地筛选因子，不断调整试验的范围和选择因子试验水平，经过几轮试验后才能最终达到试验的总目标。

13.1.5　试验设计的基本步骤

粗略地说，试验设计包含计划、实施及分析三个阶段。

1．计划阶段

这里又可以分为下面几个步骤：

（1）阐述目标。所有团队成员都要投入讨论，明确目标及要求。究竟是为了筛选因子还是为了找寻关系式？最终要达到什么要求？

（2）选择响应变量。在一个试验中若有多种响应，则要选择起关键作用的且最好是连续型指标作为响应变量。如果只能度量出二元响应（成功、失败），则使分析变得困难得多而且需要大大增加试验次数（详见13.3.4.5节）。

（3）选择因子及水平。用流程图及因果图先列出所有可能对响应变量有影响的因子清单，然后根据数据和各方面的知识及专业经验，也可以借助些工具，比如FMEA等进行细致分析并作初步的筛选。不能确定该删除者就应该保留（“宁多毋漏”）。对于水平的选择也要仔细处理，一般来说，各水平的设置应足够分散，这样效应才能检测出来，但也不要太分散以至于将各种其他的物理因素都包括进来，这会使统计建模和预测变得困难。在实际工作中，选择因子及水平才是真正最关键的工作。

（4）选择试验计划。根据试验目的，选择正确的试验类型，确定区组状况、试验次数，并按随机化原则安排好试验顺序及试验单元的分配，排好计划矩阵（planning matrix）。

2．实施阶段

严格按计划矩阵的安排进行试验，除了记录响应变量的数据，还要详细记录试验过程的所有状况，包括环境（气温、室温、湿度、电压等）、材料、操作员等。试验中的任何非正常数据也应予以记录，以便后来分析时使用。

3．分析阶段

对数据的分析方法应与所应用的设计类型相适应。分析中应包括拟合选定模型、残差诊断、评估模型的适用性并设法改进模型等。当模型最终选定后，要对此模型所给出的结果做必要的分析、解释及推断，从而获得重要因子的最佳设置及响应变量的预测。当认定结果已经基本达到目标后，给出验证试验（confirmation run）的预测值，并做验证试验以验证最佳设置是否真的有效。关于分析阶段的具体方法和所使用的统计工具请参见以后各节的详细叙述。