7.4　多样本均值相等性检验

在实际工作中，常常需要讨论多样本的中心位置的比较问题。我们曾在第5章讨论了单因子方差方法，但是那里要求除了数据相互独立，还要求数据都是正态分布而且各水平间方差相等。如果不能保证正态性，那又该如何解决多样本的中心位置的比较问题？由于获得的数据之状况的不同，我们分三部分来讨论不同的处理方法。7.4.1节将介绍Kruskal-Wallis检验法；7.4.2节将介绍Mood中位数检验法；7.4.3节将讨论在试验设计中包含区组的情况下比较多样本的中心位置的问题，给出Friedman检验法。对于使用这三种不同方法的条件和方法间的相互比较问题，将在具体给出方法的同时予以介绍。

7.4.1　多样本Kruskal-Wallis检验法

如果有多组样本，希望进行中心位置的比较检验，其问题是要检验：

在讨论双样本中心位置的比较问题时，我们在7.2节介绍了用求秩的途径解决问题的Wilcoxon-Mann-Whitney方法。1952年，克鲁斯卡尔（Kruskal）与沃利斯（Wallis）两人将WMW检验方法推广到处理检验多样本的中心位置的比较问题，提出了Kruskal-Wallis检验法。与双样本情况一样，在多组样本情况下，也是先将多组样本数据混合起来，求出各个数值在整个数据集中的秩，再按各组分别求出秩的和，通过比较各组的秩和是否差别很大来判断多样本的中心位置是否有显著差异。

设共有k组样本，第i组样本量为n_i，总样本量N＝n₁＋n₂＋…＋n_k，第i组样本的秩和为R_i，第i组样本的平均秩为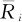，总平均秩是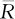。克鲁斯卡尔与沃利斯两人提出H统计量作为各组的平均秩的离差平方和：

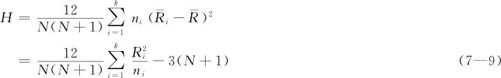
此式的前半部含义很清楚，它相当于不考虑观测值本身，只考虑观测值在全体数据集上的秩值所形成的“组间离差平方和”；而后半部意义不那么明显，但容易计算。这里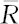是总平均秩，由于所有的样本的所有的秩的总和必为：1＋2＋…＋N＝N（N＋1）/2，此数被N个样本平均，故有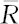＝（N＋1）/2。H统计量越大，表示各组间差异越大，所以，当H很大时应该拒绝原假设。当每组样本量不超过5，组数恰为3时，有专门的表可查（本书略去此表）；当样本量较大且各组样本量所占比率趋于固定常数时，H近似于自由度为k－1的卡方分布；在大样本时，H经简单变换就能近似F分布。对于这些细节大家不必全部了解，只要明白H统计量的含义，知道H越大表明各组差异越大就行了，因为MINITAB会自动算出p值供我们判断使用。在有结的观测值出现时，除了用“平均秩”的方法代替“并列秩”，计算机还将对H值予以修正。过去手工计算时，按Kruskal-Wal-lis检验法的使用说明，只在带有结的观测值太多，以至于超过总观测值个数的25％时，才对H进行修正（参见参考文献［18］第354页）。现在，只要MINITAB输出结果中列出了修正值，我们就应采用修正的结果。

例7—10

某轧钢车间对四种不同供应商提供的原材料轧出来的钢板进行断裂强度测试，各种原材料所抽取样本量不全相等。数据见表7—10（数据文件：NP_四组钢板.MTW）。

表7—10

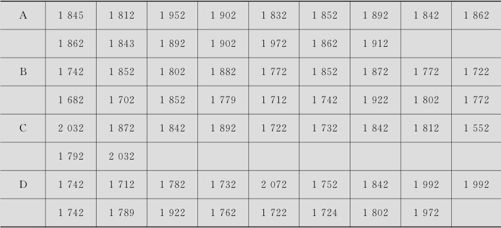
试检验四组不同原料生产的钢板间平均断裂强度间是否有显著差别。取α＝0.05。

解　此问题是要检验：

如果对此问题用单因子方差分析来解决，则必须验证4组数据皆独立、皆正态。但是，在正态性检验时发现对于原材料D，数据并非正态。因此，本问题只能用非参数方法解决。

用MINITAB软件，从“统计＞非参数＞Kruskal-Wallis（Stat＞Nonparametric＞Kruskal-Wallis）”入口（参见图7—7），填写“响应变量（Response）”为“断裂强度”及“因子（Factor）”为“材料”，即可得到下列结果。

Kruskal-Wallis检验：断裂强度与材料

在断裂强度上的Kruskal-Wallis检验

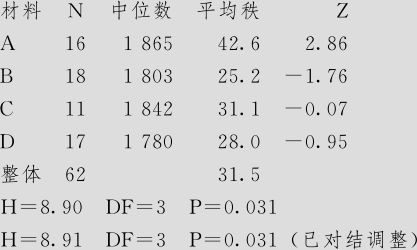
输出结果的前半部是四组材料下断裂强度的样本量、中位数、平均秩及相应的近似正态Z值。后半部给出了H统计量及相应的p值。H的计算是按式（7—9）进行的，数据文件“NP_四组钢板.MTW”中记录了手算的具体过程，最后得到H＝8.90323。本数据集中，共有结值5个（如1712，1803等），含结的观测值共有11个（如1712有2个相同者；1803有3个相同者等），虽未达到总数62的1/4，但我们应该采用MINITAB输出中的最后一行作为最终结果。由于p值＝0.031＜0.05，因此拒绝原假设，即认为四种原料下的钢板断裂强度间确实有显著差别。

Kruskal-Wallis检验法相当于符号秩检验的推广，是相当灵敏的，样本量不必很大，但是此方法容易受到数据中存在的个别异常数据的严重影响。

7.4.2　多样本Mood中位数检验法

对于多组样本中心位置的比较检验还有另一种简便方法，这就是Mood中位数检验法。其主要思想是：先将k组样本数据全部混合起来，求出整个数据集合的中位数M，然后对于各组数据计算出“观测值比M大”的个数和“观测值比M小”的个数；将这些数汇总起来就可以得到一个k行两列的列联表。对于列联表进行卡方检验就可以断言各组的中心位置是否有显著差别了。我们要检验的假设是：

式中，η代表中位数。

例7—11（续例7—10）

某轧钢车间对四种不同供应商提供的原材料轧出来的钢板进行断裂强度测试（数据文件：NP_四组钢板.MTW）。试检验四组不同原料生产的钢板间平均断裂强度间是否有显著差别。取α＝0.05。

解　我们要检验的问题是：

H₀：η₁＝η₂＝…＝η₄

H₁：至少一对η_i≠η_j

用MINITAB软件，从“统计＞非参数＞Mood中位数（Stat＞Nonparametric＞Mood's Median Test）”入口（参见图7—7），填写“响应（Response）”为“断裂强度”及“因子（Factor）”为“材料”，即可得到下列结果：

Mood中位数检验：断裂强度与材料

断裂强度的Mood中位数检验

整体中位数＝1843

将全部62个数据汇总，求出整体中位数是1843。然后看各组中有多少小于等于中位数者，有多少大于中位数者，汇总成表7—11。

表7—11　Mood中位数检验的列联表

用列联表的卡方检验，可得p值＝0.034＜0.05，所以拒绝原假设，即认为四种原料下的钢板断裂强度间确实有显著差别。

一般说来，Mood中位数检验相当于符号检验，比较粗糙，要求样本量也要较大，检验效率比较低，但它对于异常观测值的存在不敏感，有较好的稳健性。

7.4.3　多样本Friedman检验法

我们现在讨论另一种类型的多组样本中心位置的比较检验问题。先看一个例题。

例7—12

某热注塑车间生产手机外壳。对于外壳有多项指标：表面是否光滑、是否有小斑点、是否有毛刺、色泽是否光亮等。测量员凭操作规程中列出的标准给每件外壳打分。现对3件手机外壳由4个测量员为其打分，数据记录如表7—12所示（数据文件：NP_手机外壳.MTW）。

表7—12　手机外壳质量评分表

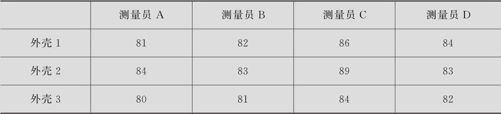
试检验3件外壳评分间是否有显著差异。取α＝0.05。

解　要检验的假设是：

H₀：η₁＝η₂＝…＝η_k

H₁：至少一对η_i≠η_j

粗略看，中位数与平均值都是位置中心的代表，这就是很简单的方差分析问题。按照单因子方差分析方法，将外壳当做唯一的因子就行了。但实际上这样考虑是有问题的，因为测量员之间的差异其实并不是随机误差，测量员自己给被测的几个外壳打分是可比的，而不同的测量员之间很可能有系统差异（例如有人评分总容易偏高些，有人评分总容易偏低些）。这时我们虽然对测量员间打分的规律并不感兴趣，但也不得不考虑测量员之间差异的影响。这类似于双样本的配对检验，但配对检验要求数据正态，而且只限于两个样本，现在推广到多样本，而且不要求数据的正态性。我们把每个测量员当作一个区组（block），即区组内的性质比较一致，但区组间有可能有我们并不感兴趣的系统差异存在。我们感兴趣要比较的是外壳评分，称外壳为“处理”（treatment）。就是要分析处理间差异是否显著。Friedman检验所解决的就是带区组的中位数比较问题。

在进行分析前，先要将数据整理成每个变量自成一列的形式。在堆叠这种数据时，与以前习惯的“按行堆叠”或“按列堆叠”都不同，现在是要把“行名”及“列名”分列在两列中，评分结果再单列一列。

用MINITAB软件，从“数据＞堆叠＞列的区组（Data＞Stack＞Blockin Column）”进入有关界面（见图7—8）。

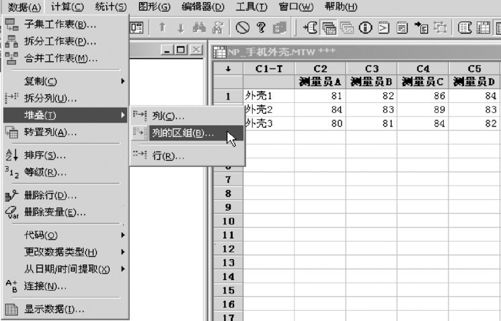
图7—8　带区组数据的堆叠操作1

这时将出现如图7—9所示界面。

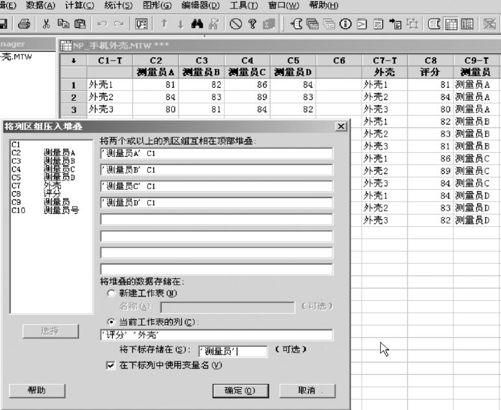
图7—9　带区组数据的堆叠操作2

在要堆叠的各行中，第一行填写“测量员A　C1”；第二行填写“测量员B　C1”；依此类推。在给新列命名时要注意与刚填好的顺序对应，指定“评分”和“外壳”，另用一列来记录下标“测量员”。即可得到图7—9中右侧所显示的数据存放形式。

由于要考虑区组的影响，要先把每个处理（本例是外壳）在区组内（对于同一个测量员）的得分排序求出秩来（评分越低名次越小，因此秩越大表示评分越好。外壳1在4个测量员评分中分别列为2，2，2，3；外壳2在4个测量员评分中分别列为3，3，3，2；外壳3在4个测量员评分中分别列为1，1，1，1），再计算出秩和（外壳1秩和为9；外壳2秩和为11；外壳3秩和为4）。Friedman统计量S的定义是：

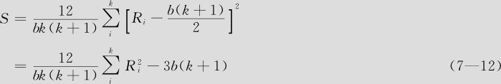
式中，b是区组（测量员）个数；k是处理（外壳）个数；R_i是第i个处理的秩和。由于每个区组内都有秩1＋2＋…＋k＝k（k＋1）/2，b个区组秩和共有bk（k＋1）/2，平分到k个处理上，每个处理的平均秩和为b（k＋1）/2。在式（7—12）的第一式中的右半部分，其含义是明显的，这就是各处理间平均秩的离差平方和，它越大表示处理间差异越大。当b较大时，W＝S/b（k－1）将近似服从k－1个自由度的卡方分布。MINITAB给出了相应的p值，可以供我们判断使用。

在手机外壳例中，我们要检验的问题是：

H₀：η₁＝η₂＝η₃

H₁：至少一对η_i≠η_j

依次选择“统计＞非参数＞Friedman（Stat＞Nonparametric＞Friedman）”，得到下列输出结果及如图7—10所示界面：

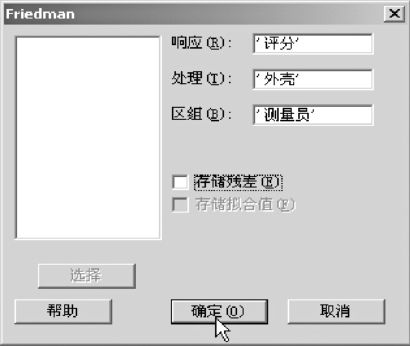
图7—10　Friedman检验信息填写示意图

结果：NP_手机外壳.MTW

Friedman检验：评分与外壳，按测量员划分区组

总中位数＝82.833

由于p值＝0.039＜0.05，因此拒绝原假设，即可以断言，3个手机外壳的评分间有显著差异。

我们可以用散点图画出这种比较的示意。为了画散点图，横坐标不能是属性变量，必须改成数字变量，我们把测量员名称改为1，2，3，4，并列在最后一列。然后选择“图形＞散点图（Graph＞Scatter Plot）”，得到如图7—11所示界面及图7—12。

图7—11　手机外壳评分图操作

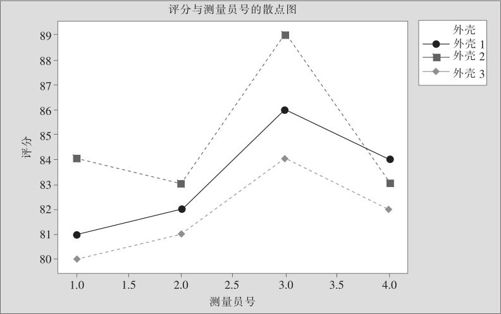
图7—12　手机外壳评分图

如果我们把测量员的差异当作随机误差（不当作区组），就可以使用单因子方差分析。这时的计算结果如下：

单因子方差分析：评分与外壳

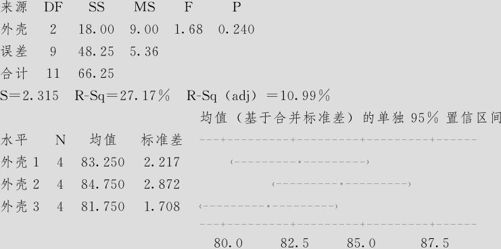
合并标准差＝2.315

由于p值＝0.24＞0.05，因此无法拒绝原假设，即不可以断言3个手机外壳的评分间有显著差异。从箱线图（见图7—13）也看不出3个手机外壳的评分间有显著差异。而实际上评分的差异是存在的。

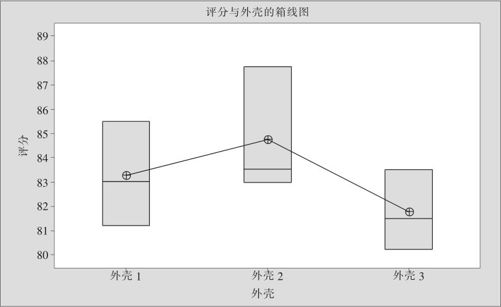
图7—13　手机外壳评分箱线图

这就说明，对于区组效应是不能当作随机误差来看待的。

当然，如果把“外壳”和“测量员”当作双因子进行方差分析是可以得到更准确结论的，但这要求正态性、等方差性等一系列条件。本例中，如果把“外壳”和“测量员”当作双因子，则还必须考虑到二因子的交互作用（详见第10章变异源分析），这就要求要进行重复试验才行，我们的数据不具备此条件。因此可以说，Friedman检验相当于用秩作为数据的方差分析方法。另外，从六西格玛管理的流程来看，应先进行测量系统分析，如果数据说明测量员间有显著差异，先要改进测量系统，然后才能进行下一步的统计分析工作，这些就不在这里详细分析了。