13.2　单因子试验设计

单因子试验在实际工作中是经常会遇到的，它比较简单，但所用到的方法和理论在多因子试验中也会遇到。

单因子试验通常有两个目的：一是想比较一下因子的几个不同设置间是否有显著差异，如果有显著差异，哪个或哪些设置较好；二是建立响应变量与自变量间的回归关系（通常是线性、二次或三次多项式），判断我们建立的回归关系是否有意义。下面就分别介绍这两种要求。

13.2.1　单因子试验设计

我们先举一个实例。

例13—2

在焊接工序中希望比较4种不同烘烤时间所得到的拉拔力是否相等。将20个未焊部件用随机序编好顺序号，再采用随机抽取方法，让4种时间下各选用5个未焊部件，按随机顺序号在烘箱焊接。获得单向分类设计拉拔力数据表（见表13—3，数据文件见DOE_拉拔力（单因子）.MTW）。

表13—3　单因子试验设计拉拔力数据表

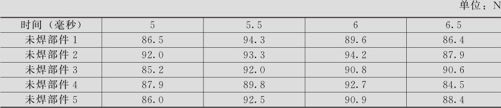
试比较不同的焊接时间是否对焊件的拉拔力有显著影响。

解　本试验是单因子试验，我们只有“时间”这个因子，它取4个水平（即4个不同的焊接时间），这就是单因子试验设计，有时也称作单向分类设计。每个焊接时间进行5次焊接试验，这就是“完全重复”，在安排试验时，采用了随机化方法，将试验单元（每个未焊部件是一个单元）及顺序号两方面皆采用了随机化处理。选取的4个焊接时间是固定的，假定在各固定的焊接时间条件下的焊件的拉拔力之平均值为固定的常数，要比较这些平均值，确定哪个条件下的焊件的拉拔力的平均值最大，各条件下的平均值是否有显著差异等，这是固定效应的问题。因此可以直接采用单因子方差分析法（one way ANOVA）。

在进行单因子方差分析前，先要验证三个前提条件：

（1）各组内数据相互独立；

（2）各组数据皆为正态分布；

（3）各组数据的方差相等。

各组数据较少（每组只有5个数据），独立性可以从宽。正态性容易验证，本处从略。为验证三个前提条件是否成立，也常通过残差诊断来进行。

对于方差相等性，这里要检验的假设是：

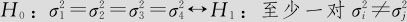
从“统计＞方差分析＞等方差检验（Stat＞ANOVA＞Test for Equal Variances）”入口；在“响应（Response）”处输入“拉拔力”，在“因子（factor）”处输入“焊接时间”，则可以得到图13—4。

图13—4　不同焊接时间的焊接拉拔力等方差检验图

由图13—4所得结果容易看出，Bartlett检验得到p值为0.798，无法拒绝原假设，即可以认为4个总体的方差是相等的。

对于均值的相等性检验，这里要检验的假设是：

H₀：μ₁＝μ₂＝μ₃＝μ₄H₁：至少一对μ_i≠μ_j

使用MINITAB软件，可以从“统计＞方差分析＞单因子（Stat＞ANOVA＞One Way）”入口；在“响应（Response）”处输入“拉拔力”，在“因子（Factor）”处输入“焊接时间”；打开“图形（Graph）”窗，选中“数据箱线图（Data Box Plot）”及“四合一（Fourin One）”，并在“残差与变量（Residual and Variable）”处输入“焊接时间”。打开“比较（Comparision）”窗，选中“Tukey，整体误差率（Tukey，Family Error Rate）”为5％；则计算后可以得到下列结果及箱线图（见图13—5）以及残差图（从略）。由于这些内容在第5章已经作了详细介绍，本处只叙述一些结论。

单因子方差分析：拉拔力与焊接时间

合并标准差＝2.153

Tukey 95％同时置信区间

焊接时间水平间的所有配对比较

单组置信水平＝98.87％

焊接时间＝5.0减自：

焊接

焊接时间＝5.5减自：

焊接

焊接时间＝6.0减自：

焊接

这里要检验的假设是：

H₀：μ₁＝μ₂＝μ₃＝μ₄H₁：至少一对μ_i≠μ_j

由ANOVA结果中可以看出，组内差（随机误差）离差平方和为74.16，自由度为16；组间差（焊接时间差异）离差平方和为101.28，自由度为3，算得F比为7.28，其p值为0.003，显然应拒绝原假设，即应认为不同焊接时间之间的拉拔力有显著差异。

计算中还输出拉拔力的箱线图（见图13—5）。

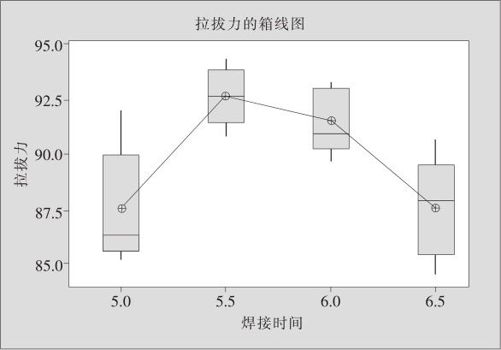
图13—5　不同焊接时间的焊接拉拔力比较图

从图中明显看出，4种不同焊接时间下的拉拔力之间有显著差异。

本例的分析只是方差分析法的一次运用，但我们在安排试验时注意到了试验设计的随机化及完全重复两条原则。实际上，如果不能假定所有20个未焊部件性能基本相同，那就必须再安排划分区组，这里就不再讨论了。

在断言各组间有显著差异后，一个很自然的问题就是要回答：究竟哪些组间有显著差异，而哪些组间没有显著差异？这就要用到多重比较（multiple comparison）的统计方法（见5.5.2节）。

由上述计算结果可以看出，焊接时间在5.5及6.0（毫秒）时拉拔力最大，而且二者间无显著差别；焊接时间在5.0与6.5（毫秒）时拉拔力最小，而且二者间无显著差别；两组间的差异是显著的。从残差的图形中可以看出本数据与方差分析所需三个前提条件符合良好，各残差图皆正常，故本处将残差图略去。

13.2.2　多项式回归

通常单因子试验的第二个目的是希望建立响应变量与因子（自变量）间的回归关系。下面先看一个例子。

例13—3

热处理工序中的油温将影响合金钢丝的弹性模量。试验油温（单位：℃）采用800，820，840，860，热处理后各抽取3根钢丝，将钢丝的弹性模量（单位：N/mm²）记录下来，得到下列数据（见表13—4，数据文件：DOE_弹性（单因子）.MTW）。

表13—4　油温度与弹性模量数据表

试建立弹性模量与温度间的回归方程。

解　由于只有一个自变量，从“统计＞回归＞拟合线图（Stat＞Regression＞Fitted Line Plot）”入口；在“响应（Response）”处输入“弹性模量”，在“预测变量（Predicted Variable）”处输入“温度”；在“回归模型类型（Regression Model）”处选中“线性”；打开“图形（Graph）”窗，选中“四合一（Four in One）”，并在“残差与变量（Residual and Variable）”处输入“温度”。则可以得到图13—6以及残差图（见图13—7及图13—8）。

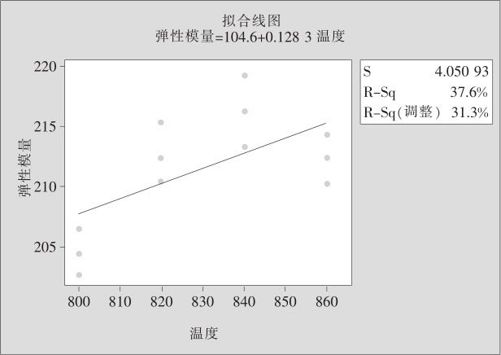
图13—6　热处理油温与弹性模量线性回归关系图

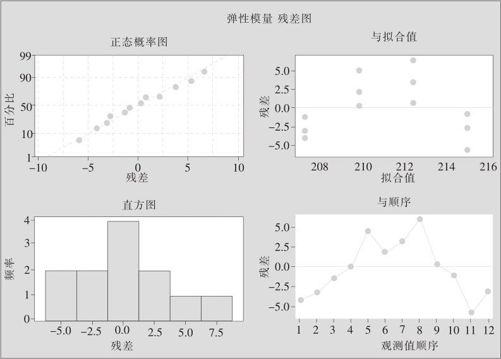
图13—7　弹性模量与油温回归分析四合一残差图

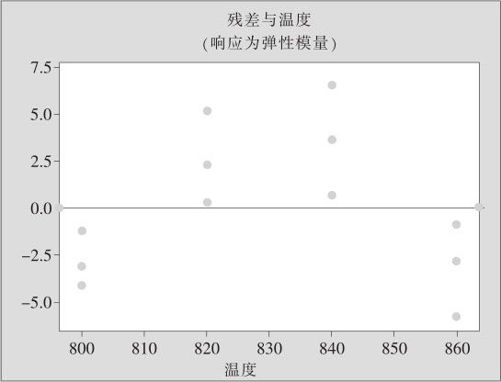
图13—8　弹性模量与油温线性回归分析中对于自变量的残差图

从图13—6及图13—8中可以看出，数据明显有弯曲趋势，应拟合更高阶回归方程。

由于自变量取值已达到3个以上的值，因此可以拟合二次函数，同样从“统计＞回归＞拟合线图（Stat＞Regression＞Fitted Line Plot）”入口，在“回归模型类型（Regression Model）”处选中“二次（Quadratic）”，可得图13—9。

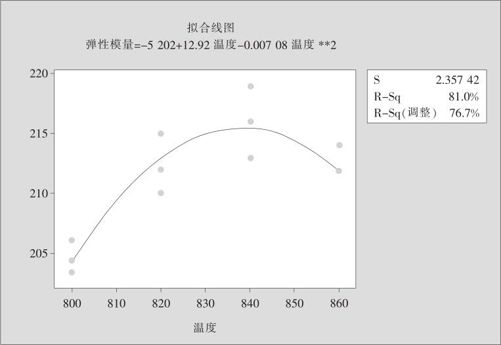
图13—9　热处理油温与弹性模量二次回归关系图

在四合一残差图（此图从略）中看到一切正常，而对自变量的残差图（见图13—10）也无任何有规律性的趋势，因此回归分析可以到此为止（如果图13—10呈现“S”或“反S”形，则要考虑增加为三次回归）。

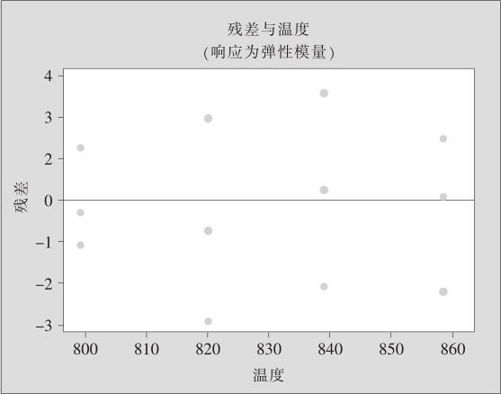
图13—10　弹性模量二次回归分析中对于自变量的残差图

计算结果如下：

多项式回归分析：弹性模量与温度

回归方程为

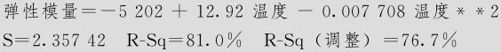
方差分析

方差的序贯分析

先看ANOVA表中的总效果。建立假设检验：

H₀：模型无效H₁：模型有效

本例中，“回归”项的p值为0.001，可见模型是显著的。ANOVA表下方是将回归按“线性”和“二次”分开列出的计算结果，从中可以看到：

线性（Linear）项，p值为0.034，可见线性趋势是显著的。

二次（Quadratic）项，p值为0.001，可见二次项趋势也是显著的。

中学代数中有这样的结论，对于一元二次方程y＝ax²＋bx＋c，若a＞0，则y有极小值，若a＜0，则y有极大值，且极值在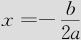处达到。仔细分析本例的回归方程式

弹性模量＝－5202＋12.92温度－0.007708温度**2

可以求出弹性模量的最大点在温度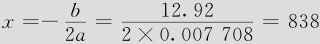处达到。

上述方法还可以推广到更高阶的情形。为了让回归方程中的各项保持独立以便于检查各项效应的显著性，最好选用“正交多项式回归”（orthogonal polynomial regression）。另外，从拟合多项式的阶数上说，一个因子取了k个水平，对于所获得的数据可以拟合一个k－1阶多项式，但实际上，4次以上的多项式一般是不使用的。表面上看，次数增高可以使“拟合效果更好”，但这样的拟合模型缺乏好的预测能力，因为这时估计和预测值的方差都变大了。在回归分析中，称这类现象为“超拟合”（over fitting）。我们应尽量避免这种情形的出现。如果低次多项式与数据确实拟合不好，可以采用“样条回归”（spline regression）或分段样条回归的方法，先将整个区域分为若干小区间，在每个小区间上拟合最高3次多项式，然后将这些多项式拼接修补在一起，形成一个在整个区域上光滑的函数或曲面。这些需要专门的工具，这里就不多介绍了。