3.1　总体与样本

在实际工作中，人们常常关心某个具体问题，我们把所关心的对象的全体称为总体，例如我们关心某公司今年2月生产的螺钉的直径状况，则该公司今年2月生产的全部螺钉就是个总体。当然我们关心的并不是螺钉本身，而是其某个数量特征——直径。而且，当问题的提法发生变化时，所规定的总体也会不同，例如，我们讨论该公司今年一季度生产的螺钉的直径状况，这时总体就是包含前3个月生产的全部螺钉。在总体给定后，我们不可能也不必要研究总体中所包含的全部个体，我们经常会随机地抽取出若干个体作为研究的对象。从总体中所抽取到的这部分个体组成的集合就称为样本。对样本进行分析，目的是了解整个总体的某个统计特性。样本中的个体有时也称为样品，样品的数量称为样本量。

上述说法只是较为粗糙的直观描述。实际上，我们关心的并不是个体本身，而是关心其某个数量特性。由于各个不同个体的数字特性总会有随机波动的状况，也就是说这个数量特性是个可以取不同数值的随机变量，所以，我们应更深入地理解其含义：所谓总体其实就是一个具有确定分布的随机变量，而每个组成总体的个体则是随机变量的一次观测值。

我们最终希望了解的总体特性其实是希望了解总体的分布函数。我们从总体中抽取样本就是为了认识总体的分布函数，希望通过样本数据的分析来推断总体。描述总体数字特征的参数有很多，位置参数有：均值（mean）、中位数（median）、第一（下）四分位数（LQ，Q1或1^st quartile）、第三（上）四分位数（UQ，Q3或3^rd quartile）；散布参数有：方差（variance）、标准差（standard deviation）、四分位间距（inter-quartile range）；形状参数有：偏度（skewness）、峰度（kurtosis）等。对于样本也有相应的统计量，例如样本均值（）等，其详细描述见本章3.2节。我们在这里特别要强调的是区分总体参数与样本相应统计量的差别。例如，我们要弄懂总体均值（μ）与样本均值（）的差别。事实上，当总体指定时，μ一定是个固定的常数，我们称之为参数；样本均值则不然，随着抽样的进行，每次抽样后所得到的结果可能是不同的，它是个随机变量，我们称之为统计量。虽然样本均值通常在总体均值μ周围取值，可以用来估计μ，但这二者是性质完全不同的两个量，我们随时要想到各统计量的随机性，想到它们的不确定性，而且正是由于这种不确定性，导致我们在统计学中总要考虑到在判断上可能犯的错误，或估计中不够精确而产生的误差。我们可以用来估计μ，但绝不能错误地写成二者相等的式子：μ＝，而只能用帽子“^”作为估计量的记号，写成。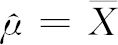

关于总体参数的性质已经在第2章中详细讨论过了，从本章起讨论的就都是针对样本的了。下面一节所介绍的有关性质的分析（例如“均值”）都是针对样本而言的，都是指样本的统计量（例如这里有时把“样本均值”简称为“均值”），读者应特别予以注意。

为了使这种统计推断结果更可靠，还应该注意抽样方法。在较简单的情况下，可以在抽取样本的时候采取随机抽样的方法。采用随机抽样方法形成的样本称为简单随机样本，简称随机样本。真正构成随机样本要具有三个基本条件：

（1）代表性。所抽取的样本一定要能代表所要研究的总体。

（2）随机性。总体中每个个体都有相同的机会进入样本。

（3）独立性。从总体中抽取的每个个体对其他个体的抽取无任何影响。

只有满足上述三项要求的样本才能够很好地反映所研究的总体，大家今后在抽样中要特别注意这些要求。我们今后讨论的样本都被认为是满足这些要求的随机样本。

为了获取随机样本，通常使用不同的随机抽样方法，抽样方法可以粗略地分成几类：

（1）简单随机抽样法。总体中每个个体被抽到的机会是相同的，常用的实现方式可采用抽签、抓阄、查随机数表等。

（2）系统抽样法（等距抽样法、机械抽样法）。随机选取抽样起点后，等距离抽取样本。例如，高考试卷抽样可以规定考生“准考证号末尾两位数字为01者”入选，这就是等间隔的百分之一抽样。要注意的是，如果总体呈现周期性变化，而抽样间隔恰好同这个周期相符合，会导致抽样结果的系统偏差。所以，在已知该总体会发生周期性变化的场合，不宜使用这种抽样方法。

（3）分层抽样法（类型抽样法）。常用于产品质量验收、大规模社会分析等。分层抽样法就是从一个可以分成不同子总体（层）的总体中，按规定的比例从不同层中随机抽取样品的方法。例如，为了调查某城市大学生毕业5年后的平均工资，应先了解他们中分别在国企、合资及外资企业的人数，再了解分别在一般工业、高科技企业、服务业及政府部门工作的人数，按人数比率设定相应抽样量。这种抽样方法将比简单随机抽样有更精确的结果。分层抽样法的优点是样本代表性好，抽样误差小；缺点是实施手续较为烦琐。

（4）整群抽样法。将总体分成群，每个群由个体按一定方式结合而成，然后随机地抽取若干群，并由这些群中的所有个体组成样本。例如，想调查小学生的身体状况，从本市选定三所学校，对这三所学校的所有学生进行数据的采集，这就是整群抽样法。整群抽样法的优点是抽样实施方便，缺点是有可能代表性差。

例3—1

假设有产品微型变压器分别装在100个零件箱中，每箱装20个，共2000个。如果想从中取200个零件组成样本进行测试研究，应如何应用简单随机抽样法、系统抽样法、分层抽样法、整群抽样法这四种抽样方法？

解　（1）简单随机抽样法：将2000个微型变压器编号后混合均匀，抽签或抓阄。

（2）系统抽样法：将2000个微型变压器编号后混合均匀，用抓阄或抽签办法决定起始编号，然后再等距离抽样。

（3）分层抽样法：将箱作为“层”，对100箱，每箱随机抽2个微型变压器。

（4）整群抽样法：先从100箱随机抽取10箱，对这10箱进行全检。

在实际工作中，有时还需要考虑抽样的时间。例如，我们在现场监控某项生产特性指标。这时，所抽取的样本除了要求是随机样本以外，还要求考虑怎样安排抽样间隔。例如，是每10分钟抽1件，还是每小时抽一组5件？我们称5件一组为一个子组（sub-group）。这时，所抽取的样本必须遵循合理子组原则，即子组内差异一定仅由偶然因素引起，因为子组间的差异有可能由异常因素引起。这些将在本书第12章统计过程控制中详细描述。