13.6　稳健参数设计

稳健参数设计（robust parameter design）（也称健壮设计、鲁棒设计，简称参数设计）是工程实际问题中很有价值的统计方法。它通过选择可控因子的水平组合来减少一个系统（或产品、过程）对噪声变化的敏感性，从而达到减少此系统性能波动的目的。大家知道，过程的输入变量（因子）有两类：可控因子（control factor）和噪声因子（noise factor）。可控因子是指其值一旦选定就保持不变的变量，它包括产品或生产过程设计中的设计参数，而噪声因子是在正常条件下难以控制的变量。我们在作参数设计时，就是把可控因子的设置当作研究的主要对象，与此同时让噪声因子按照设定的计划从而系统地改变其水平的方法来表示正常条件下的变化，最终按照我们预定的望大、望小或望目的目标选出最佳设置。从方法角度而言，稳健参数设计可以使用乘积表（cross array）（即内外表“相乘”）和单一表（single array）（两类因子排在同一张表内）两种方法。从建模策略而言，我们可以使用相应的位置—散度分别建模和响应统一建模两种建模策略。田口玄一博士在参数设计方法方面贡献突出，他在设计中引进SN比（信噪比）的概念，并以此作为评价参数组合优劣的一种测度，这是很有价值的，甚至很多文献和软件都把稳健参数设计方法称为田口设计（Taguchi design）。

上述讨论到的响应变量都只限于一个。在我们所研究的系统中，这个响应变量有特定的最佳值（望大、望小或望目），而且这个最佳值是不变的，这类响应称为简单响应（simple response），这类系统称为简单响应系统（simple response system）。在更复杂的系统中，响应变量显著地依赖于一个有效的信号因子，这个系统称为信号—响应系统（signal-response system）。例如，我们研究自动车床生产质量问题，其重要指标就是加工出的零件直径的波动性。如果限定此零件直径是50mm，则可以将其生产工艺条件设计看成是有望目特性的稳健参数设计问题，波动越小越好，这里把生产的零件直径看成是简单响应。但实际上，零件直径是由切削深度决定的，我们可以对切削深度加以控制，不同的切削深度会生产出不同直径的产品。我们希望的是各种直径零件的波动性都能很小。这里，切削深度就是个信号因子（signal factor），整个生产过程就是用切削深度与零件直径间的信号—响应关系来刻画的，仔细研究这种关系将比简单的望目特性研究要深入得多、复杂得多。在田口方法的术语中，简单响应关系被称为是静态（static）特性的，对应的参数设计问题被称为静态参数设计（static parameter design）。信号—响应关系被称为是有动态（dynamic）特性的，对应的参数设计问题被称为动态参数设计（dynamic parameter design）。本书将在13.6.1节讨论一般的稳健参数设计模型，在13.6.2节讨论不含信号因子的静态稳健参数设计的计划问题，在13.6.3节中通过一个具体例题介绍静态稳健参数设计的分析方法，在13.6.4节通过一个具体例题讨论含信号因子的动态稳健参数设计问题。

13.6.1　稳健参数设计的模型

产品性能指标除了受可控因子的影响，还受到噪声因子的影响。一般的试验设计对误差的分析比较笼统，全都归为随机误差或试验误差。但我们在稳健参数设计中，为了能达到产品或过程的稳健性，一定要细致地分析这些变差是如何形成的。首先要明确噪声因子的具体状况，对噪声因子的状况进行细致的分析，然后才能予以准确描述进而设法在试验中反映这些变差，最后讨论如何通过稳健参数设计实现我们相应地控制这些变差的目标。

13.6.1.1　噪声因子的进一步分析

噪声因子就是在正常生产过程或使用条件下难以控制的因子，我们在本章中将不区分“噪声”与“难以控制”。噪声因子可能有很多类型，下面是一些常见的类型。

（1）参数的变化。生产过程中的某些要素，由于在试验设计过程中并不发生设置的改变，我们并未将它们设定为可控因子。但在实际工作中，任何参数的控制都不可能完全准确，这就造成了误差。例如，反应罐中的温度很重要，如果要考虑它们变化产生的影响，则可将它处理为可控因子；否则可以设定为常量，但实际上它是有波动的，因此一般情况下要将温度这个参数的波动看成噪声因子。

（2）原材料参数的变化。加工成产品的零部件有其名义值（nominal value），但是其实际值与名义值总会有偏离，这就造成了变异。由于原材料参数通常被我们选定作为可控因子，这类误差所形成的噪声因子也常被称为“内噪声”（internal noise）。

（3）环境的变化。环境条件对响应变量也会有直接的影响，而我们通常又未将它们放入可控因子范围内，例如手表走时快慢随温度的变化而波动，电视机的清晰度与输入电压的大小有密切关系，很多生产过程与室内条件有关，例如温度（或湿度、静电粒子数、输入电压）等，我们要在参数稳健设计中考虑如何使产品对这些环境的变化不敏感。称这种使用条件和环境条件的波动为外干扰，也称为外噪声（external noise）。

（4）载荷因子。载荷因子是指产品所承受的外部载荷。例如，洗衣机的设计中要考虑洗衣量的变化，汽车设计要考虑载重量的变化，冰箱设计要考虑开门次数的变化等。

（5）单元间差异与空间差异。原料的不同批次、操作工的不同安排、反应炉中不同位置会有不同温度等，这些差异也造成响应变量的波动。

（6）时间差异。时间差异是指一段较短的时间区间内，上下午的差异、同一周内不同的几天产生的差异等。

（7）耗损降级（consume degradation）。在一个长时期内，各种条件的缓慢衰变、元器件老化磨损、生物活性降级、材料耗损导致性能的长期变异。要让系统对此类变异更加不敏感。

本章前几节的试验设计中，一般是靠在单元上或在时间上进行重复试验来估计试验误差的大小，试验的最终目的还是针对响应变量本身（例如望大或望小）。而稳健参数设计则把响应变量的变差作为研究对象，寻找并识别出直接影响性能变差的变量，这比原来的要求深入了一大步，功能也大为扩充。

13.6.1.2　试验与建模的策略

响应变量的变差如何才能减小呢？很自然的想法是，通过减小噪声的变差来实现减小响应变量的变差，但这通常要付出较高的经济代价。稳健参数设计则是更好的一种策略选择。这种策略是通过探索可控因子与噪声因子间的交互作用，从而用改变可控因子的水平组合的办法来减小响应变量的变差。因为可控因子通常易于改变，所以稳健参数设计比直接减小噪声变差更经济、更方便。

我们先举一个简单直观的例子。如果可控因子本身受到噪声的影响而有波动，响应变量与这个可控因子的关系是非线性的，则我们可以选择斜率较小的平坦区域从而使响应变量的变差减小。这样减小变差的方法比直接减小可控因子的噪声波动要便宜得多。其示意图可参见图13—72。一般人们是在系统设计（system design）选择确定了系统的构造之后，把选择参数的最佳设置以求减小响应变量变差的方法称为参数设计（parameter design），再进一步把如何限定可控因子的噪声波动的方法称为容差设计（tolerance design）。

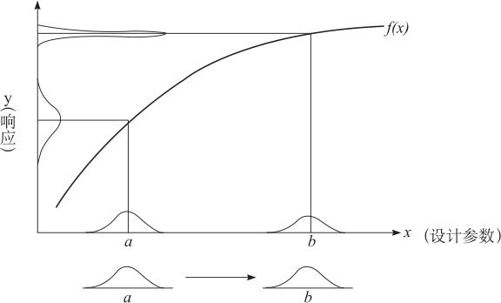
图13—72　选定平坦区域使响应变量变差减小

在稳健参数设计领域，现在公认较好的试验与建模方法有两种不同类型：一种是用乘积表进行位置—散度建模；另一种是用单一表进行响应建模。

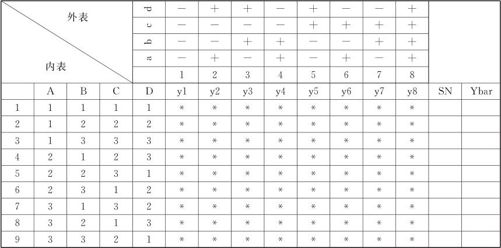
用乘积表进行位置与散度建模：为了考察可控因子的不同水平搭配的效果，我们要在一张控制表（control array）中安排这些可控因子，通常用全因子设计或部分因子设计进行，此表也常称为“内表”（inter array）。为了考察噪声因子的效应，要对控制表中每个试验条件安排一个噪声表（noise array），此表常称为“外表”（outer array）。这样做就相当于控制表中的每个水平组合与噪声表中的所有组合相乘构成一个乘积表（或直积表）。乘积表的示意见表13—36。记n₁和n₂分别为控制表及噪声表的试验次数，则乘积表的试验次数为n＝n₁×n₂。表13—26中的n₁＝9，n₂＝8，表中带“*”的地方表示一次试验，总计要进行72次试验。在田口设计术语中，常将乘积表称为内外表（inter-outer array）。

表13—36　稳健参数设计的乘积表

对乘积表试验的数据该怎样建模和分析呢？一个很自然的想法就是对位置和散度分别建模的方法。

位置—散度建模法（location and dispersion modeling）就是分别建立位置和散度的度量值关于可控因子主效应和交互效应的模型。对每个控制水平的组合，用噪声重复试验的样本均值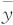作为位置的度量，用样本方差的对数lnS²或样本方差S²本身作为散度的度量。对这两种度量，分别找出对它们有显著影响的因子来。

凡对位置度量有显著影响者，称为位置因子（location factor）；

凡对散度度量有显著影响者，称为散度因子（dispersion factor）；

是位置因子但又非散度因子者，称为调节因子（adjustment factor）。

这三者关系可以参看示意图（见图13—73）。

图13—73　因子分类示意图

对于望目型问题，解决问题的两步程序是：

（1）选择散度因子的水平使散度最小化；

（2）选择调节因子的水平使位置达到目标值。

在第二步中，若只使用一个调节因子仍不足以使位置达到目标值，则可能使用两个或多个调节因子来达到目的。若没有调节因子存在，只能使用同时仍是散度因子的位置因子，这时候，有可能当位置调整到目标时散度却增大了，这就需要重新调整散度因子，并且要在上述两步间进行迭代。如果第二步总也不能使位置达到目标值而且偏差明显时，第一步所得到的结果可能要推翻重来。甚至也有可能仅用这两步法根本就找不到可控因子的最佳水平组合。

对于望大或望小型问题，解决问题的两步程序是：

（1）选择位置因子的水平使位置达到最大（小）；

（2）选择非位置因子的散度因子的水平使散度最小化。

之所以可以使用位置—散度建模法解决稳健参数设计问题，是因为在乘积表中，我们对于位置和散度的度量都是在相同的噪声表中进行的，位置（或散度）度量间的任何差异都可以归因于可控因子水平的组合。因此，乘积表的使用自然会导致使用位置—散度建模法来寻求最优解。

13.6.1.3　位置及散度的度量

取什么指标作为位置及散度的度量是最好的呢？前面所说的样本均值及样本方差是常见的选择，但响应变量优化的目标可能有望大、望小和望目三种形式，统一使用“信噪比”及“灵敏度”是田口提出的建议之一。粗略说来，对于望大、望小和望目三种形式，用不同的公式来定义信噪比后，位置—散度建模法优化步骤的第一步都可以归结为信噪比极大化，第二步再根据不同的目标选不同的因子予以调节，不一定都选“灵敏度”做指标。下面给出不同特性情况下的信噪比（signal to noise ratio，SN ratio）定义。

1．望目特性信噪比

望目特性的SN比与变异系数有着密切的关系。

设望目特性随机变量为y，它的期望值为μ，方差为σ²，目标值为m。对于望目特性y来说，我们希望：

（1）μ＝m；

（2）σ²越小越好。

在概率论中，常用变异系数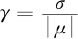作为随机变量的离散性指标，则变异系数γ越小说明随机变量（质量特性）可能值的密集程度越高。变异系数的优点是既考虑了标准差σ的影响，又考虑了期望值μ的影响。如果把标准差理解为绝对误差，则变异系数代表相对误差。

望目特性信噪比定义如下：

可见，望目特性信噪比η等于信号μ²与噪声σ²之比，也就是变异系数平方的倒数。因此，η是随机变量的一个关于变异性的优良指标，其值越大越好。

η的分子μ²的估计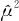由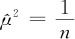（S_m－V_e）确定，分母σ²由

确定，因此有

在实际计算时，通常将估计^η取常用对数再乘以10，化为分贝值。在不致引起混淆的情况下，仍记为η，即

式中

有时更简化为：

另一种信噪比η值的定义是只考虑样本的方差，定义为：

2．望小特性信噪比

当产品的质量特性y为望小特性时，一方面希望其数值越小越好，即等价于希望期望值μ的绝对值或μ²越小越好；另一方面，希望y的波动越小越好，故相当于希望方差σ²越小越好，也就是μ²＋σ²越小越好，其倒数越大越好。因此，望小特性y的SN比定义如下：

注意，随机变量y的2阶原点矩E（Y²）为：

因此

这说明望小特性y的信噪比η应取2阶原点矩E（Y²）的倒数。

2阶原点矩E（Y²）的无偏估计称为均方值V_T：

因此，η的估计公式为：

取常用对数再乘以10，化为分贝值，仍用η来表示，则得到望小特性信噪比的估计公式为：

3．望大特性信噪比

设y为望大特性，则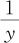为望小特性。因此，将望小特性SN比的估计公式（13—48）中y_i变换成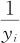，可分别得到望大特性SN比的估计公式：

取常用对数再乘以10，化为分贝值，仍用η来表示，则得到望大特性信噪比的估计公式为：

以上介绍了用乘积表进行位置—散度建模的方法。这是目前最通用的做法，计算机软件也多按此思路编写程序。但是，位置—散度建模方法也有其缺点，这就是用可控因子建立的位置—散度模型可能会掩盖可控因子与噪声因子之间的某些重要关系，因为我们建立的各项效应分析都只考虑了可控因子本身，噪声因子并没有连同可控因子一起予以考虑，特别是未能考虑二者的交互作用。另外，散度还可能并不是可控因子的线性函数，更有可能是其非线性函数，这些使建立度量散度的模型更加困难。再一点就是，乘积表所用的试验次数实在是太多了，因此提出一种全新的设想，即用单一表直接进行响应建模。

在这种响应建模（response modeling）方法中，不是计算噪声因子在重复试验上的方差，而是将响应变量y拟合为可控因子及噪声因子的函数，将这种拟合模型称为响应模型（response model）。安排试验时，也是将可控因子与噪声因子统一排在一张表中，这将大大减少试验次数。其设计及分析用到较多统计知识，本书只好从略。详细内容可以参看本书参考文献［19］：吴建福教授等的著作《试验设计与分析及参数优化》。

13.6.2　静态稳健参数设计的计划

对于实际应用问题，稳健参数设计的主要步骤如下。

1．制定可控因子水平表

同前几节介绍的一般的试验设计一样，首先要确定本问题中的可控因子名单，并确定它们各取多少水平。如果确实需要考虑某些因子间的交互作用，则最好选定所有因子取相同水平的对称正交表（symmetrical orthogonal array），这时交互效应容易得到估计，但水平数受到限制。一般情况下，我们不应特别强调交互作用，可以选用混合水平的非对称正交表（asymmetrical orthogonal array），这使各因子水平数的选择有更多的考虑余地。

2．制定控制表（或称内设计或内表）

一旦可控因子名单和它们的水平确定下来，就可以选定控制表。全部2水平或全部3水平的全因子试验或部分因子试验都可以使用。例如2水平的L4，L8，L16，L32；3水平的L9，L27等。如果有多种水平的混合，则可以选用L18，L36等设计表。在稳健参数设计时，很少使用全因子试验，而多是采用部分实施而且不考虑其交互作用，因为这可以在较少次数的试验中考察相当多的因子，这是很经济和有效的。

使用MINITAB软件可以自动形成内表。主要步骤是：从“统计＞DOE＞田口＞创建田口设计（Stat＞DOE＞Taguchi＞Create Taguchi Design）”入口（其界面见图13—74左），根据自己选定的是对称型（各因子水平数相同）设计还是混合型设计，并考虑到可控因子个数，可以先从“显示可用设计（Display Available Design）”中观察和确认自己选定的试验次数是否可行，然后从对话窗“设计（Design）”中选定试验次数。注意这里的圈选框“为动态特性添加信号因子（Add a signal factor for dynamic characteristics）”是针对动态型稳健参数设计问题而给出的，我们在静态问题中先不要管它。在对话窗“因子（Factor）”中，选定因子名称及水平设置。如果有交互作用需要特别设定的话，注意在这里选择按键“交互作用（Interaction）”后，对要考虑的交互作用项名称予以设定，否则一律不考虑交互作用。全部操作完成后，即可输出设计表（即控制表或称内表）。

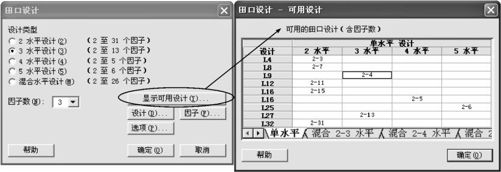
图13—74　田口设计的可用设计表

3．制定误差因子水平表

由于误差因子有很多种类型，要仔细分清每种误差的来源，并设定正确的计算公式。例如，可控因子的误差（用相对误差给出）也是应该作为误差因子来对待的，其取值的计算通常依赖于可控因子本身的数值，而环境误差等则常取固定的设定值作为“外噪声”。

4．制定噪声表（或称外设计或外表）

当误差因子取定后，如何安排噪声表（或称外表）是件非常重要的事。一般情况下，噪声表也采用正交表，因为它可以保证布点“均衡分散”，具有较好的均匀性，这时实施一次噪声表试验相当于在噪声变差范围内实施一次全面模拟试验。而实际上，相当于对内表的每一个试验都要安排一个全面的噪声表。

为了实现对内表的每一个试验都要安排一个全面的噪声表，就要把内表（控制表）和外表（噪声表）“相乘”而得到，相乘的方法如表13—36所示。此表的内表是用L9安排4个可控因子，每个因子皆取3水平。外表是用L8安排4个误差因子，其中每个因子为2水平，按1/2实施安排的。这样一来，搭配在一起共要做9×8＝72次试验。

在用MINITAB软件进行稳健参数设计时，并不真正列出乘积表，误差表（外表）要自己另行安排，其试验结果按顺序填入响应变量的多个列中即可。

能够安排完成全面的乘积表试验当然会得到很好的结果，但噪声因子个数较多或噪声因子水平较多时，试验次数会很大，这时可以用较少次数的试验安排来代替。通常有两种方法可以解决此问题：第一种方法就是综合误差法，考虑在噪声表中选择少数几点（通常3点或4点）能使误差达到最大的最具代表性的试验结果作为全部试验误差的代表，这就可以大大节省试验次数；第二种方法是第一种方法的特例，就是最不利综合误差法，在噪声表中只选2点最不利情况（一个是正偏最不利，另一个是负偏最不利）作为全部试验误差的代表，这就使试验总次数更少了。具体如何选择噪声表要根据实际情况慎重确定。

安排好噪声表后，经过试验，将所有试验结果作为响应变量的多个取值并列排在试验表最右侧，就完成了全部的试验实施及数据收集步骤。

13.6.3　静态稳健参数设计实例分析

下面通过例子说明望目类型问题的稳健参数设计的创建及分析方法。

例13—21

喷塑制成机柜架工艺条件设计问题。喷塑过程的喷入量是喷塑机柜架的关键要求，响应变量是喷入量，其目标值是350克，喷入量过大或过小都将影响机柜架的成型。我们已经知道影响喷入量的因子有4个：喷射压力、喷射时间、喷嘴高度及喷射角度，希望能各取3水平。

因子A：喷射压力，12，15，18（帕）

因子B：喷射时间，4，4.5，5（秒）

因子C：喷嘴高度，1，1.5，2（毫米）

因子D：喷射角，20，22，24（度）

要求分析4个因子效应的显著性，寻求最佳搭配，以使喷入量与目标值350克最为接近。

解　4个可控因子都是3水平，因此选用L9正交表作为可控因子表（内表），其设置代码如表13—37所示。

表13—37　3水平正交表L9

从“统计＞DOE＞田口＞创建田口设计（Stat＞DOE＞Taguchi＞Create Taguchi Design）”入口（其界面见图13—75左）。从对话窗“设计（Design）”中，选定试验次数为“9”（此界面图形从略）。注意这里的圈选框“为动态特征添加信号因子（Add a signal factor for dynamic characteristics）”是针对动态型稳健参数设计问题给出的，在静态问题中，先不要管它。在对话窗“因子（Factor）”中（见图13—75右），选定因子名称及水平设置。全部操作完成后，即可输出设计表，结果见表13—38。

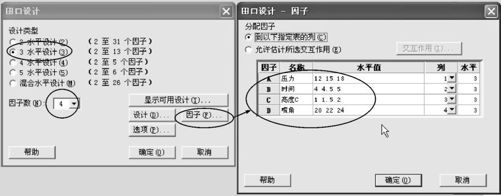
图13—75　田口设计的创建设计操作

表13—38　安排各因子的控制表（内表）

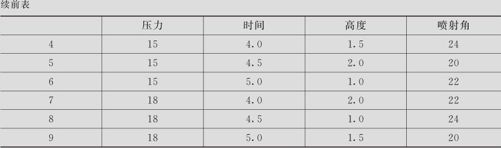
对于误差因子，选定压力（±5％）、时间（±5％）、高度（±10％）及喷射角（±10％）。

用综合误差法，对内表中的每行选取最不利状况（例如每个因子选取上下限的某个边界值）进行2次试验，其喷入量的较大值及较小值分别列在表13—39的C5，C6两列中（数据文件：DOE_喷射量（田口）.MTW）。表中最后两列是计算机自动算出的结果。

表13—39　喷塑试验结果数据表

下面讨论如何使用MINITAB软件进行数据的分析。

计算机软件提供了全部原来要用手工计算的结果，包括信噪比、均值等。用MINITAB软件的操作如下：

从“统计＞DOE＞田口＞分析田口设计（Stat＞DOE＞Taguchi＞Analyze Taguchi Design）”入口（其界面见图13—76左上）。将两列结果（如果有多列，计算方法也相同）都放入“响应数据位于（Response）”内。

从对话窗“分析（Analyze）”、“图形（Graphs）”和“存储（Storage）”中分别选定“信噪比（SN Ratio）”和“均值（Mean）”。在对话窗“项（Terms）”中要选定4个因子名称。

在对话窗“选项（Options）”中要选定信噪比计算公式。由于本例是望目特性，故选用简化信噪比公式（13—42）；也可以单纯考虑样本方差选用式（13—43），本例选定式（13—42）：10Log10（Ybar*2/s2）。也可以选用式（13—38），这时称作“调整后公式”，在图13—76左下部分中，加选“对于望目型使用调整后公式（Use adjusted formula for nominal is best）”项即可。

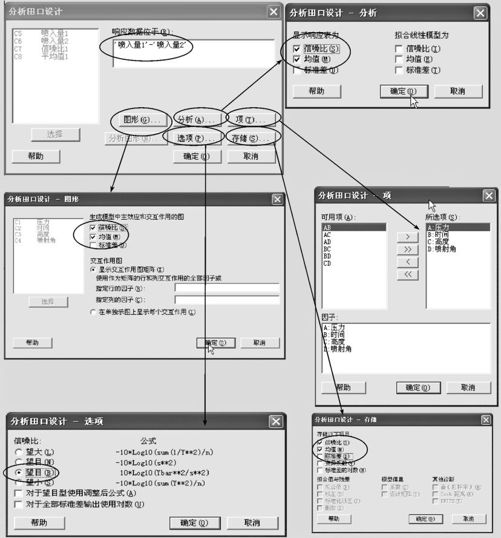
图13—76　田口设计的分析操作

计算结果如下：

田口分析：喷入量1，喷入量2与压力，时间，高度，喷射角

信噪比响应表

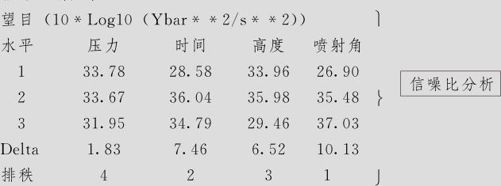
均值响应表

在第一个信噪比响应表内，对于望目特性信噪比（10Log10（Ybar*2/s2））结果的分析，可以看到每个因子的各水平的信噪比平均值和信噪比极差（Delta）。显然，信噪比极差越大代表此因子效应越显著。从极差的大小排秩（Rank）中，可以看出在各因子对于信噪比的影响中，以因子D（喷射角）最为重要（排秩＝1），因子B（时间）次之（排秩＝2），因子C（高度）更次之（排秩＝3），因子A（压力）最小（排秩＝4），几乎没有影响。

在第二个均值响应表内，从均值响应表（Response Table for Means）的分析中，可以看到各因子的各水平均值的平均值和均值的极差（Delta）。从极差的大小排秩（Rank）中，可以看出在各因子对于均值的影响中，以因子A（压力）最为重要（排秩＝1），因子D（喷射角）为次最重要（排秩＝2），因子B（时间）（排秩＝3）和因子C（高度）都很小（排秩＝4），几乎没有影响。

将上述结果归纳一下，我们可以初步判定因子状况：因子D，B，C对望目特性信噪比影响最大，因而为散度因子；因子A，D对均值影响最大，因而都是位置因子；而且由于A是位置因子而又不是散度因子，可以认定因子A为调节因子；D既是散度因子，又是位置因子；最后可以绘制出因子分类的示意图（见图13—77）。

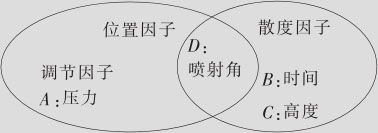
图13—77　田口设计的因子分类表

按望目特性响应变量优化的基本方法，应先选出散度因子的最佳设置，使信噪比达到最大；然后再选调节因子的最佳设置，使均值达到目标。

再来看输出的有关信噪比及均值图形（见图13—78及图13—79），一方面可以确认效应的显著性，另一方面也可以选择最佳设置，以便最后进行预测。

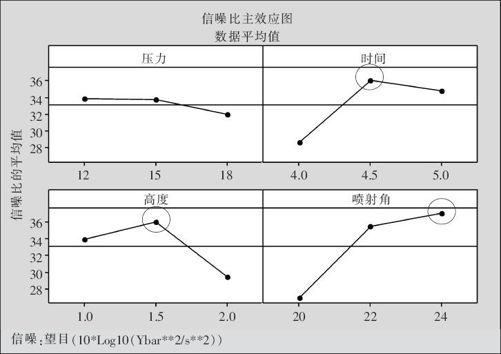
图13—78　田口设计信噪比主效应分析图

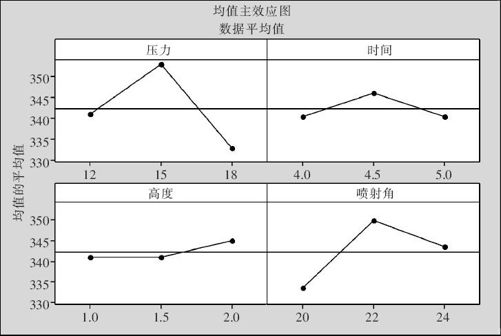
图13—79　田口设计均值主效应分析图

根据对于望目特性的解决问题程序，首先选择散度因子（B，C，D）的水平使信噪比最大化（或说散度最小化）。在本例中，SN最佳水平（见图13—78）应确认为：B（时间）取2水平（4.5秒）、C（高度）取2水平（1.5毫米）、D（喷射角）取3水平（24度），这3个因子的最优设置在图13—78中都用圆圈标出。在这些因子已安排确定的条件下，用调节因子A（压力）的水平进行调试，以使均值与目标最接近。由于3个散度因子的这种最佳搭配并未在试验中出现过，我们只能通过预测来选择。输出时要同时考虑均值及信噪比两项预测。

从“统计＞DOE＞田口＞预测田口结果（Stat＞DOE＞Taguchi＞Predicted Taguchi Result）”入口，其界面见图13—80左。选定预测响应变量为“均值”和“信噪比”。打开“项（Terms）”后（见图13—80右上），选定4个因子。打开“水平（Level）”后（见图13—80右下），选定“从列表中选择水平”后，在各指定因子右方，选择最佳设置，对于调节因子A（压力），逐个选取各水平值（1水平为12帕，2水平为15帕，3水平为18帕），分别得到预测结果，汇总表见表13—40。

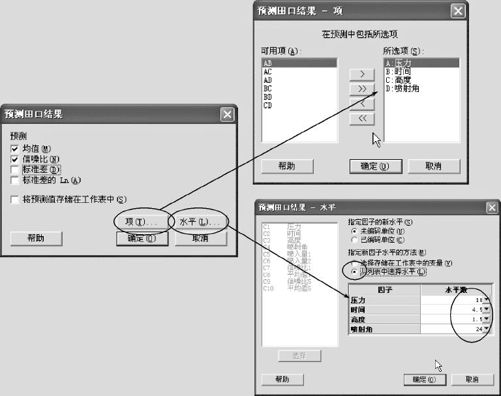
图13—80　田口设计预测结果操作图

表13—40　田口设计预测结果表

从表中可知，在压力取不同值时，信噪比都保持相当好的结果，压力为12帕及15帕时，平均值分别为345克、357克，各自低于及高于目标（350克）。下次试验应取二者中点（13.5帕）附近，预计将会接近目标（350克）。

上述介绍的对于田口试验设计的预测方法，全部是使用主效应迭加方法计算的（因为通常在田口设计中是不考虑交互作用的）。虽然这样预测的结果一般是可信的，但也有很多情况与实际试验结果产生较大偏离，一切都要以验证试验结果为准。为了更深入了解试验观测值与预测结果可能发生偏离的问题以及解决方法，可以参看本书参考文献［11］列出的茆诗松、马逢时和吴建福（1990）的论文。

使用信噪比方法进行稳健参数设计是田口方法的关键环节。但这样做是否总是可行的？多年来批评之声四起。吴建福教授在《试验设计与分析及参数优化》（参考文献［19］）的10.10节中对此进行了深入分析，并且断言：“信噪比方法只在有限范围内有其合理性，而且常常很难用数据证实或者很难在客观背景下得到肯定。”他建议：“在参数优化设计中不推荐使用信噪比方法。如果要将其用于数据分析，则应该补充使用位置—散度建模法及响应建模方法。然后对这三种方法的结果进行比较。如果存在明显不一致，那么信噪比分析的有效性就值得怀疑。”

我们也应该接受吴教授的建议，在使用信噪比方法的同时也按照位置和散度分别建模的方法重复同样的步骤，看看两种方法是否很接近。利用MINITAB软件这是很容易实现的。使用信噪比方法时，选择的指标是“信噪比”及“均值”（参见图13—76的右上、左中及右下），使用位置—散度建模方法时只要换成选择“均值”与“标准差”就可以了。但由于标准差本身性能并不好，应该将样本方差取了对数才好，为此，在选择指标的同时，应该在“选项（Options）”中（参见图13—76左下），增加“对于全部标准差输出使用对数（Use ln（s）for all standard deviation output）”（见图13—81）才行。

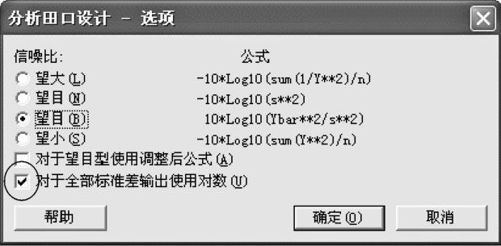
图13—81　田口设计分析补充操作图

这样计算后，本例的输出结果中，替代信噪比分析结果的图13—78，将得到标准差对数的分析图（见图13—82）。其结论及预测结果与使用信噪比完全一致。这说明，在本例中使用信噪比分析还是可行的。当然要注意，直接使用标准差而不用其对数是不好的，预测标准差结果甚至可能得到负值，其最后设置的结果也将与这里给出的略有不同（此处从略）。

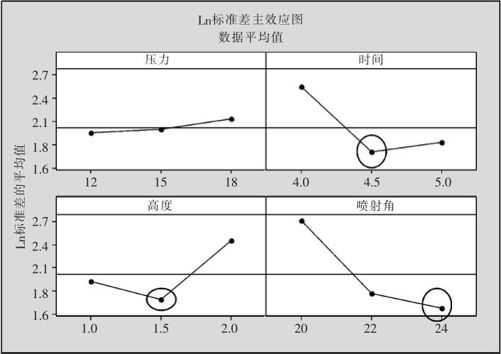
图13—82　田口设计标准差对数主效应分析图

13.6.4　动态稳健参数设计实例分析

13.6.4.1　动态稳健参数设计概念

在13.6.3中介绍的参数设计所讨论的问题是，响应变量为望目特性，我们研究可控因子的设置，使得响应变量的取值与某个固定的目标尽可能接近。但实际工作中的问题常常会更复杂，目标值可以随人们的需求在不同的条件下取不同的值。称固定目标的稳健参数设计为静态（static）的，称这种可以改变目标值的稳健参数设计问题为动态（dynamic）的。下面举几个例子：

（1）车床加工问题。如果要求加工的轴棒直径目标为50mm，我们研究工艺条件设置希望生产出的轴棒直径与50mm越接近越好，这就是简单的静态的望目特性的参数设计问题。事实上，生产过程不可能让轴棒直径目标总固定为50mm，目标可能有多种选择，只要采用不同的切削深度就会导致轴棒直径的变化。我们希望用不同的切削深度生产出来的轴棒直径都能与其相应的目标最接近，这就是动态稳健参数设计问题。把生产轴棒看作一个系统，切削深度为信号因子，轴棒直径是输出特性，我们要研究的问题就是轴棒直径是如何受信号因子切削深度变化的影响的，即研究输出特性如何依赖于信号因子的动态性质。

（2）汽车驾驶中的转向装置。汽车行驶中，常常要变换方向，而这是靠扭转方向盘实现的。方向盘转不同的角度，则车轮会转向不同的方向。我们希望转向系统的设计中，对于方向盘转不同的角度，车轮能有准确的转向。方向盘转动的角度就是信号因子，输出特性是车轮转动方向。

（3）测量系统的设计。在生产日益发展的今天，对测量系统也有越来越多、越来越高的要求，各种物理量都要有相应的测量仪器。我们以数字电子秤为例。将物品放在秤台上，则显示器会显示出物体的真实重量。所称量物体的重量当然是变化的，物体重量是信号因子，输出特性是显示器上的显示结果。

从上述几个简单例子中不难归纳出动态特性的一般性质与要求：在一个系统中，当人发出一个信号后，该系统会产生一个响应值。我们希望研究，该系统应如何设计，以使得响应值与信号间的关系更精确，这就是动态稳健参数设计所研究的问题。

具体来说，动态稳健参数设计问题是：一个系统会受到一些可控因子的影响，也会受到一些非可控因子（噪声、误差）的影响，当该系统接收到某个信号作为其输入特性时，其输出会显示出与之相应的动态特性。我们所要研究的就是，只考虑可控因子的设置，如何选择可控因子的最佳设置以使这种对应关系更准确。

动态稳健参数设计与静态稳健参数设计的差别，其实就是动态多了个信号因子，信号因子可以取不同的值。静态稳健参数设计中没有信号因子。也可以抽象地说，静态稳健参数设计其实就是这个信号因子只取一个固定值罢了，响应也就只有一个固定目标值了。

仔细分析起来，信号因子之中又有两类不同情况，主动型信号因子与被动型信号因子。如果人们能在一定范围内自由取值，则此信号因子为主动型信号因子。例如切削深度、方向盘转角等都是主动型信号因子。如果人们只能被动地取值，则此信号因子为被动型信号因子。例如被测物体的重量，它不是人们自己能控制的，它就是被动型信号因子。

下面我们仔细分析一下动态稳健参数设计将包含哪些内容。

记响应变量为y，可控因子为C，非可控因子为N，信号因子为M，基本模型是：

这里已把噪声因子的影响并入ε项中，ε的均值为0，其方差是固定常数σ²。

动态稳健参数设计的要求就是选定可控因子C的一个最佳水平组合C₀，使得

（1）y的波动（用σ²作代表）尽可能地小。

（2）记m_i为对应于信号因子M取值M_i时所对应的目标值。不论M取哪个值M_i，C₀都能使响应变量y与相应目标m_i的总波动达到最小。

在实际工作中，f（C₀，M）可能是M的各种函数，但非线性函数处理起来太复杂了（如果需要，可以参看吴建福的《试验设计与分析及参数优化》，见参考文献［19］），我们通常只考虑线性函数，一般有下列两种选择：

一般线性关系：

零点比例关系：

在实际工作中，对于模型（13—53），最常见的要求是希望β尽可能地大，也就是说当信号因子M作微小改变时，就能强烈地影响响应变量的值；有时也希望β与某个目标接近。对于模型（13—54），它常用于测量系统设计等领域，最常见的要求是希望β尽可能地接近于1，也就是说当信号因子M改变时，响应变量值的改变尽可能与M相同。

13.6.4.2　动态稳健参数设计的计划

在MINITAB的帮助下，动态稳健参数设计的计划很容易实现。这里首先要明确我们所考虑的因子的不同性质：可控因子、信号因子及噪声因子。在考虑试验计划时，将这些因子的名称、水平数、水平值都设定明确。可控因子的水平尽量取相同数值，例如4个可控因子都取3水平就比较容易安排。信号因子取的水平数则与此无关，可以取任意数值。

安排试验计划的原则是：可控因子及信号因子都安排在内表中，噪声因子安排在外表中。安排可控因子及信号因子时也是分别安排的，如果信号因子取的水平数为k，则相当于将安排可控因子的内表“重复”k次。安排噪声因子的外表，通常不在试验计划中出现，也同静态稳健参数设计一样，可以只选择最不利情况，只进行2次或3次试验就行，数据记录表中也只是并列地给出试验结果就行了。

以下考虑一个实际问题。

例13—22

精密电子秤设计。数字式精密电子秤测量精度要求很高，它由传感器系统、显示系统、稳压系统及恒温系统4部分组成。根据原有经验，这4个系统都各有三种方案可以实施，但希望找到它们之间的最好搭配，以使整个电子秤性能最优。误差因子为环境噪声，包括：环境温度（取18摄氏度、22摄氏度二极端水平）、相对湿度（取25％，70％二极端水平）、网络电压（取180伏、240伏二极端水平）和操作时间（取上午9时、下午15时二极端水平）。为了进行试验，现选择了3个标准砝码：10克、50克及100克，试安排动态稳健参数设计的计划，以选定最佳设计方案。

解　由于这4个系统可以看作4个可控因子，各取3个水平，可以安排在内表L9中。信号因子共3水平，应一起安排在试验计划中。步骤如下：

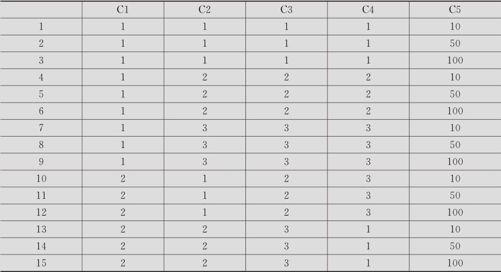
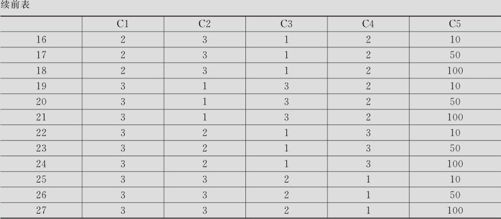
从“统计＞DOE＞田口＞创建田口设计（Stat＞DOE＞Taguchi＞Create Taguchi Design）”入口（其界面见图13—83左）。在对话窗“设计（Design）”中，选定试验次数为9（其界面见图13—83右上）。注意要勾选“为动态特征添加信号因子（Add a signal factor for dynamic characteristics）”。在对话窗“因子（Factor）”中（见图13—83右下），选定因子名称，输入各水平设置，特别注意要在“信号因子（Signal Factor）”内，将信号因子数据列入。全部操作完成后，即可输出设计表（即控制表，或称内表），结果见表13—41。

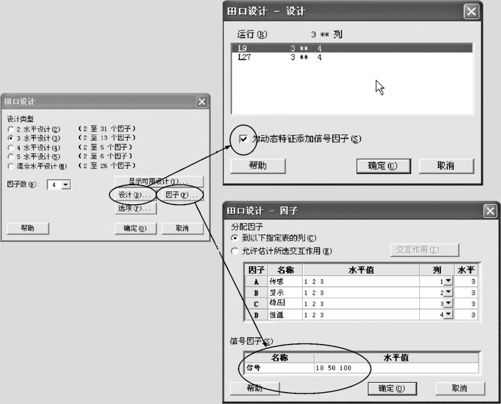
图13—83　动态稳健参数设计计划操作图

表13—41　动态稳健参数设计计划表

对于误差因子，选择综合最不利条件，各自进行2次试验。结果列在表13—42中（数据文件：DOE_电子秤（动态）.MTW）。

表13—42　电子秤设计数据表

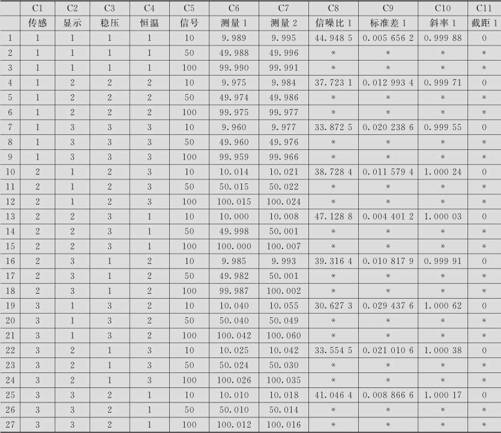
注：此表C1～C7列为观测数据，C8～C11列为计算机计算得出的数据。

13.6.4.3　动态稳健参数设计的分析

由于考虑了三种不同性质的因子：可控因子、信号因子及噪声因子，在分析试验结果时，应该遵照这样的思路来处理：

（1）分析各可控因子的效应，确定哪些因子对信噪比影响显著，选这些因子的最佳水平组合使信噪比达到最大（σ²达到最小）；

（2）确定哪些因子对斜率、截距影响显著而又对信噪比影响不显著（仍可以称调节因子），选这些因子的最佳水平使斜率、截距尽可能达到目标要求。

分析动态稳健参数设计的过程与分析静态稳健参数设计的过程很类似，只是考虑的内容更多些。

下面仍以例13—22的精密电子秤为例，说明动态稳健参数设计的分析步骤。

从“统计＞DOE＞田口＞分析田口设计（Stat＞DOE＞Taguchi＞Analyze Taguchi Design）”入口（其界面见图13—84左上），从对话窗“图形（Graph）”中，选定“信噪比”、“斜率”及“标准差”3项（其界面见图13—84右上）。在对话窗“分析（Analyze）”中（见图13—84左中），选定“信噪比”、“斜率”及“标准差”3项。在对话窗“存储（Storage）”中（见图13—84左下），选定“信噪比”、“斜率”、“截距”及“标准差”（或“标准差对数”）4项。在对话窗“项（Terms）”中（见图13—84右下），选定4个可控因子。

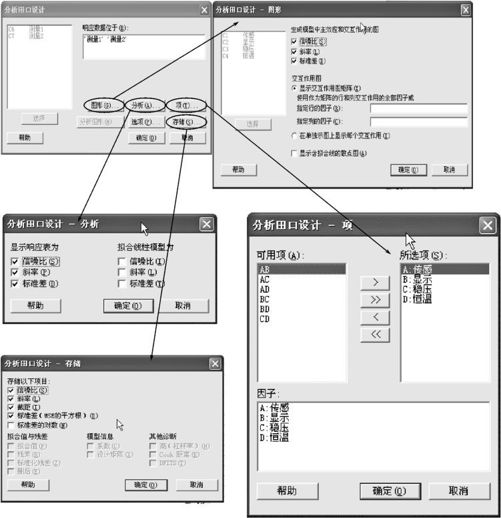
图13—84　动态稳健参数设计分析操作图

上述全部操作完成后，即可输出计算结果如下：

田口分析：测量1，测量2与传感，显示，稳压，恒温

信噪比响应表

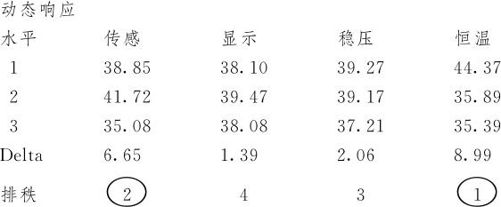
斜率响应表

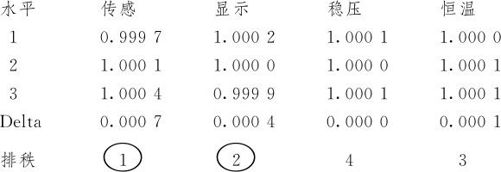
标准差响应表

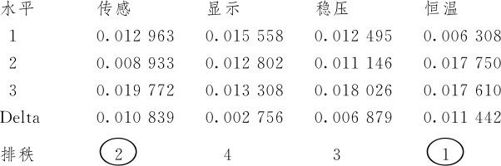
从上述结果可以看出，影响信噪比最显著的是因子D“恒温系统”，次最显著的是因子A“传感系统”，二者都比较显著。影响斜率最显著是因子A“传感系统”，次最显著的是因子B“显示系统”，其他二因子都不显著。从标准差响应表中的分析结果与对信噪比分析的结果相同。按我们解决问题的思路，第一步先寻找A，D二因子的最佳搭配使信噪比最大。考虑上述输出中，D1（信噪比达44.37）与A2（信噪比达41.72）搭配是最佳设置。从信噪比主效应图（参见图13—85左上及右下），也可以证实这一点。

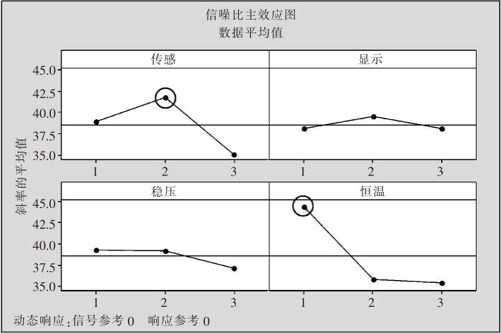
图13—85　动态稳健参数设计信噪比主效应图

第二步是寻求使斜率达到要求的最佳设置。从数值结果分析可以看出，影响斜率最显著因子A“传感系统”取水平2最接近于1，次最显著因子B“显示系统”取水平2最接近于1。从斜率主效应图（参见图13—86左上及右上），也可以证实这一点。

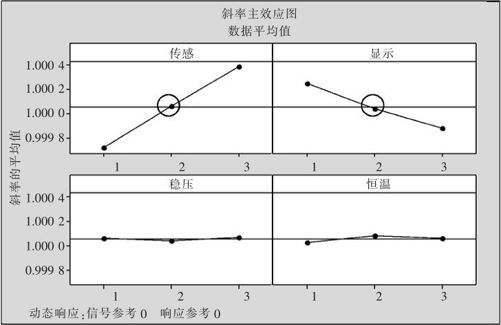
图13—86　动态稳健参数设计斜率主效应图

综合上述结果，可以看出A2B2D1是最佳搭配。因子C效应不显著。为了得到最佳结果的预测，可以利用MINITAB软件直接给出预测结果。

从“统计＞DOE＞田口＞预测田口结果（Stat＞DOE＞Taguchi＞Predicted Taguchi Results）”入口（其界面见图13—87左上），在预测项目上选定：“信噪比”、“斜率”及“标准差”3项；在对话窗“项（Terms）”中（见图13—87右上），选定3个可控因子（删去不显著的因子C）。在对话窗“水平（Level）”中（见图13—87下），选定各因子的最佳搭配。

图13—87　动态稳健参数设计预测操作图

计算后可以得到下列预测结果：

田口分析：测量1，测量2与传感，显示，稳压，恒温

预测值

预测的因子水平

由这些结果可以看出，预测结果相当好，信噪比很大，斜率与1很接近。但我们这里介绍的对于田口试验设计的预测方法，全部是使用主效应迭加方法来计算的（因为通常在田口设计中是不考虑交互作用的），虽然这样预测的结果一般是可信的，但也有很多情况是预测结果与实际试验结果产生较大偏离，这时要以验证试验结果为准。